雙曲型偏微分方程
正文
描述振動或波動現象的一類重要的偏微分方程。它的一個典型特例是波動方程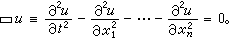 (1)
(1)
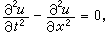 (2)
(2)
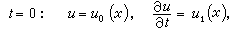 (3)
(3)
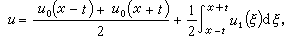
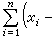
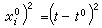 (n=1時為特徵線:x±t=常數)在求解及刻畫解的性質等方面都起著重要的作用。利用二維與三維波動方程柯西問題的解的表達式(泊松公式),可以看到二維與三維的波動在性質上有很大的不同。三維波動的傳播無後效,這對現實世界中信號的傳送與接收有重要的意義,而二維波動卻具有後效現象。
(n=1時為特徵線:x±t=常數)在求解及刻畫解的性質等方面都起著重要的作用。利用二維與三維波動方程柯西問題的解的表達式(泊松公式),可以看到二維與三維的波動在性質上有很大的不同。三維波動的傳播無後效,這對現實世界中信號的傳送與接收有重要的意義,而二維波動卻具有後效現象。 對一般的二階線性偏微分方程
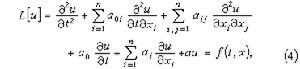 式中係數及右端項ƒ均設為
式中係數及右端項ƒ均設為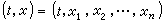 的適當光滑的函式,如果對任一(t,x),由方程(4)的主部所決定的特徵方程
的適當光滑的函式,如果對任一(t,x),由方程(4)的主部所決定的特徵方程 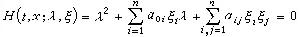 (5)
(5)
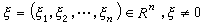 ,
,
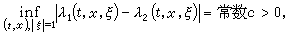
在求解雙曲型方程或研究其解的性質時,特徵超曲面及次特徵線起著重要的作用。一個超曲面S:φ(t,x)=0,如果在其上成立
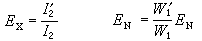 ,就稱它是方程(4)的一個特徵超曲面。對於雙曲型方程,任一特徵超曲面均由次特徵線組成,而次特徵線t=t(τ),x=x(τ)由下述常微分方程組
,就稱它是方程(4)的一個特徵超曲面。對於雙曲型方程,任一特徵超曲面均由次特徵線組成,而次特徵線t=t(τ),x=x(τ)由下述常微分方程組 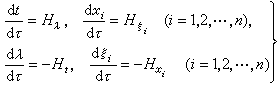
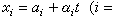
 式中
式中 ,而以p(t0,x0)為頂點的特徵劈錐面就是特徵錐面
,而以p(t0,x0)為頂點的特徵劈錐面就是特徵錐面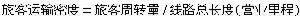 ,此時t軸恰為一個類時曲線。在方程(4)的主部的係數有界時,以任何點為頂點的特徵劈錐面,都可包含在以此點為頂點的一個固定大小的圓錐中。解的弱間斷面一定是特徵超曲面,因此,在波的傳播中,特徵超曲面可用來表示波前,即作為已受擾動與未受擾動的區域的分界面,而任何擾動都沿著次特徵線傳播。這裡,擾動沿次特徵線傳播的性質,充分體現了一般情形下線性偏微分方程的解的奇性傳播的特點。在光學中,次特徵線就是光線,沿著它們積分一些常微分方程,在高頻振動的情況下,可得到精確解的漸近展開式。這一方法稱為幾何光學近似。它將波動光學和幾何光學聯繫起來,並為傅立葉積分運算元提供了一個雛型。
,此時t軸恰為一個類時曲線。在方程(4)的主部的係數有界時,以任何點為頂點的特徵劈錐面,都可包含在以此點為頂點的一個固定大小的圓錐中。解的弱間斷面一定是特徵超曲面,因此,在波的傳播中,特徵超曲面可用來表示波前,即作為已受擾動與未受擾動的區域的分界面,而任何擾動都沿著次特徵線傳播。這裡,擾動沿次特徵線傳播的性質,充分體現了一般情形下線性偏微分方程的解的奇性傳播的特點。在光學中,次特徵線就是光線,沿著它們積分一些常微分方程,在高頻振動的情況下,可得到精確解的漸近展開式。這一方法稱為幾何光學近似。它將波動光學和幾何光學聯繫起來,並為傅立葉積分運算元提供了一個雛型。 對雙曲型方程(4),常見的定解問題是柯西問題或稱初值問題:求方程(4)在t>0時的解u=u(t,x),使它滿足如下的初始條件
t=0: u= u0(x),  (6)
(6)
雙曲型方程柯西問題的現代理論,是由J.(-S.)阿達馬對二階雙曲型方程柯西問題的先驅工作開始的。他通過構造在特徵劈錐面上具有奇性的解(基本解)來求解柯西問題,並採用求發散積分的有限部分的方法來克服所遇到的奇性困難。他的工作經過M.里斯及С.Л.索伯列夫等人的發展,對廣義函式論的建立是一個重要的推動,而阿達馬的方法在廣義函式論的框架中也得到了更清晰和完善的表達。
證明柯西問題適定性的一個比較簡便的方法是能量積分法。所謂能量積分,就是在x空間中由解及其若干階偏導數所組成的正定的積分。在一些常見的波動現象中,利用波在傳播中的能量守恆律,可以知道某些能量積分是不隨時間t變化的常數。對一般的二階雙曲型方程(4),也能在一個包含特徵劈錐面的適當大的圓錐中建立有關能量積分的一些估計式,稱為能量不等式。由此不僅可以證明柯西問題解的惟一性及對初始資料的連續依賴性,還可以證明解的存在性及正規性。為此,自然地採用了泛函分析的框架,並要利用索伯列夫空間的理論。
在一些特殊的情況下,還可以用將解展開為平面波或球面波的方法求得解的表達式。例如對波動方程 (1)帶初始條件t=0: u=0,
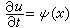 的柯西問題,其解可表為
的柯西問題,其解可表為 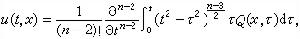
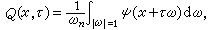
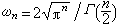 為n維空間中單位球的表面積。由此再通過引入適當的未知函式變換並利用杜阿美方法,對非齊次波動方程帶初始條件 (6)的柯西問題也可以得到相應的解的表達式。
為n維空間中單位球的表面積。由此再通過引入適當的未知函式變換並利用杜阿美方法,對非齊次波動方程帶初始條件 (6)的柯西問題也可以得到相應的解的表達式。 除柯西問題外,另一類重要的定解問題是混合初-邊值問題,簡稱混合問題,即要求方程(4)的一個解 u(t,x),使它在x空間的一個區域的邊界上滿足給定的邊界條件,並在此區域上滿足t=0時的初始條件。在研究波的反射、干擾或有界彈性體的振動等問題時,就會自然地提出這類問題。二階雙曲型方程(4)帶常見邊界條件的混合問題也是在阿達馬意義下適定的。在n=1的情形,對二階雙曲型方程的柯西問題及混合問題都可以利用黎曼函式方法求解。
對於高階的方程或方程組,其雙曲型的定義同樣是和柯西問題的適定性密切聯繫在一起的,甚至可以用保證柯西問題為適定的要求來作為雙曲型的定義。在常係數的情形,已為L.戈爾丁所詳細分析,並給出了此時方程中的係數所應滿足的代數條件,但由於該定義涉及到方程中非主部的係數,難以推廣到變係數的情形。在一般的情況下,有意義的是給出方程中的係數所滿足的一些代數條件,使能保證柯西問題的適定性,並適用於相當廣泛的場合。下面是最常見和重要的兩種情形。
和上述二階雙曲型方程的定義相應,對高階方程
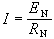
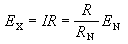
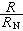
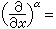
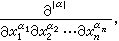 而
而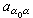 及ƒ適當光滑),若對任一(t,x),由方程主部所決定的特徵方程
及ƒ適當光滑),若對任一(t,x),由方程主部所決定的特徵方程 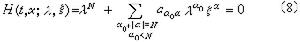
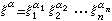 ),對任何
),對任何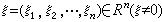 都有N個互異的實特徵根
都有N個互異的實特徵根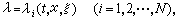 則稱方程(7)為雙曲型方程。如果這N個互異的實根能被一致地分隔開來,即成立
則稱方程(7)為雙曲型方程。如果這N個互異的實根能被一致地分隔開來,即成立 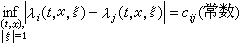
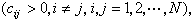
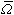 (其中
(其中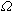 為x空間中的一個區域)上的混合問題,也已得到相當一般性的結果。在上述定義中,實特徵根λj(i=1,2,…,N)互異的假設在套用上往往是過於苛刻的要求。在特徵方程⑻具有重實特徵根的情況,單靠方程的主部一般已不足以保證柯西問題的適定性,而必須考察方程中低階項的影響,情況變得很複雜,是一個正在深入研究的課題。對一階方程組
為x空間中的一個區域)上的混合問題,也已得到相當一般性的結果。在上述定義中,實特徵根λj(i=1,2,…,N)互異的假設在套用上往往是過於苛刻的要求。在特徵方程⑻具有重實特徵根的情況,單靠方程的主部一般已不足以保證柯西問題的適定性,而必須考察方程中低階項的影響,情況變得很複雜,是一個正在深入研究的課題。對一階方程組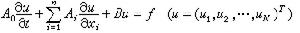 ,(9)
,(9)
對於擬線性及非線性的方程和方程組,其特徵和雙曲型的定義一般要依賴所考察的解,對其柯西問題和混合問題一般只能在t的局部範圍中得到解,而在有限時間內其解可能產生奇性。這一現象稱為解的破裂,在流體力學中對應著新激波的產生等自然現象。然而,在一些特殊而有意義的情形,仍可在大範圍中得到經典解。此外,對非線性波動的周期性及共振等問題,也是重要的研究對象。
在空間維數n=1的情形,特徵超曲面化為特徵線,而與次特徵線重合。此時,可以通過沿特徵線積分的方法來求解雙曲型方程,對它的柯西問題及各種形式的混合問題等,甚至在方程或方程組為擬線性或非線性的情況,都已得到了相當完善的解決。