拿破崙定理

拿破崙定理是拿破崙·波拿巴（Napoleon Bonaparte）提出以任意三角形的三條邊為邊，向外構造三個等邊三角形，則這三個等邊三角形的外接圓中心恰為另一個等邊三角形的頂點的數學定理。

基本信息

• 中文名稱：拿破崙定理
• 外文名：Napoleon's theorem
• 別稱：拿破崙三角形
• 提出者：拿破崙·波拿巴
• 套用學科：數學、歐幾里得幾何
• 適用領域範圍：生活、數學

定理簡介

拿破崙定理

拿破崙十分愛好數學,在數學方面也很有造詣，現提供一個初等數學定理,很有意思。拿破侖定理:三角形ABC中,向三邊分別向外側作正三角形，然後把這三個正三角形的中心連結起來所構成的一定是正三角形，這一定理可以等價描述為：若以任意三角形的各邊為底邊向形外作底角為30°的等腰三角形，則它們的頂點構成一個等邊三角形。

定理推廣

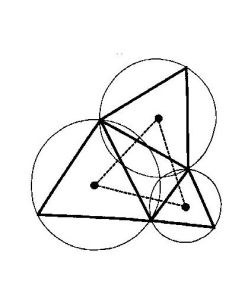拿破崙定理

下面介紹拿破崙定理的兩種推廣：
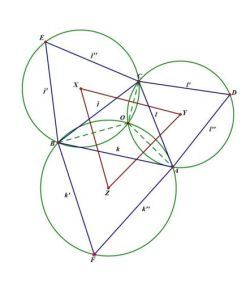
定理1，以△ABC的三邊為底邊各向形外作等腰三角形BCD，CAE和ABF，這三個等腰三角形的底角各為α，β和γ，且α+β+γ＝90°，則∠FDE＝90°-α，∠DEF＝90°-β，∠EFD＝90°-γ．證明 為方便計，把△ABC的三內角簡記為A、B、C．因DC＝DB，則可將△DCE繞D點鏇轉∠BDC至△DBG位置，連FG．
∵∠FBG＝360°-∠DBF-∠DBG
＝360°- (α+β+γ) - (α+C+β)
＝180°-B-C+180°-2(α+β+γ)+β+γ
＝A+β+γ＝∠FAE．
又BG＝CE＝AE，FB＝FA，
∴△FBG≌△FAE，FG＝FE．
從而△DGF≌△DEF，∠FDG＝∠FDE，同理∠DEF＝90°-β，∠EFD＝90°-γ．
定理2，在△ABC的外側作三角形△BCP、△CAQ和△ABR，使∠PBC＝∠QAC＝α，∠PCB＝∠QCA＝β，∠RAB＝∠RBA＝γ，且α+β+γ＝90°，則RQ＝RP，且∠QRP＝2α．
證明 RB繞R逆時針鏇轉2α至RG，連BG、AG、QG．
∵∠GBA＝∠GBR-γ
＝90°-α-γ＝β

又RA＝RB＝RG，即R為△ABG的外心，∴△ABG∽△ACQ∽△BCP，又∠BAC＝∠GAQ，又∠RGQ＝∠AGQ+∠AGR＝∠ABC+α+γ＝∠RBP，∴∠RGQ≌△RBP．∴RQ＝RP．又因∠GRQ＝∠BRP，∴∠QRP＝∠GRB＝2α．
以上摘自百讀拿破崙吧．下面介紹一個更好想的方法：計算法
設新三個三角形的中心分別是Ｏ１　Ｏ２　Ｏ３，
設出角度及邊長，表達出∣Ｏ１Ｏ２∣及∣Ｏ１Ｏ３∣的長.經計算均等於（a2+b2+c2）/6】+(abc/2*√3*R)
其中分別為三邊長，Ｒ為三角形ＡＢＣ外接圓半徑。