射影幾何學內容
在射影幾何學中，把無窮遠點看作是“理想點”。通常的直線再加上一個無窮點就是無窮遠直線，如果一個平面內兩條直線平行，那么這兩條直線就交於這兩條直線共有的無窮遠點。通過同一無窮遠點的所有直線平行。
德國數學家克萊因（圖）在愛爾朗根大學提出著名的《愛爾朗根計畫書》中提出用變換群對幾何學進行分類由於經過同一個無窮遠點的直線都平行，因此中心射影和平行射影兩者就可以統一了。平行射影可以看作是經過無窮遠點的中心投影了。這樣凡是利用中心投影或者平行投影把一個圖形映成另一個圖形的映射，就都可以叫做射影變換了。
射影變換有兩個重要的性質：首先，射影變換使點列變點列，直線變直線，線束變線束，點和直線的結合性是射影變換的不變性；其次，射影變換下，交比不變。交比是射影幾何中重要的概念，用它可以說明兩個平麵點之間的射影對應。
在射影幾何里，把點和直線叫做對偶元素，把“過一點作一直線”和“在一直線上取一點”叫做對偶運算。在兩個圖形中，它們如果都是由點和直線組成，把其中一圖形里的各元素改為它的對偶元素，各運算改為它的對偶運算，結果就得到另一個圖形。這兩個圖形叫做對偶圖形。在一個命題中敘述的內容只是關於點、直線和平面的位置，可把各元素改為它的對偶元素，各運算改為它的對偶運算的時候，結果就得到另一個命題。這兩個命題叫做對偶命題。
這就是射影幾何學所特有的對偶原則。在射影平面上，如果一個命題成立，那么它的對偶命題也成立，這叫做平面對偶原則。同樣，在射影空間裡，如果一個命題成立，那么它的對偶命題也成立，叫做空間對偶原則。研究在射影變換下二次曲線的不變性質，也是射影幾何學的一項重要內容。如果就幾何學內容的多少來說，射影幾何學；仿射幾何學；歐氏幾何學，這就是說歐氏幾何學的內容最豐富，而射影幾何學的內容最貧乏。比如在歐氏幾何學裡可以討論仿射幾何學的對象(如簡比、平行性等)和射影幾何學的對象(如四點的交比等)，反過來，在射影幾何學裡不能討論圖形的仿射性質，而在仿射幾何學裡也不能討論圖形的度量性質。
1872年，德國數學家克萊因在愛爾朗根大學提出著名的《愛爾朗根計畫書》中提出用變換群對幾何學進行分類，就是凡是一種變換，它的全體能組成“群”，就有相應的幾何學，而在每一種幾何學裡，主要研究在相應的變換下的不變數和不變性。
理論
相關書籍同樣，三維歐氏（或仿射）空間中一切無窮遠點的集合叫做無窮遠（平）面。添上無窮遠面後的空間叫做擴d大空間，它也是閉的。在擴大空間，不但平行直線交於一個無窮遠點，而且平行平面交於一條無窮遠直線，一條非無窮遠直線和一個與它平行的平面交於一個無窮遠點。 如果再進一步，把無窮遠元素（點、線、面）和非無窮遠元素平等看待，不加區別，擴大空間就叫做射影空間。同樣，從擴大直線和擴大平面可以得到射影直線和射影平面。在射影空間里，平行的概念消失了：兩條共面直線或一個平面和一條直線總相交於一點，兩個平面總相交於一條直線；此外，每兩點總決定一條直線，每三個不共線點總決定一個平面，等等。
齊次坐標
為了能用代數方法來處理射影(或擴大)空間的幾何問題，需要引進齊次坐標（有時還引進射影坐標）。 仍從歐氏（或仿射）平面開始。設在平面上已經建立了以O為原點的直角（或仿射）坐標系，(x，y)為一點p 的坐標。令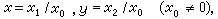
則比值x0:x1:x2完全確定p 的位置，(x0，x1，x2)就叫做p的齊次（笛氏）坐標。原點的齊次坐標顯然可以寫成(1，0，0)。設p不是原點O，則x1，x2不同時等於零；再令x1，x2固定，而令x0向0接近，則p點沿一條經過O而斜率為x2:x1的直線l向遠方移動。設
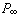表示擴大直線l上的無窮遠點，則可以認為，當x0趨於O 時，p趨於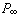。因此，可以把(0，x1，x2)作為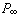的齊次坐標，特殊地，(0，1，0)和(0，0，1)依次是x軸和y 軸上無窮遠點的齊次坐標。這樣，每一組不同時為零的三個數x0，x1，x2 都是擴大平面上一點的齊次坐標，而若ρ 為不等於零的數，則(ρx0，ρx1，ρx2)和(x0，x1，x2)代表同一點，下面引進記號(x)=(x0，x1，x2)，ρ(x)=(ρx0，ρx1，ρx2)。
設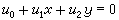
(u1，u2不都是0)是歐氏（或仿射）平面上一條直線的方程。在用齊次坐標表示時，它可以寫成
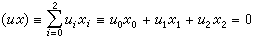， (1)
這也就是擴大直線的齊次方程，這直線上的無窮遠點是(0，u2，-u1)。擴大平面上的無窮遠直線方程顯然可以寫成x0=0。這樣，每一個齊次線性方程都代表擴大平面上一條直線。由於比值u0:u1:u2完全確定直線，(u)=(u0，u1，u2)就叫做（齊次）線坐標。為了區別兩種齊次坐標，上面引進的(x)＝(x0，x1，x2)就叫做（齊次）點坐標。方程(1)叫做點(x)和線(u)的關聯條件或接合（即(x)在(u)上，或(u)經過(x)）條件。 當不區別無窮遠元素和非無窮遠元素，使擴大平面成為射影平面時，(x)和(u)就依次成為射影平面上的齊次點坐標和線坐標，它們都可以看作射影坐標的特款。與此類似，可以得到擴大或射影直線上的點坐標(x)=(x0，x1)以及擴大或射影空間的點坐標(x)=(x0，x1，x2，x3)和面坐標(u)＝(u0，u1，u2，u3)。在擴大或射影空間中，點(x)和面(u)的關聯條件是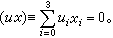
下面，除非特別指明，所討論的空間，就是三維射影空間，所討論的點、線、面都是射影空間裡的點，射影直線和射影平面。在射影空間，指定一個平面x0=0作為無窮遠面，就得到擴大空間（見射影坐標）。
對偶原理
關聯關係是射影平面和射影空間的基本關係。在關聯條件(1)中，(x)和(u)有完全的對稱性，這就使得直線和點可以在邏輯上取得平等的地位。它們叫做平面上的對偶元素。 設方程(1)里的uj是固定的，它就代表一條直線；令滿足(1)的xj變動，就可以得到在該線上的一切點，這些點的集合叫做以(u)為底的點列，而(1)也就是點列的方程。根據線性方程理論，可以看出，點列中每三點線性相關。即：若(y)，(z)是點列中任意兩個不同的點，則它的每一點(x)都可以寫成(y)和(z)的線性組合(x)=λ(y)+μ(z，)，其中λ，μ是齊次參數。在一定意義上，λ，μ也可以作為點列中的射影坐標。另一方面，若令(1)中的xj固定，而令uj變動，就得到一切經過點(x)的直線(u)，它們的集合叫做以(x)為中心的線束，而(1)就是線束的方程，同時也是點(x)的方程。若(υ)，(ω)是線束中任意兩條直線，則線束的每一條直線(u)都可以寫成
。
由於點列和線束中的元素都只依賴於兩個齊次參數的比值，即依賴於一個獨立參數，它們就都叫做一維基本形。 已給平面上一個以點和直線構成的圖形，把其中的點和直線對換，就得到另一個圖形，叫做所給圖形的對偶。例如，點列（和一條直線關聯的點的集合）和線束（和一點關聯的直線的集合）是對偶形。三角形是自對偶形。
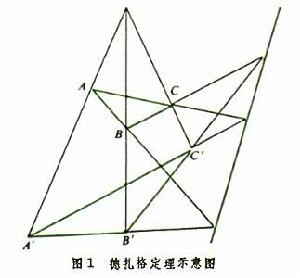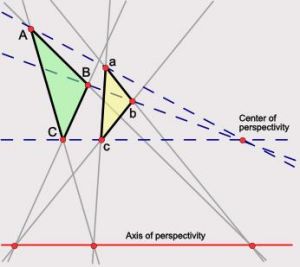
圖1對於平面上一個只涉及點與直線的關聯關係的定理，如果把其中的點和直線及其關聯關係對換，就得到一個新定理，叫做原定理的對偶。“如果原定理成立，則它的對偶定理也成立。”稱它為對偶定理。這是因為，從代數觀點看，這兩個定理的證明步驟是完全相同的。射影幾何中，一個最早而又重要的定理是德扎格定理（圖1）：兩個三角形ABC和
的對應頂點的聯線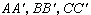
經過同一點的充要條件是它們的對應邊BC和
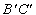；CA和
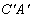；AB和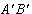
的交點共線。這是個自對偶定理。如果不是在射影（或擴大）平面上而是在歐氏（或仿射）平面上，證明這個定理就需要區別並分別處理其中有某些直線平行的各種特款。
三維空間也有對偶定理。在空間，點和面是對偶元素，直線是自對偶元素。線束是自對偶形。空間還有一個一維基本形是面束，這是經過同一條直線的平面的集合。面束是點列的對偶。在同一個平面上的點的集合叫做點場，經過同一點的平面的集合叫做面把；點場和面把互為對偶。在同一個平面上的直線的集合叫做線場，經過同一點的直線的集合叫做線把；線場和線把互為對偶。點場，線場，面把，線把都是二維基本形。空間的點的集合和空間的平面的集合依次叫做點空間和面空間，它們是互為對偶的三維基本形。在空間，三角形的對偶是三棱形。三棱形由經過同一點的三條不共面的直線所構成，這三條直線兩兩確定三個不共線的平面。對於不共面的兩個三角形，德扎格定理仍然成立，但在空間，它不是自對偶定理。
通過代數來說明對偶原理是簡捷了當的，但不是必須的。 空間的直線構成一個四維集合（見直線幾何）。
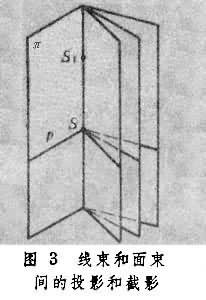
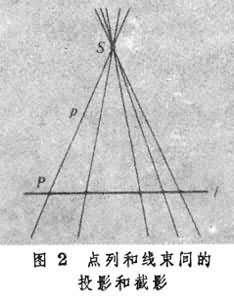
射影對應與射影變換； 在一維基本形之間，可以通過投影和截影互相轉化。 用{p}表示直線l上的點列，其中p表示點列中的任意點。設S為不在l上的一點，作直線p=SP，則當p在l上變動時，就得到以S為中心的線束{p}，叫做點列{p}的投影，而{p}就叫做線束{p}的截影，p和 p叫做對應元素（圖2）。
 |  |
| 圖片3 | 圖片2 |
再設S1為空間不在{p}的平面上的點，作經過S1和p的平面π，就得到以SS1為軸的面束{π}，它是{p}的投影，{p}是{π}的截影，p和π 是對應元素（圖3）。若經過一系列的投影和截影，從一個一維基本形到另一個，這兩個基本形就叫做射影相關，它們元素間的對應關係就叫做射影對應。一個射影對應所包含的兩個變換叫做射影變換，它們互為逆變換。
在空間，通過投影和截影，點場和線把之間，線場和面把之間都可以互相轉化，因而點場之間，線把之間，線場之間，面把之間也可以互相轉化。至於二維基本形之間的其他轉化，例如點場和線場之間的轉化，則可以通過下面將要敘述的代數方法來確定。同樣，三維基本形之間的轉化也要通過代數方法。總之，兩個二維基本形之間或兩個三維基本形之間，也都可以有射影對應和射影變換。
已經指出，如何在點列，點場，點空間，以及線場和面空間裡建立齊次坐標系。事實上，在任何一個一、二、三維的基本形里，都可以建立齊次（或叫射影）坐標（見射影坐標）。這樣，射影對應或射影變換就可以通過齊次坐標間的滿秩齊次線性變換來表示。例如，設(x)，(
)為兩個點場的齊次坐標，則射影變換(x)→()可以用三個變數的齊次線性變換
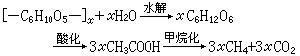(2)
表示，式中det表示行列式；ρ是非零比例常數。解這個方程組，就得到逆變換()→(x)的方程。
射影變換的一個基本性質是保持關聯關係，這等於說，它把線性相關的元素變成線性相關的元素。例如，點場之間的變換(2)就把點列變成點列，即直線變成直線，因而，它還把線束變成線束。由此又可以看出，只涉及關聯關係的每個定理（如德扎格定理）一定代表一種射影性質，即經過射影變換不變的性質。換句話說，這種定理是一個射影定理。
關於射影對應，有一個基本定理。如果把一、二、三維的情況概括在一起，那就是：若在兩個n維 (n=1，2，3)基本形中，分別指定一組n+2個元素，式中各組裡的每n+1個元素線性無關，則兩個基本形間，有惟一的射影對應，使兩組元素按給定次序相對應。事實上，對於任意維射影對應，這個定理都成立。所謂“線性無關”，可以舉例來說明：兩個線性無關的點不重合，三個線性無關的點不共線，四個線性無關的點不共面。 射影變換也可以作用於擴大空間，但經過射影變換，無窮遠元素可以變為非無窮遠，非無窮遠元素可以變為無窮遠（例如平行平面可以變得不平行，不平行平面可以變得平行），因此，在未經擴大的歐氏或仿射空間里，射影變換不完全是一對一的。交比； 交比是一項基本的射影不變數。
根據關於射影對應的基本定理，一維基本形（例如，點列）間的一個射影對應是由三對對應元素惟一地確定的。由此可以推知，若在一個射影對應中，一個一維基本形中的四個元素E1，E2，E3，E4依次對應於另一個一維基本形中的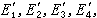 
則四元素組E1，E2，E3，E4和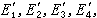必有某種共性。交比就是這樣的共性。
設在一個一維基本形中，元素Ej(i=1，2，3，4)的齊次坐標是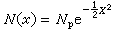
，而用(Ej，Ej)表示行列式
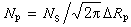
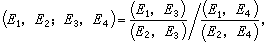(3)
若在一個一維基本形中，隨意選取三個不同的固定元素E1，E2，E3，而對於任意元素p，設
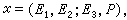
則p 的位置和x 的一切值（包括∞）一一對應。特殊地，當p=E1時，x=∞；p=E2時，x=0；p=E3時，x=1。因此， x可以作為基本形中的非齊次坐標。若再令 x=x1/x0，則(x0，x1)是基本形中的齊次坐標，稱為射影坐標。特殊地， E1，E2，E3的坐標依次是(0，1)，(1，0)和(1，1)。這三個元素叫做射影坐標系的基元素。
在歐氏空間，若p1，p2，p3，p4是四個共線點，而用pjpj表示由pj到pj的有向線段長，則
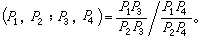
四個元素有24種排列法，但對於一般位置的四個元素只有 6個不同的交比值，對於某種特殊位置的四個元素，則六個交比值中至少有兩個相等。例如，當交比(E1，E2，E3，E4)=-1時，這四個元素稱為構成調和組。這時E1和E2，E3和E4都可以對調，元素偶E1，E2和E3，E4也可以對調，而交比不變；而且元素的其他次序所對應的交比值都是2或1/2。這表明，對於構成調和組的四個元素，變動其排列次序，只有3個不同的交比值，即－1， 2， 1/2。當然，在射影相關的基本形中，調和組對應於調和組。
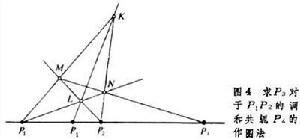圖4在調和組E1，E2，E3，E4里，E4也叫做E3對於E1，E2的共軛；已給E1，E2和E3，可以用直尺作圖求E4。圖4表示，已給點列中任意三點p1，p2和p3，求p3對於p1，p2的調和共軛p4的作圖法。注意K，L可以是經過p3的任意直線上的任意兩點。還可以看出， 當p3趨於p2（或p1）時，p4也趨於p2（或p1）。因此，調和組中可以有三點重合。
直射變換與對射變換，射影群； 考慮一個平面上的二維射影變換。平面既是點場的底，又是線場的底，因此，它上面的一個射影變換可以把點變成點（或線變成線），也可以把點變成線（或線變成點），前一種叫做直射變換，後一種叫做對射變換。
直射變換的逆變換和它們的積（即兩個直射變換接連作用所形成的變換）都是直射變換。因此，平面上一切直射變換構成群，叫做平面直射群。直射變換的特徵是，它把共線的點變成共線的點，因而可以說，也把直線變成直線。一個直射變換可以用關於點坐標的線性變換(2)代表。如果它把直線(u)變成(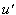
)，則通過關聯條件可得
(4)
式中Cij是сij在方陣(сij)中的余因子，σ是比例常數。可以認為，(2)和(4)代表著同一個直射變換，它們的區別只是在於：一個用了點坐標，一個用了線坐標。
與此類似，對射變換把共點的直線變成共線的點，把共線的點變成共點的直線，即把線變成點，把點變成線。兩個對射變換之積是一個直射變換。對射變換不構成群，但是平面上一切直射變換和對射變換在一起構成群，叫做射影群。直射群是射影群的子群。但有時射影群這個名詞也用來指直射群。 由於平面對射變換把點變成線，把線變成點，而又保持關聯關係，它就體現了平面上的對偶原理。同樣，空間也有直射變換和對射變換，前者把點變成點，面變成面，後者把點變成面，面變成點；它們都把直線變成直線。空間一切直射變換構成直射群，一切直射變換和對射變換構成射影群。空間對射變換體現空間對偶原理。
直線上的一切點變點的射影變換構成直線上的射影群。 其他基本形里都有各自的射影群。
二次曲線與二次曲面； 擴大平面上的二次曲線
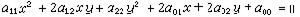
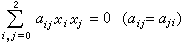(5)
式中αij=αjj表明(αij)是對稱方陣。
在射影平面上，方程(5)所確定的點的軌跡就叫做一條二次曲線。與此相對偶，含線坐標的齊二次方程
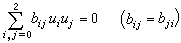(6)
代表一個直線的集合，也叫做二次曲線。為了區別(5)和(6)，它們所代表的點集和線集依次就叫做點（素）二次曲線和線（素）二次曲線。
用Г表示點二次曲線（5），並假定它是滿秩的， 即det(αij)≠0。在它上面的一點(y)，Г的切線方程是
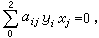
這些切線構成線二次曲線
，式中Aij是αij在方陣(αij)里的余因子。按照對偶原理，點曲線的切線的對偶是線曲線的切點（兩條“相鄰”直線交點的極限位置），因而滿秩線二次曲線的切點構成一個點二次曲線。
設p為不在滿秩點二次曲線Γ上的任意點，經過p作直線l交Г於p1， p2兩點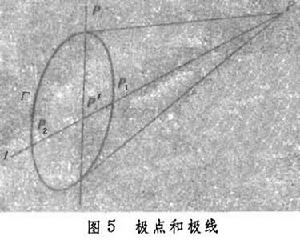（圖5
圖5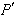
，即(p1，p2；p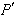，)=-1。這樣的兩點p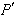，叫做對於Г的共軛點。當p固定而令l轉動時，p的共軛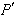總是在一條直線p上，叫做p點對於Г的極線，而p就叫做直線p對於Г的極點。特殊地，若p為Г上的點，它的極線p就是Г在p的切線。顯然，若p的極線經過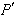，則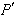的極線經過p。若p和p的齊次坐標依次為(x)和(u)，則 
(7)
這是一種特殊的對射對應，其特殊性在於(αij)是對稱方陣，它叫做對於Γ的配極對應。配極變換的平方，即它和自己的乘積是麼變換（或叫恆等變換）。配極對應也可以體現對偶原理。
二次曲線可以通過射影產生法產生。若在平面上有兩個射影相關的線束（即線束間建立了一宗射影對應），它們有不同的中心，而且它們的公共直線不對應於自己，則兩線束中對應直線交點的軌跡是一條滿秩點二次曲線。用對偶方法可以產生線二次曲線。
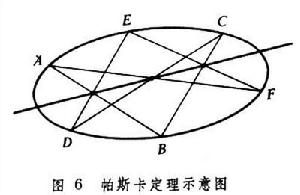圖6射影幾何中，關於二次曲線一個最早的著名定理是帕斯卡定理（圖6）滿秩二次曲線的一個內接六邊形ABCDEF的三對對邊AB和DE，BC和EF，CD和FA交於一條直線上。倒轉來，若一個六邊形的三對對邊交點在一條直線上，則六邊形頂點在一個二次曲線上，但這個二次曲線可能退化成直線偶。帕斯卡定理在平面上的對偶叫做布里昂雄定理。
帕斯卡定理的一個特款是帕普斯定理：若A，B，C 和A┡，B┡，C┡分別是兩條直線上的三點，它們都不重合，則BC┡和B┡C，CA┡和C┡A，AB┡和A┡B交於共線的三點。 在三維射影空間，設(x)，(u)依次為齊次點坐標和面坐標，則含xj的一個齊二次方程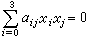
代表一個點（素）二次曲面，而含uj的一個齊二次方程代表一個面（素）二次曲面。滿秩點二次曲面的切面構成一個滿秩面二次曲面，而滿秩面二次曲面的切點構成一個滿秩點二次曲面。
關於滿秩二次曲面也有配極對應，它使極點和極面互相對應，是空間的特殊對射對應。 直紋二次曲面也可以通過射影產生法產生。若兩個射影相關的面束的軸是相錯（即不共面）直線，則它們對應平面的交線構成一個直紋二次曲面的一族母線。 射影幾何的子幾何； 射影群中有許多重要子群，對應於每一個這樣的子群有一種幾何，叫做射影幾何的子幾何。 為了簡單明確起見，下面所說的射影群就是直射群，所說的射影變換是指直射變換，而且主要分析平面上的情況。 在擴大仿射平面上，令無窮遠線x0=0不變的射影變換是仿射變換，用非齊次坐標表示，仿射變換的方程可以寫成
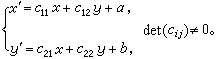(8)
一切仿射變換所構成的仿射群，是射影群的一個子群。仿射變換保持平行性。 在擴大仿射平面的無窮遠線x0=0上，取兩個共軛虛點I1(0，1，i)，I2(0，1，-i)，式中i2=-1。令點偶I1，I2（即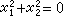
，x0＝0）不變的仿射變換叫做相似變換；它們的方程可以寫成 (8)的形狀，但其中(сij)是正交方陣乘以一個常數:
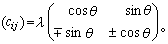一切相似變換構成相似群（也叫歐氏群或度量群），它是仿射群的子群，也是射影群的子群。有了I1，I2兩點後，就可以通過射影方法在平面上引進距離和角的概念（見絕對形），相似變換把每個圖形變成一個和它相似的圖形，即一切長度按比例變化而角不變。這時擴大平面就可以叫做擴大歐氏平面，它上面的一切圓都經過I1，I2。這兩點就叫做無窮遠圓點。
在相似變換中，係數сij構成正交方陣 (即λ＝±1)的，叫做全等變換（或運動）；式中det(сij)＝1的叫做正常運動，det(сij)=-1的叫做反常運動。後者是一個正常運動和一個對直線反射之積。全等變換把每個圖形變成一個和原圖全等的圖形。全等變換群（或運動群）是射影群、仿射群和相似群的子群。
已給一個空間S 以及作用於它上面的變換所構成的一個群G，就可以判斷，在S里，哪些圖形性質經過G中的變換不變，研究這些性質的幾何就叫做屬於G的幾何。若G1是G的子群，屬於G1的幾何就叫做屬於G的幾何的子幾何。射影幾何和仿射幾何依次屬於射影群和仿射群，而歐氏幾何則可以認為屬於相似群，但又部分地屬於全等群；因為它既研究相似圖形，又研究全等圖形。歐氏幾何是仿射幾何的子幾何，它和仿射幾何又都是射影幾何的子幾何；由於它研究圖形的度量性質(長度、角度、面積、……)，它也叫做度量幾何。
群越大，不變性質越少而越帶普遍性；群越小，不變性質越多而越豐富具體。這樣，就可以通過不同的群之間的關係來理解不同的幾何之間的關係。
空間S的圖形還可以通過變換群G分類：把一切可以經過G的變換互相轉化的圖形歸入同一個等價類。例如，一切滿秩實跡（即有實點的）二次曲線都互相射影等價，即屬於同一個射影類，它們卻分為三個仿射類：和無窮遠線不相交（於實點）的是橢圓，相切的是拋物線，相交於兩（個實）點的是雙曲線。每一個仿射類里的二次曲線又可以分為無數度量類；例如同是橢圓，兩個半軸長比值不同的就不相似，半軸長不分別相等的就不全等。
兩種非歐幾何，即橢圓幾何和雙曲幾何都是射影幾何的子幾何。在射影平面上，把虛跡二次曲線
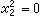變為自己的一切射影變換構成射影群的一個子群，叫做橢圓（運動）群；屬於它的幾何就是橢圓幾何，附有那個不變二次曲線的射影平面叫做橢圓平面。另一方面，把實跡二次曲線
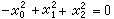變為自己，並把它的內部（即
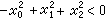的點的集合）變為內部的射影變換也構成射影群的一個子群，叫做雙曲（運動）群；屬於它的幾何就是雙曲幾何；那個二次曲線內部就是雙曲平面。非歐平面上的長度和角度概念也可以通過射影方法來引進。
射影幾何另外一個重要子幾何是閔科夫斯基幾何。把點偶(0，1，1)和(0，1，-1)（即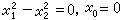
）變為自己的一切射影變換構成洛倫茲群，屬於它的幾何就是閔科夫斯基幾何。閔科夫斯基幾何為狹義相對論提供了天然的幾何說明；四維閔科夫斯基幾何就是四維時空(見閔科夫斯基空間)。 上面所論的射影群的每個子群都有一個不變的圖形（其中有些是虛跡圖形），如對於仿射群的x0=0，對於相似群的
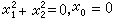，對於橢圓群的
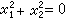等。這種不變圖形就叫做相應子幾何的絕對形。
以上理論都可以推廣到三維以至任意維空間。在三維空間，歐氏幾何的絕對形是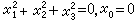
，它叫做無窮遠虛圓；因為擴大歐氏平面的一切球面都經過它。空間橢圓幾何，雙曲幾何和閔科夫斯基幾何的絕對形依次是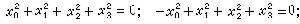
。
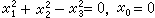公理系統
射影幾何建立在歐氏空間的基礎上，這不是必要的。它可以建立在不涉及度量概念的公理系統上。 以三維射影幾何為例，在那裡，基本元素是點，直線和平面。射影幾何公理的表達形式是多種多樣的，一般可以分為三組。第一組叫做關聯公理：例如，兩點確定一條經過它們的直線，三個不共線點確定一個經過它們的平面，兩個平面交於一條直線等等。第二組叫做次序公理：例如，已給直線上三點A，B，C，直線上必有一點D，使A，B和C，D互相隔離等等。第三組只含一個公理，即連續公理。射影直線上的連續公理實質上就是規定：去掉直線上一點以後，直線上剩下來的部分滿足實數軸上的戴德金連續公理。
根據這些公理，便可以通過純演繹方法建立起一個完整的實射影幾何體系，包括射影坐標。所謂實射影幾何，就是上面所討論的射影幾何，其中點的坐標是實數。 不同維的射影空間，可以在關聯公理里加以區別。 只滿足關聯公理的空間可以稱為一般射影空間；在那裡面，仍然有射影變換，其相應的幾何可以稱為一般射影幾何。如果把關聯公理要求降低，也可以得到更一般的射影空間和射影幾何。當然，在一個一般射影空間裡，實射影幾何的定理不完全成立。 也可以一開始就通過代數方法來建立射影幾何。仍以實三維空間為例，構想每一個非零四實數組(x0，x1，x2，x3)為一點，成比例的四數組代表同一點；再假定線性相關的三點屬於同一條直線，線性相關的四點屬於同一個平面。這樣就把實射影幾何完全建立在實數域的基礎上了。
用n+1數組代替四數組來表示點，就得到n維射影空間及其射影幾何。 若令n+1數組(x0，x1，…，xn)里的xj屬於某一個數域F，所得到的是一個一般射影幾何。例如當F是複數域時，次序公理和連續公理都不能滿足，得到的是很重要的復射影幾何。上面從（實）仿射空間得到（實）歐氏空間時，就曾經利用了虛點I1，I2。 若F是一個有限域，所得到的一般射影空間只有有盡多個點，叫做有盡射影空間。例如，若F是特徵等於3的模域，則射影平面上有13個點和13條線，每條線上有4個點，經過每點有4條線。如果要通過公理系統來建立這個空間，就要在關聯公理中規定：每條線上不能有多於4個點。
簡史
畫法幾何的創始人G.蒙日在17世紀初期，J.克卜勒最早引進了無窮遠點概念(1604)。稍後，G.德扎格引進了無窮遠點，除證明了上面提到的他的著名定理(1639)外，還引進了交比，調和比，以及對於二次曲線的極點和極線等概念，證明了交比經過透視不變。在他的影響下，B.帕斯卡也研究了有關射影幾何的問題，並發表了他的著名定理（1640）。這些定理的特點是概括性強，只涉及關聯性質而不涉及度量性質（長度、角度、面積）。但他們在證明中卻用到了長度概念，而不是用嚴格的射影方法，他們也沒有意識到，自己的研究方向會導致產生一個新的幾何體系射影幾何。他們所用的是綜合法，隨著解析幾何和微積分的創立，綜合法讓位於解析法，射影幾何的探討也中斷了。
射影幾何的主要奠基人是 19世紀的J.-V.彭賽列。他是畫法幾何的創始人G.蒙日的學生。蒙日帶動了他的許多學生（C.－J.布里昂雄是其中之一）用綜合法研究幾何。由於德扎格和帕斯卡等的工作被長期忽視了，前人的許多工作他們不了解，不得不重新再做。1822年，彭賽列發表了射影幾何的第一部系統著作。他是認識到射影幾何是一個新的數學分支的第一個數學家。他通過幾何方法引進無窮遠虛圓點，研究了配極對應並用它來確立對偶原理。稍後，J.施泰納研究了利用簡單圖形產生較複雜圖形（例如二次曲線和二次曲面）的方法，線素二次曲線概念也是他引進的(1832)。為了擺脫坐標系對度量概念的依賴，K.G.C.von施陶特通過幾何作圖來建立直線上的點坐標系(1847)，進而使交比也不依賴於長度概念。由於忽視了連續公理的必要性，他建立坐標系的做法還不完善，但卻邁出了決定性的一步。
另一方面，運用解析法來研究射影幾何也有長足進展。首先是A.F.麥比烏斯創建一種齊次坐標系，把變換分為全等，相似，仿射，直射等類型，給出線束中四條線交比的度量公式等(1827)。接著，J.普呂克引進了另一種齊次坐標系，得到了平面上無窮遠線的方程，無窮遠圓點的坐標。他還引進了線坐標概念，於是從代數觀點就自然得到了對偶原理，並得到了關於一般線素曲線的一些概念。
在19世紀前半葉的幾何研究中，綜合法和解析法的爭論異常激烈；有些數學家完全否定綜合法，認為它沒有前途，而一些幾何學家，如M.沙勒，E.施圖迪和施泰納等，則堅持用綜合法而排斥解析法。還有一些人，如彭賽列，雖然承認綜合法有其局限性，在研究過程中也難免藉助於代數，但在著作中總是用綜合法來論證。他們的努力使綜合射影幾何形成一個優美的體系，而且用綜合法也確實形象鮮明，有些問題論證直接而簡潔。1882年，M.帕施建成第一個嚴格的射影幾何演繹體系。
把各種幾何和變換群相聯繫的是F.克萊因，他在埃爾朗根綱領(1872)中提出了這個觀點，並把幾種經典幾何看作射影幾何的子幾何，使這些幾何之間的關係變得十分明朗。這個綱領產生了巨大影響。但有些幾何，如黎曼幾何，不能納入這個分類法。後來é嘉當等在拓廣幾何分類的方法中作出了新的貢獻。
分支學科
算術、初等代數、高等代數、數論、歐式幾何、非歐幾何、解析幾何、微分幾何、代數幾何學、拓撲學、分形幾何、微積分學、實變函式論、機率和數理統計、複變函數論、泛函分析、偏微分方程、常微分方程、數理邏輯、模糊數學、運籌學、計算數學、突變理論、數學物理學。
