計算複雜性
正文
從可計算性到計算複雜性 什麼樣的問題類是可計算的？這是數學、數理邏輯學和早期計算機科學所關心的一個重要問題。為了回答這個問題，可以給出一個計算的模型，然後規定，凡是這個模型能計算的問題類就叫作可計算的，否則就叫作不可計算的。於是產生了各種計算的模型：圖靈機、遞歸函式、λ 演算、馬爾可夫算法和遞歸算法等。但是，會不會有一類問題，在一個模型中是可計算的，而在另一個模型中卻是不可計算的呢？如果這樣,一個問題類的可計算性就依賴於模型,而不是問題類本身的性質了。著名的丘奇－圖靈論題回答了這個問題。這個論題說：“凡是合理的計算模型都是等價的，即一個模型能算的問題類別的模型也能算，一個模型不能算的別的模型也不能算。”這個論題不是一個嚴格的命題，無法給於一般的證明，但可以對一個個具體的模型去驗證它的正確性。但是，對於一個問題類，只知道它能否計算還很不夠，更有實際意義的是要知道計算起來要耗費多少時間，要用多大的空間來存儲計算的中間結果等等。為了回答這些進一步的問題，就產生了計算複雜性理論。資源計算時間、存儲大小都稱為資源。嚴格地講，每一種資源的定義都依賴於特定的計算模型。對各種計算模型，資源的定義雖不一樣，但主要的可分為三類：
① 串列時間（簡稱時間） 它是計算過程中的總運算量，即把計算分成一些原始的步驟，完成這些步驟所需要的總時間。
② 空間 它是為了保存中間結果所需要的存儲器的大小。例如在計算時用一塊黑板來打草稿，每一單位面積假定可以寫一個符號，不用了還可以擦掉。在計算時所需黑板面積就是空間。
③ 並行時間 它是並行計算所需要的時間,亦即如果多人或多處理機協同計算，解決一個問題所需要的時間。
問題的大小和複雜性的度量 和可計算性一樣，複雜性總是對於一個特定的問題類來討論的，它包括無窮多個個別問題，有大有小。例如，對矩陣乘法這樣一個問題類,相對地說,100階矩陣相乘是個大問題,而二階矩陣相乘就是個小問題。可以把矩陣的階 n作為衡量問題大小的尺度。又如在圖論問題中,可以把圖的頂點數n作為衡量問題大小的尺度。一個個別問題在計算之前，總要用某種方式加以編碼,並可把這個編碼的長度 n作為衡量問題大小的尺度。
當給定一個算法以後,計算大小為n的問題所需要的時間、空間等就可以表示為 n的函式。這個函式就可作為該算法的時間或空間複雜性的度量。嚴格地講，是這個特定的問題類在某一特定計算模型中某一特定算法的複雜性之度量。當要解決的問題越來越大時，時間、空間等資源耗費將以什麼樣的速率增長,即當n趨向於無窮大時，這個函式的性狀如何，增長的階是什麼，這就是計算複雜性理論所要研究的主要問題。
上界和下界 在計算同一個問題類時，算法有好壞之別。例如,要確定一個具有n個頂點的無向圖中有沒有迴路，以前最好的算法所需工作空間為 S(n)=O(log2n)(S(n)=O(ƒ(n))的意思是當n充分大時,S(n)不超過ƒ(n)的一個正的常數倍)。但是最新的算法只需要O(logn)的工作空間就夠了。這說明，O(log2n)只是原來那個算法的複雜性，而並非這個迴路問題的內在複雜性。或者說O(log2n)是迴路問題空間複雜性的一個上界,而O(logn)則是一個更好的上界。對於迴路問題來說，還可以證明，任何算法都至少需要正比於logn的工作空間。也即對於任何算法, 空間複雜性S(n)=Ω(logn)(S(n)=Ω(ƒ(n))的意思是當n充分大時S(n)不小於ƒ(n)的一個正的常數倍）。 因此可以認為Ω(logn)是迴路問題空間複雜性的一個下界。一個問題類的內在複雜性介於最小的上界和最大的下界之間。在這個例子中兩者重合了,因此可以說迴路問題的空間複雜性正比於logn,記為S(n)=嘷(logn)。
又如,兩個n位二進整數的乘法在一個適當的模型之下,總運算量(時間)為O(n2)，對算法略加改進可以達到O(n1.5),現在最好算法的時間只需O(n·logn·loglogn)。如果進一步採用存儲修改機器做模型，則時間可以進一步縮短到O(n)。可見一個問題的複雜性是依賴於所選擇的模型的。
相似性原理 如上所述，一個問題類的時間、空間等資源的複雜性是依賴於模型的:在有的模型中較高,在另一些模型中則較低。現在較為重要而有特色的計算模型有：多帶圖靈機器、多變址隨機存取機器、存儲修改機器、齊一線路、向量機器、硬體修改機器等等。這樣一來，複雜性的問題仍然沒有一個統一的客觀依據。相似性原理解答了這個問題。按此原理，一個問題類內在的並行時間、空間和串列時間的複雜性在所有理想的計算模型中都沒有本質的差異。用數學的說法，各種模型可以互相模擬，而且模擬者需用的並行時間、空間和串列時間都分別不超過被模擬者所需的並行時間、空間和串列時間的一個多項式，三者同時成立。所以在只差一個多項式的範圍內，複雜性的確是一個不依賴於模型的客觀實在。這是丘奇－圖靈論題在複雜性理論中的新發展。對於上面提到的計算模型，相似性原理已被證明是正確的。
巡迴和周相 在上面提到的模型中，有的是串列模型，有的則是並行模型。如前所述，並行模型的串列時間相當於計算過程中的總運算量。至於串列模型的並行時間，可以認為它是一個叫作巡迴的量。簡而言之，巡迴是計算過程中周相的總數。而周相則是計算過程中的一個階段，在此階段內寫入工作空間的信息不會在同一階段中讀出。由此可見，串列模型的巡迴相應於並行模型的並行時間。對於一個問題類而言，存在一個高速並行算法的充要條件是可以找到一個具有小的巡迴數的串列算法。
對偶性原理 並行時間和空間之間還呈現出某種對稱的性質，這就是對偶性原理。例如可以證明，對於一個問題類而言，存在一個節省並行時間的算法的充要條件是存在一個節省工作空間的算法。因此在這個意義下並行時間和空間是可以互相轉換的。
平均複雜性和最壞情況複雜性 對於大小都為 n的不同問題，一個算法所需用的時間、空間等資源也可能不相同。那么如何定義它的複雜性？一種方法是考慮最不利的情況,例如，把大小為n的各問題中花費的最長時間作為時間的複雜性。另一種方法是對所有可能情況按某種分布取平均值，這就是平均複雜性。顯然，它不高於最壞情況複雜性。由於平均複雜性依賴於問題的分布，難於作數學的處理，所以常用的是最壞情況複雜性。
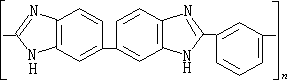
代數複雜性 相似性原理所涉及的模型主要研究計算中按位運算的總量時間，按位計的中間結果存儲量空間和計算的深度(並行時間)等等，所以可稱為按位的複雜性。代數的複雜性理論則研究在一個代數系統中（例如實數域中）從給定變數出發去計算某些函式所需要的代數運算（例如加法、乘法）代數判斷（例如大於或等於）的次數(時間),所需中間變元的個數(空間),計算的深度(並行時間)等等。在實際運算中，既不能給出一個無限長的實數，也不能在一個單位時間內完成兩個實數的乘法。真正的算術運算都是通過近似小數的按位運算得出來的。所以按位的複雜性具有更為基本的意義。通過下面的例子，可以得到關於代數複雜性的一些感性認識。通常兩個n階矩陣相乘要做n3次數乘法,V.斯特拉森找到了一個算法,只需做
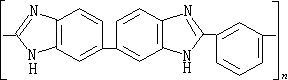次數乘法。此後這個上界又被許多人不斷改進到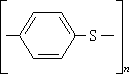
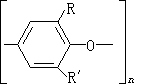,至1981年12月，又改進為
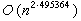。D.科普爾史密斯和S.維諾格拉特還證明：最好的算法不存在，也就是說這個上界可以永遠改進下去。 參考書目
A.V.Aho,J.E.Hopcroft and J.D.Ullman,The Design and Analysis of Computer Algorithms,Addison-Wesley, Reading Mass., 1974.
洪加威著:《計算──理論和現實的可計算性》,科學出版社，北京，1984。
J.E.Hopcroft and J.D.Ullman,Introduction to AutoMata Theory, languages and Computation,Addison-Wesley,Reading Mass., 1979.
