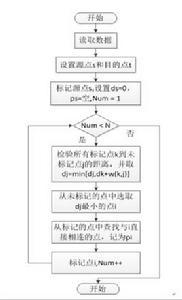
定義
Dijkstra算法一般的表述通常有兩種方式，一種用永久和臨時標號方式，一種是用OPEN, CLOSE表的方式，這裡均採用永久和臨時標號的方式。注意該算法要求圖中不存在負權邊。
原理
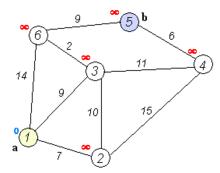Dijkstra算法運行動畫過程
迪傑斯特拉算法
迪傑斯特拉算法 迪傑斯特拉算法
迪傑斯特拉算法1.首先，引入一個輔助向量D，它的每個分量 D 表示當前所找到的從起始點 （即源點 ）到其它每個頂點 的長度。
例如，D[3] = 2表示從起始點到頂點3的路徑相對最小長度為2。這裡強調相對就是說在算法執行過程中D的值是在不斷逼近最終結果但在過程中不一定就等於長度。
迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法2.D的初始狀態為：若從 到 有弧（即從 到 存在連線邊），則D 為弧上的權值（即為從 到 的邊的權值）；否則置D 為∞。
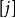迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法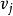
迪傑斯特拉算法
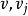迪傑斯特拉算法顯然，長度為 D = Min{ D | ∈V } 的路徑就是從 出發到頂點 的長度最短的一條路徑，此路徑為( )。
迪傑斯特拉算法 迪傑斯特拉算法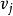 迪傑斯特拉算法3.那么，下一條長度次短的是哪一條呢？也就是找到從源點 到下一個頂點的最短路徑長度所對應的頂點，且這條最短路徑長度僅次於從源點 到頂點 的最短路徑長度。
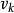迪傑斯特拉算法
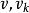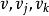迪傑斯特拉算法
迪傑斯特拉算法 迪傑斯特拉算法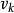 迪傑斯特拉算法 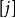迪傑斯特拉算法 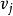迪傑斯特拉算法 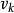迪傑斯特拉算法假設該次短路徑的終點是 ，則可想而知，這條路徑要么是( )，或者是( )。它的長度或者是從 到 的弧上的權值，或者是D 加上從 到 的弧上的權值。
迪傑斯特拉算法
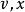迪傑斯特拉算法
迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法4.一般情況下，假設S為已求得的從源點 出發的最短路徑長度的頂點的集合，則可證明：下一條次最短路徑（設其終點為 ）要么是弧( )，或者是從源點 出發的中間只經過S中的頂點而最後到達頂點 的路徑。
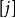迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法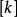
迪傑斯特拉算法
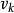迪傑斯特拉算法 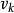迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法因此，下一條長度次短的的最短路徑長度必是D = Min{ D | ∈V-S }，其中D 要么是弧( )上的權值，或者是D ( ∈S)和弧( , )上的權值之和。
算法描述如下：
迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法 迪傑斯特拉算法1）令arcs表示弧上的權值。若弧不存在，則置arcs為∞（在本程式中為MAXCOST）。S為已找到的從 出發的的終點的集合，初始狀態為空集。那么，從 出發到圖上其餘各頂點 可能達到的長度的初值為D=arcs[Locate Vex(G, )]， ∈V；
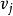迪傑斯特拉算法 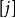迪傑斯特拉算法 迪傑斯特拉算法2）選擇 ，使得D =Min{ D | ∈V-S } ；
迪傑斯特拉算法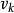 迪傑斯特拉算法3）修改從 出發的到集合V-S中任一頂點 的最短路徑長度。
問題描述
在無向圖 G=(V,E) 中，假設每條邊 E[i] 的長度為 w[i]，找到由頂點 V0 到其餘各點的最短值。
算法思想
按路徑長度遞增次序產生算法：
把頂點集合V分成兩組：
（1）S：已求出的頂點的集合（初始時只含有源點V0）
（2）V-S=T：尚未確定的頂點集合
將T中頂點按遞增的次序加入到S中，保證：
（1）從源點V0到S中其他各頂點的長度都不大於從V0到T中任何頂點的最短路徑長度
（2）每個頂點對應一個距離值
S中頂點：從V0到此頂點的長度
T中頂點：從V0到此頂點的只包括S中頂點作中間頂點的最短路徑長度
依據：可以證明V0到T中頂點Vk的，或是從V0到Vk的直接路徑的權值；或是從V0經S中頂點到Vk的路徑權值之和
（反證法可證）
求最短路徑步驟
算法步驟如下：
G={V,E}
1. 初始時令 S={V0},T=V-S={其餘頂點}，T中頂點對應的距離值
若存在<V0,Vi>，d(V0,Vi)為<V0,Vi>弧上的權值
若不存在<V0,Vi>，d(V0,Vi)為∞
2. 從T中選取一個與S中頂點有關聯邊且權值最小的頂點W，加入到S中
3. 對其餘T中頂點的距離值進行修改：若加進W作中間頂點，從V0到Vi的距離值縮短，則修改此距離值
重複上述步驟2、3，直到S中包含所有頂點，即W=Vi為止
算法實現
pascal語言
下面是該算法的Pascal程式
主程式調用：求長度：初始化t，然後dijkstra(qi,t,c,d)
求路徑：make(m,d,e) ，m是終點
C語言
下面是該算法的C語言實現
大學經典教材<<數據結構>>(C語言版 嚴蔚敏 吳為民 編著) 中該算法的實現
堆最佳化
思考
該算法複雜度為n^2,我們可以發現，如果邊數遠小於n^2,對此可以考慮用堆這種數據結構進行最佳化，取出最短路徑的複雜度降為O(1)；每次調整的複雜度降為O（elogn）；e為該點的邊數，所以複雜度降為 O(( m+ n)log n)。
實現
1. 將源點加入堆，並調整堆。
2. 選出堆頂元素u（即代價最小的元素），從堆中刪除，並對堆進行調整。
3. 處理與u相鄰的，未被訪問過的，滿足三角不等式的頂點
1):若該點在堆里，更新距離，並調整該元素在堆中的位置。
2):若該點不在堆里，加入堆，更新堆。
4. 若取到的u為終點，結束算法；否則重複步驟2、3。
