隨機化算法，是一種基於隨機方法，依賴於機率大小的一種算法。這種算法看上去是憑著運氣做事，其實，隨機化算法是有一定的理論基礎的，我們可以想像，在[1,10000]這個閉區間裡，隨機1000次，隨機到2這個數的幾率是多大，何況1000次的隨機在計算機程式中僅僅是一眨眼的功夫。可以看出，隨機化算法有著廣闊的前景。只是由於隨機化算法比較難於掌控，所以並不是很多人都接觸過他，但肯定有很多人都聽說過。
隨機數
隨機數在隨機化算法設計中扮演著十分重要的角色。在現實計算機上無法產生真正的隨機數，因此在隨機化算法中使用的隨機數都是一定程度上隨機的，即偽隨機數。
線性同餘法是產生偽隨機數的最常用的方法。由線性同餘法產生的隨機序列a0,a1,…,an滿足：
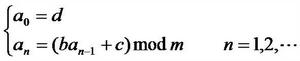隨機化算法其中b≥0，c≥0，d≤m。d稱為該隨機序列的種子。如何選取該方法中的常數b、c和m直接關係到所產生的隨機序列的隨機性能。這是隨機性理論研究的內容。從直觀上看，m應取得充分大，因此可取m為機器大數，另外應取gcd(m,b)=1，因此可取b為一素數。
數值隨機化算法
1.用隨機投點法計算π值
設有一半徑為r的圓及其外切四邊形。向該正方形隨機地投擲n個點。設落入圓內的點數為k。由於所投入的點在正方形上均勻分布，因而所投入的點落入圓內的機率為
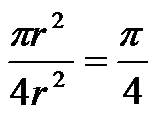隨機化算法
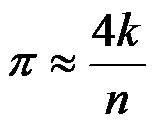隨機化算法| double Darts(int n) { // 用隨機投點法計算值 static RandomNumber dart; int k=0; for (int i=1;i <=n;i++) { double x=dart.fRandom(); double y=dart.fRandom(); if ((x*x+y*y)<=1) k++; } return 4*k/double(n); } |  |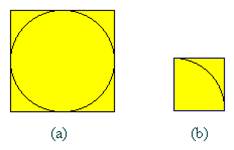
2.計算定積分
設f(x)是[0，1]上的連續函式，且0≤f(x)≤1。需要計算的積分為
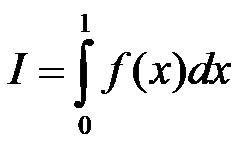隨機化算法
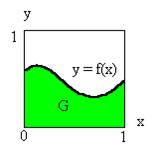
隨機化算法在圖所示單位正方形內均勻地作投點試驗，則隨機點落在曲線下面的機率為：
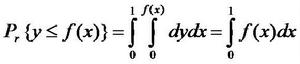隨機化算法假設向單位正方形內隨機地投入n個點(xi,yi)。如果有m個點落入
G內，則隨機點落入G內的機率
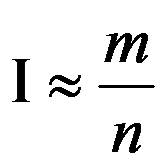隨機化算法3.解非線性方程組
求解下面的非線性方程組
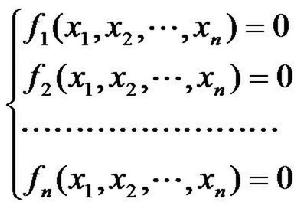隨機化算法其中，x1,x2,…,xn是實變數，fi是未知量x1,x2,…,xn的非線性實函式。要求確定上述方程組在指定求根範圍內的一組解
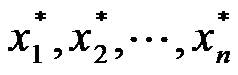隨機化算法在指定求根區域D內，選定一個隨機點x0作為隨機搜尋的出發點。在算法的搜尋過程中，假設第j步隨機搜尋得到的隨機搜尋點為xj。在第j+1步，計算出下一步的隨機搜尋增量Δxj。從當前點xj依Δxj得到第j+1步的隨機搜尋點。當x<ε時，取為所求非線性方程組的近似解。否則進行下一步新的隨機搜尋過程。
經典計算機算法介紹
| 算法是計算機科學中一門古老而常新的學科，就像一個人的思維能力一樣，其重要性對於計算機性能的分析、套用與改進有著至不言而喻的地位。而隨著計算機科學技術的發展，新的算法也隨著新的套用漸漸出現，但總有一些算法由於其本身具有的特點以及對計算機科學發展做出的卓越貢獻而成為經典，本任務就是要介紹這些經典算法。 |
