約束最佳化方法
正文
尋求具有約束條件的線性或非線性規劃問題解的數值算法。假設ƒ(尣),gi(尣)(i=1,2,…,m)是n維歐幾里得空間Rn中的實值函式。所謂約束最佳化問題,是指在約束條件gi(尣)≤0(i=1,2,…,m)之下求一點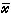
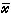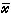,使ƒ(尣)≥ƒ()，點稱為最優解。約束最佳化問題當ƒ(尣)、gi(尣)(i=1,2,…,m)均為凸函式時稱為凸規劃。凸函式有很多已知特性，因此凸規划算法的研究進展較快。線性規劃是凸規劃的最簡單的情形，可以用單純形方法等求解。約束最佳化問題當ƒ(尣)是二次函式而gi(尣)(i=1,2,…,m)是線性函式時稱為二次規劃。G.B.丹齊克和P.沃爾夫於1963年將單純形方法作了修改，用以求解凸二次規劃，得到只經過有限次疊代即可達到最優解的算法。 對於只有等式約束的非線性規劃，經典的拉格朗日乘子法指出，在對函式加以一定限制下，最優解可在一組函式方程的解集中去尋求，但是並未指出行之有效的算法。1951年，H.W.庫恩和A.W.塔克爾發表“論非線性規劃”一文後，隨著計算技術的迅速發展，線性約束的非線性規劃出現了不少行之有效的算法。在非線性約束規劃的研究上，近十幾年來也有相當的進展。
可行方向法 根據逐次沿可行方向求可行解點的疊代思想構造一點列{尣k}，使其滿足某種給定要求的算法稱為可行方向法。假設已知可行解為尣(k),若能找到一個向量
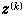與步長數λk>0,使
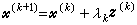,而當0≤λ≤λk時，線段尣(k)+λ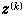屬於約束集，則 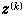稱為約束集在尣(k)處的一個可行方向。可行方向法的關鍵在於適當選取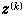, 點列{尣(k)}符合一般疊代法的要求。對線性約束的情形，當ƒ(尣)為可微凸函式時有三種較為有效的求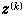的算法:G.藻滕代克於1960年提出的可行方向法, 取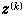＝y(k)- 尣(k)，其中y(k)為ƒ(尣)在 尣(k)處的線性近似函式
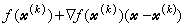線上性約束下達到最小值的最優解。J.B.羅森於1960年提出的梯度投影法,運用在尣(k)處投影矩陣pk的公式,取最速下降方向－墷ƒ(尣(k))在 尣(k)所處的約束邊界面上的投影方向－pk墷ƒ(尣(k))為
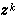,從而避免了每疊代一次就要解一個線性規劃的手續。P.沃爾夫於1963年提出的既約梯度法，他套用消去基變數的方法和ƒ(尣)的既約梯度的概念,構造出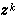。 這三種方法所產生的點列{尣(k)}雖然可以使函式值序列{ƒ(尣(k)}單調下降,但是它卻不一定收斂於最優解。因此,後來陸續有不少研究工作,對原有方法進行種種修正,如採取攝動和轉軸變換等技巧，而得出具有收斂性的各種新方法。1969年D.戈德福布結合梯度投影法與變尺度法提出了一種可行方向法，對二次凸規劃是有限步收斂的。這些方法都可以推廣用於處理非線性約束的情形。但是，算法程式都比較複雜。J.阿巴迪和J.卡彭特爾於1969年將既約梯度法加以推廣,提出了廣義既約梯度法(GRG法)用來求解具有非線性約束的最最佳化問題。實際計算的效果說明，廣義既約梯度法是一種很好的算法。 上述線性近似型算法的收斂速度，一般都不高於超線性的。對二階可微的函式ƒ(尣)，在尣(k)處若用二次函式
·
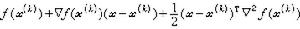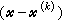來近似，進而對可微函式ƒ(尣)又用種種變尺度矩陣Hk去代替近似式中的矩陣墷2ƒ（尣(k)）,將約束問題的求解化為求一系列二次規劃的解，這類方法統稱為序貫二次規劃法，1963年R.B.威爾森對二階可微函式ƒ(尣)，gi(尣)(i=1,2,…,m)提出將拉格朗日函式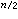
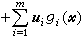在已知點（尣(k)，u(k)）處用二次近似函式來逼近，而對約束仍用線性近似函式逼近，並證明了在最優解附近，點列{尣(k)}是二階收斂的。若用二次函式
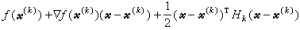在尣(k)處逼近目標函式ƒ(尣),其中Hk是正定函式,同時象無約束最最佳化方法中的變尺度算法一樣，利用計算過程中得到的信息和變尺度公式來更新Hk，這種逐次二次規划算法也稱為約束變尺度算法。它是求解帶非線性約束的最最佳化問題的重要方法之一。 序貫無約束極小化法 1943年R.庫朗對於僅帶一個約束等式g(尣)=0的問題,引入參數t>0，研究函式ƒ(尣)＋t【g(尣)】2的平穩點尣(t)在t→∞時與原問題的關係。對於具有不等式約束gi(尣)≤0(i=1,2,…,m)的非線性規劃問題，則作函式
；
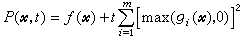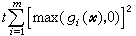為當尣違反“規定”時的罰款項，於是p(尣,t)就是應支付的總代價。因此,p(尣,t)被稱為罰函式，而t稱為罰因子。在適當的假設下,p(尣,t)在對尣不加約束的情形下的最優解尣(t),當t→∞時趨於原問題的最優解。這種方法稱為罰函式法。由此就可以用逐漸加大tk的方法來求得原問題近似解尣(tk)。為了克服p(尣,t)的黑塞矩陣在t→∞時容易產生病態的缺點,W.I.贊格威爾於1967年提出精確罰函式E(尣,t)，證明了在適當的假設下,存在t0>0,當t≥t0時E(尣,t)的無約束最優解尣(t)就是原問題的最優解。於是把有約束的最最佳化問題化為一個無約束的最最佳化問題。但是這種精確罰函式不是可微的，因而不便於利用一般無約束最佳化方法。M.R.赫斯泰尼斯和M.J.D.鮑威爾結合拉格朗日乘子法和罰函式法的特點，於1969年對約束為等式的情形提出可微的增廣拉格朗日函式
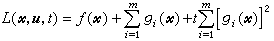,並指出在適當的假設下,存在t0>0,對任意取定的t≥t0，在最優乘子
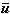處，L(尣,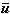,t)的無約束最優解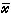必為原問題的最優解，還給出了逐步調整u和t的辦法。以後陸續有不少工作對一般可微非線性規劃，構造了各種不同的可微增廣拉格朗日函式,並給出了算法的疊代程式。這類方法統稱為廣義乘子法。K.R.弗里希鑒於罰函式法產生的點列 {尣(tk)}是從約束集的外部來逼近在約束邊界上的最優解,於1955年提出所謂障礙函式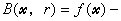
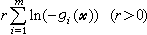,可使B(尣,r)的無約束最優解尣(r)在約束集內達到,而當r→0時,尣(r)趨於原問題的最優解。1961年,C.W.卡羅爾提出了另一種典型的障礙函式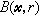
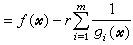。當r→0時,B(尣,r)的黑塞矩陣也可能出現病態現象。 對兼有等式和不等式約束的最最佳化問題，可結合使用罰函式與障礙函式而構造出混合型函式來求解；對兼有線性和非線性約束的最最佳化問題，可僅將非線性約束納入p(尣,t)（或B(尣,r),或L(尣,u,t)），將問題化為線上性約束下p(尣,t)（或B(尣,r),或L(尣，u，t)）的極小化問題。
對於不可微的凸規劃，近十多年來有人用次梯度或差分等概念來建立算法。設ƒ為Rn中的凸函式,若矢量
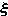滿足
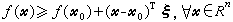,則矢量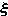稱為函式ƒ 在點尣0處的一個次梯度。不可微凸規劃的最優解在一定條件下滿足以次梯度表示的推廣的庫恩－塔克爾條件(見非線性規劃)。函式在一點的次梯度不一定是惟一的。可微函式在一點的梯度若不為零,其負梯度方向必是函式在此點的一個下降方向。然而不可微函式在一點的某些負次梯度可以不是函式的下降方向。這將導致上述可微情況的約束最佳化算法對於不可微凸規劃往往會失敗。不可微凸規劃的次梯度算法類的基本疊代公式是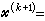
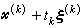，這裡tk和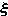(k)分別是按一定規則選定的步長和點 尣(k)的次梯度(或近似次梯度)。在一些適當的條件下可證明,次梯度算法產生的點列{尣(k)}收斂到問題的最優解。 贊格威爾1969年提出用統一的觀點研究算法。他的基本思想是，將算法看成是一個點到集的映像。在一些假設下由上半連續的點到集映像產生的點列 {尣(k)}收斂於最優解。從而統一了不少已有算法的收斂性的研究。這方面的工作還在不斷發展。
參考書目
M.阿弗里爾著,李元熹等譯:《非線性規劃-分析與方法》,上冊,上海科學技術出版社,上海,1979。(M.Avriel,Nonlinear Programming-Analysis and Method,Prentice-hall,Englewood Cliffs,New Jersey,1976.)
A.V.Fiacco and G.P.McCormick,Nonlinear Pro-gramming Sequential unconstrained Minimization Techiques, John Wiley & Sons, New York, 1968.
