通項公式
a(n)=a(1)+(n-1)×d, 等差數列求和公式
等差數列求和公式前n項和公式
S(n)=n*a(1)+n*(n-1)*d/2或S(n)=n*(a(1)+a(n))/2
注意:n是正整數(相當於n個等差中項之和)
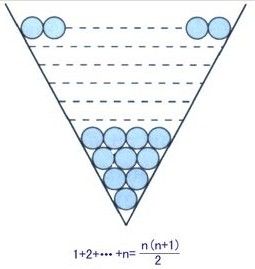
等差數列前N項求和,實際就是梯形公式的妙用:
上底為:a1首項,下底為a1+(n-1)d,高為n.
即[a1+a1+(n-1)d]*n/2=a1n+n(n-1)d/2.
推論
一.從通項公式可以看出,a(n)是n的一次函式(d≠0)或常數函式(d=0),(n,an)排在一條直線上,由前n項和公式知,S(n)是n的二次函式(d≠0)或一次函式(d=0,a1≠0),且常數項為0。
二.從等差數列的定義、通項公式,前n項和公式還可推出:
a(1)+a(n)=a(2)+a(n-1)=a(3)+a(n-2)=…=a(k)+a(n-k+1),(類似:p(1)+p(n)=p(2)+p(n-1)=p(3)+p(n-2)=...=p(k)+p(n-k+1)),k∈{1,2,…,n}
三.若m,n,p,q∈N*,且m+n=p+q,則有a(m)+a(n)=a(p)+a(q),S(2n-1)=(2n-1)*a(n),S(2n+1)=(2n+1)*a(n+1),S(k),S(2k)-S(k),S(3k)-S(2k),…,S(n)*k-S(n-1)*k…或等差數列,等等。
若m+n=2p,則a(m)+a(n)=2*a(p)
(對3的證明:p(m)+p(n)=b(0)+b(1)*m+b(0)+b(1)*n=2*b(0)+b(1)*(m+n)p(p)+p(q)=b(0)+b(1)*p+b(0)+b(1)*q=2*b(0)+b(1)*(p+q);因為m+n=p+q,所以p(m)+p(n)=p(p)+p(q))
四.其他推論
①和=(首項+末項)×項數÷2(證明:s(n)=[n,n^2]*[1,1/2;0,1/2]*[b(0);b(1)]=n*b0+1/2*b1*n+1/2*b1*n^2(p(1)+p(n))*n/2=(b(0)+b(1)+b(0)+b(1)*n)*n/2=n*b0+1/2*b1*n+1/2*b1*n^2=s(n))證明原理見高斯算法項數=(末項-首項)÷公差+1(證明:(p(n)-p(1))/b(1)+1=(b(0)+b(1)*n-(b(0)+b(1)))/b(1)+1=(b(1)*(n-1))/b(1)+1=n-1+1=n)
②首項=2和÷項數-末項或末項-公差×(項數-1)
③末項=2和÷項數-首項(以上2項為第一個推論的轉換)
④末項=首項+(項數-1)×公差(上一項為第二個推論的轉換)
推論3證明若m,n,p,q∈N*,且m+n=p+q,則有a(m)+a(n)=a(p)+a(q)
如a(m)+a(n)=a(1)+(m-1)*d+a(1)+(n-1)*d=2*a(1)+(m+n-2)*d
同理得,a(p)+a(q)=2*a(1)+(p+q-2)*d
又因為m+n=p+q;a(1),d均為常數
所以若m,n,p,q∈N*,且m+n=p+q,則有a(m)+a(n)=a(p)+a(q)
若m,n,p∈N*,且m+n=2p,則有a(m)+a(n)=2a(p)
註:1.常數列不一定成立2.m,p,q,n屬於自然數數列為偶數項,求首尾項相加,用它的和除以2
等差中項
等差中項即等差數列頭尾兩項的和的一半.但求等差中項不一定要知道頭尾兩項.
等差數列中,等差中項一般設為A(r).當A(m),A(r),A(n)成等差數列時。
A(m)+A(n)=2*A(r),所以A(r)為A(m),A(n)的等差中項,且為數列的平均數。並且可以推知n+m=2*r。
且任意兩項a(m),a(n)的關係為:a(n)=a(m)+(n-m)*d,(類似p(n)=p(m)+(n-m)*b(1),相當容易證明它可以看作等差數列廣義的通項公式。
等差數列的套用日常生活中,人們常常用到等差數列如:在給各種產品的尺寸劃分級別時,當其中的最大尺寸與最小尺寸相差不大時,常按等差數列進行分級。
若為等差數列,且有a(n)=m,a(m)=n.則a(m+n)=0。
其實,中國古代南北朝的張丘建早已在《張丘建算經》提到等差數列了:今有女子不善織布,逐日所織的布以同數遞減,初日織五尺,末一日織一尺,計織三十日,問共織幾何?
書中的解法是:並初、末日織布數,半之,余以乘織訖日數,即得。
這相當於給出了S(n)=(a(1)+a(n))/2*n的求和公式