一般定義
等差數列求和公式等差數列遵守的形式,
可規定b為數列的0項,記為a0,k為數列的公差,記為d,y為通項公式,記為an
等差數列求和公式則
等差數列求和公式
等差數列求和公式對應的求和數列其中正整數
擴展:冪次數列
等差數列求和公式數列:
等差數列求和公式求和數列:
等差數列求和公式方陣
等差數列是冪次數列的特殊形式
等差數列求和公式數列:
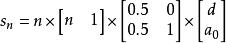等差數列求和公式求和數列:
其他結論
等差數列求和公式首項： /末項-(項數-1)×公差
等差數列求和公式末項：
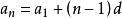等差數列求和公式通項公式：
等差數列求和公式項數：
等差數列求和公式公差：
等差數列求和公式
等差數列求和公式
等差數列求和公式如：數列1,3,5,7,……,97,99 公差就是d=3-1=2 將 推廣到 ，則為：
a1,a2,a3....an,n=奇數，Sn=（a（（n-1）/2)）*((n-1）/2)
特殊性質
等差數列求和公式
等差數列求和公式1.在數列 中,若 ,則有:
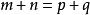等差數列求和公式①若 ,則am+an=ap+aq.
②若m+n=2q,則am+an=2aq.
2.在等差數列中，若Sn為該數列的前n項和，S2n為該數列的前2n項和，S3n為該數列的前3n項和，則Sn，S2n-Sn，S3n-S2n也為等差數列。
求和公式（字母）
等差數列求和公式 等差數列求和公式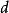
等差數列求和公式
等差數列求和公式 等差數列求和公式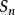
等差數列求和公式設首項為 , 末項為 , 項數為 , 公差為 , 前 項和為 , 則有:
等差數列求和公式① ;
等差數列求和公式② ;
等差數列求和公式③ ;
等差數列求和公式
等差數列求和公式④ , 其中 ..
等差數列求和公式當d≠0時，Sn是n的二次函式，（n，Sn）是二次函式 的圖象上一群孤立的點。利用其幾何意義可求前n項和Sn的最值。
注意：公式一二三事實上是等價的，在公式一中不必要求公差等於一。
求和推導
證明：由題意得：
Sn=a1+a2+a3+。。。+an①
Sn=an+a（n-1）+a（n-2）+。。。+a1②
①+②得：
2Sn=[a1+an]+[a2+a(n-1)]+[a3+a(n-2)]+...+[a1+an](當n為偶數時)
Sn={[a1+an]+[a2+a(n-1)]+[a3+a(n-2)]+...+[a1+an]}/2
Sn=n（A1+An）/2 (a1，an，可以用a1+（n-1）d這種形式表示可以發現括弧裡面的數都是一個定值，即A1+An）
求和公式（文字）
【（首項+末項）×項數】÷2
首項×項數+【項數（項數-1）×公差】/2
{【2首項+（項數-1）×公差】項數}/2
