指數的定義
指數是冪運算aⁿ(a≠0)中的一個參數,a為底數,n為指數,指數位於底數的右上角。
![指數[數學用語]](/img/1/18f/wZwpmLxQDN5kTO0YjM0IDN0UTMyITNykTO0EDMwAjMwUzL2IzL1UzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/4/2b3/wZwpmLwIjN1MzM1cTN1ATN0UTMyITNykTO0EDMwAjMwUzL3UzLxEzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]當指數 時,
![指數[數學用語]](/img/1/635/wZwpmLxYjN5AzMwITN2IDN0UTMyITNykTO0EDMwAjMwUzLyUzL3IzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/3/ccf/wZwpmL1YzMycjN1ADO3EDN0UTMyITNykTO0EDMwAjMwUzLwgzLyAzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]當指數 ,且n為整數時,
![指數[數學用語]](/img/5/8c5/wZwpmL3YDMyYTO4YTM0EDN0UTMyITNykTO0EDMwAjMwUzL2EzLzAzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/b/85b/wZwpmLyEDO5ADMwMzNxIDN0UTMyITNykTO0EDMwAjMwUzLzczLyQzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]當指數 時,
![指數[數學用語]](/img/2/7d9/wZwpmL0czMxUjM1cTN1ATN0UTMyITNykTO0EDMwAjMwUzL3UzL4AzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]當指數 時,稱為平方
![指數[數學用語]](/img/0/878/wZwpmL1UTOxQTN5gDM5IDN0UTMyITNykTO0EDMwAjMwUzL4AzL0AzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]當指數 時,稱為立方
冪運算的指數
冪運算(指數運算)是一種關於冪的數學運算。同底數冪相乘,底數不變,指數相加;同底數冪相除,底數不變,指數相減。冪的冪,底數不變,指數相乘。下面a≠0。
![指數[數學用語]](/img/b/c5f/wZwpmL4QTNzMzNzMjM0EDN0UTMyITNykTO0EDMwAjMwUzLzIzL2AzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]1)
![指數[數學用語]](/img/f/7fa/wZwpmL1gTO5QjM0UTM5IDN0UTMyITNykTO0EDMwAjMwUzL1EzL3UzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]2)
![指數[數學用語]](/img/2/95d/wZwpmL0MjM4gzM5ATO4EDN0UTMyITNykTO0EDMwAjMwUzLwkzL3AzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]3)
![指數[數學用語]](/img/1/543/wZwpmLwQjN4kDNwMzNxIDN0UTMyITNykTO0EDMwAjMwUzLzczL2czLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]4)
![指數[數學用語]](/img/a/6b8/wZwpmLzUDNxQTMwMzNxIDN0UTMyITNykTO0EDMwAjMwUzLzczL3EzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]5)
對數運算中的指數
![指數[數學用語]](/img/f/87d/wZwpmL2IjM4EzN5gDM5IDN0UTMyITNykTO0EDMwAjMwUzL4AzLwEzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/2/e11/wZwpmL2czNwATM4ADMwADN0UTMyITNykTO0EDMwAjMwUzLwAzLyMzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/a/e3f/wZwpmL1AzN1kDO3ATMwEDN0UTMyITNykTO0EDMwAjMwUzLwEzL4UzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/9/b7b/wZwpmLxUTM4kDNykzN5ADN0UTMyITNykTO0EDMwAjMwUzL5czL0YzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/5/5d5/wZwpmLyATN5ITMxMDO4EDN0UTMyITNykTO0EDMwAjMwUzLzgzL0YzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/7/d12/wZwpmL4ADN4MTOwMDO4EDN0UTMyITNykTO0EDMwAjMwUzLzgzLzYzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/a/e3f/wZwpmL1AzN1kDO3ATMwEDN0UTMyITNykTO0EDMwAjMwUzLwEzL4UzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/2/e11/wZwpmL2czNwATM4ADMwADN0UTMyITNykTO0EDMwAjMwUzLwAzLyMzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/9/b7b/wZwpmLxUTM4kDNykzN5ADN0UTMyITNykTO0EDMwAjMwUzL5czL0YzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]如果 ,即 的 次方等於 (且 ),那么數 叫做以 為底 的對數,記作
![指數[數學用語]](/img/2/a6a/wZwpmLyUzM3YDOwgTN2IDN0UTMyITNykTO0EDMwAjMwUzL4UzLyAzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/2/e11/wZwpmL2czNwATM4ADMwADN0UTMyITNykTO0EDMwAjMwUzLwAzLyMzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/9/b7b/wZwpmLxUTM4kDNykzN5ADN0UTMyITNykTO0EDMwAjMwUzL5czL0YzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/a/e3f/wZwpmL1AzN1kDO3ATMwEDN0UTMyITNykTO0EDMwAjMwUzLwEzL4UzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/2/e11/wZwpmL2czNwATM4ADMwADN0UTMyITNykTO0EDMwAjMwUzLwAzLyMzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/9/b7b/wZwpmLxUTM4kDNykzN5ADN0UTMyITNykTO0EDMwAjMwUzL5czL0YzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]其中, 叫做對數的底數, 叫做真數, 叫做“以 為底 的對數”。由此可見,在某種情況下(基數>0,且不為1),指數運算中的指數可以通過對數運算求解得到。
指數函式
![指數[數學用語]](/img/a/b40/wZwpmLwgTM2gzMxMDO4EDN0UTMyITNykTO0EDMwAjMwUzLzgzLygzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/5/5d5/wZwpmLyATN5ITMxMDO4EDN0UTMyITNykTO0EDMwAjMwUzLzgzL0YzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/7/d12/wZwpmL4ADN4MTOwMDO4EDN0UTMyITNykTO0EDMwAjMwUzLzgzLzYzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/f/08c/wZwpmLzETO0cTN5gDM5IDN0UTMyITNykTO0EDMwAjMwUzL4AzLygzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]一般地,形如(且)()的函式叫做指數函式(exponential function) ,也就是說以指數為自變數,底數為大於0且不等於1的常量的函式稱為指數函式,它是初等函式中的一種。
指數函式圖像如下圖所示
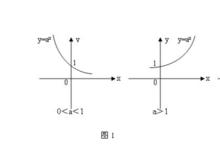 圖1 指數函式圖像
圖1 指數函式圖像指數的故事
曾經有人問愛因斯坦,世界上什麼事情最可怕?愛因斯坦說:“複利最可怕。”
![指數[數學用語]](/img/2/e11/wZwpmL2czNwATM4ADMwADN0UTMyITNykTO0EDMwAjMwUzLwAzLyMzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/1/036/wZwpmL3QzM5YjNzMjM0EDN0UTMyITNykTO0EDMwAjMwUzLzIzL3EzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/a/e3f/wZwpmL1AzN1kDO3ATMwEDN0UTMyITNykTO0EDMwAjMwUzLwEzL4UzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/9/237/wZwpmL1UTO5ATO0MjN1ATN0UTMyITNykTO0EDMwAjMwUzLzYzLxEzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/1/036/wZwpmL3QzM5YjNzMjM0EDN0UTMyITNykTO0EDMwAjMwUzLzIzL3EzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/a/e3f/wZwpmL1AzN1kDO3ATMwEDN0UTMyITNykTO0EDMwAjMwUzLwEzL4UzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/a/e3f/wZwpmL1AzN1kDO3ATMwEDN0UTMyITNykTO0EDMwAjMwUzLwEzL4UzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/4/b67/wZwpmL4MjM2QTO1ADO3EDN0UTMyITNykTO0EDMwAjMwUzLwgzLwgzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/3/cf4/wZwpmL4gTO0QTNwgTN2IDN0UTMyITNykTO0EDMwAjMwUzL4UzL0gzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]複利就是將本金按一定利息存入銀行,到期將利息計入本金繼續存入銀行,本利不斷增加。如果本金為 ,年利息率為 , 年後可以從銀行取出的錢為 。一般年利率 不會超過15%,而指數項,即存入銀行的年限 卻增長很快,當 足夠大時,本利相加會達到極其大的值。紐約曼哈頓地區是早期移民以價值200美元的珠寶從印地安人手中買下的,如果當初將200美元存入銀行,至今本息比現在曼哈頓的全部房產價值還要高。如果現在存入銀行1000元,年利率5%,若計複利的話,那么200年後的便可以從銀行取到 元,即 元。
![指數[數學用語]](/img/2/f4d/wZwpmLwQTO2EjN4kTNwMDN0UTMyITNykTO0EDMwAjMwUzL5UzLwYzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/6/495/wZwpmLycDOyATMxMzMzIDN0UTMyITNykTO0EDMwAjMwUzLzMzL1AzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/7/4a3/wZwpmL1EDNzMDN2cjN1IDN0UTMyITNykTO0EDMwAjMwUzL3YzL1czLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/a/e3f/wZwpmL1AzN1kDO3ATMwEDN0UTMyITNykTO0EDMwAjMwUzLwEzL4UzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/8/97b/wZwpmLxgTO3gDMyUjNxIDN0UTMyITNykTO0EDMwAjMwUzL1YzLygzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/d/048/wZwpmL1ADM1czM1IzM0IDN0UTMyITNykTO0EDMwAjMwUzLyMzL3YzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/2/480/wZwpmLxQDNzQDOwMjM4IDN0UTMyITNykTO0EDMwAjMwUzLzIzL1EzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/8/e2e/wZwpmL2IjM2UTNzMjM0EDN0UTMyITNykTO0EDMwAjMwUzLzIzL4IzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]傳說在古印度有位國王要賞賜一位宰相,就問宰相想要什麼,宰相拿出一張西洋棋的棋盤。笑著說,我只求您給我一些麥粒,在第一個格子裡放一粒( ),第二格子裡放兩粒( ),第三個格子裡放四粒( ),也就是第 個格子裡放 粒,直到每個格子的麥粒放好.國王以為這太簡單了,就爽快地答應了。可是等到真要執行這個諾言時國王卻不得不反悔了.這是為什麼呢?西洋棋棋盤共有64個格,按宰相的要求總共需要的麥粒數為等比數列 的和,即為 粒。若1公斤麥粒5萬粒,那么總共需要的麥粒為 噸。這些麥粒也許把全國的麥子全拿來都不夠,國王怎么可能答應呢?
![指數[數學用語]](/img/a/e3f/wZwpmL1AzN1kDO3ATMwEDN0UTMyITNykTO0EDMwAjMwUzLwEzL4UzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/a/e3f/wZwpmL1AzN1kDO3ATMwEDN0UTMyITNykTO0EDMwAjMwUzLwEzL4UzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]不管是複利的可怕還是宰相的狡猾,都是因為其中含有共同的關鍵因素——指數項 ,是指數項 的奇妙作用,使得看似簡單的事情令人吃驚。
古代指數(冪)發展
指數與冪的概念的形成是相當曲折和緩慢的指數符號( Sign of power) 的種類繁多,且記法多樣化。
我國古代“冪”字至少有十各不同的寫法。
劉徽為《九章算術》作注,在《方田》章求矩形面積法則中寫道:“此積謂田冪,凡廣從相乘謂之冪( 長和寬相乘的積叫作冪) 。”這是第一次在數學文獻上出現冪。
![指數[數學用語]](/img/1/645/wZwpmLwADOwgDMxMTMzEDN0UTMyITNykTO0EDMwAjMwUzLzEzLwUzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]《準南子·天文訓》講到樂律,有這樣幾句話:“故黃鐘之律九寸,而宮音調;因而九之,九九八十一,故黃鐘之有選舉權立焉......十二各以三成,故置一而十一三之,為積分十七萬七千一百四十七,黃鐘大數立焉。”可翻譯如下:發出黃鐘音律的管長 9寸,它的音調叫作宮。用 9 去乘它得81。81 這個數叫作黃鐘數。12 律的每一個是根據三分損益這個原則造成的。所以將 3 乘了11次,得到的積,分管長 177147等份,這177147 叫作黃鐘大數,以別於黃鐘數81。很明顯,“置一而十一三之”就是乘方運算,11 就是現在的指數。整句話包含式子,具有指數的初步概念。
1607 年,利瑪竇和徐光啟合譯歐幾里得的 《幾何原本》,在譯本中徐光啟重新使用了冪字,並有註解:“自乘之數曰冪。”這是第一次給冪這個概念下定義。
![指數[數學用語]](/img/6/56a/wZwpmLzEzN1ADN2cjN1IDN0UTMyITNykTO0EDMwAjMwUzL3YzL3EzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/a/034/wZwpmLwcDOyEzNyMTMzEDN0UTMyITNykTO0EDMwAjMwUzLzEzLwMzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/f/1b8/wZwpmLzcTOxEDO5ETN2IDN0UTMyITNykTO0EDMwAjMwUzLxUzL4UzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]![指數[數學用語]](/img/b/9c4/wZwpmL4EzN2gTOwkDO0ATN0UTMyITNykTO0EDMwAjMwUzL5gzLyczLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 指數[數學用語]
指數[數學用語]至十七世紀,具有“現代”意義的指數符號才出現。最初的,只是表示未知數之次數,但並無出現未知量符號。比爾吉則把羅馬數字寫於係數數字之上,以表示未知量次數。其後,克卜勒等亦採用了這符號。羅曼斯開始寫出未知量的字母。1631 年,哈里奧特( 1560-1621) 改進了韋達的記法,以 aa表示, 以aaa 表示。1636 年,居於巴黎的蘇格蘭人休姆( James Hume) 以小羅馬數字放於字母之右上角的方式表達指數,如以表示,該表示方式除了用的是羅馬數字外,已與現在的指數表示法相同。笛卡兒( 1596-1650) 以較小的印度阿拉伯數字放於右上角來表示指數,是現今通用的指數表示法。
![指數[數學用語] 指數[數學用語]](/img/e/339/nBnauM3XxQDM0QDMzYzM5IDN0UTMyITNykTO0EDMwAjMwUzL2MzLyczLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg)
