概念簡述
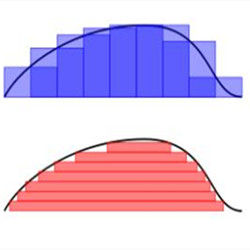
眾所周知,在里一個區域E的黎曼積分的幾何意義是分別用一個(即有限個)曲邊多邊形A和B去覆蓋和填充E,若inf{|A|}=sup{|B|},則稱E可積。而在套用中這在某種情況下面是不足夠的。所以勒貝格從“一個”曲邊多邊形出發,去更改積分的定義,把“一個”改為“可數個”,最終導致數學史上的第三次完備化——L可積函式的極限仍然是L可積的。
積分介紹
 勒貝格積分
勒貝格積分勒貝格從另一個角度來考慮積分概念,導致勒貝格積分和測度概念。比如計算面積,可以將小區間的高度(Y值)乘以對應的所有小區間的長度的和(測度),然後加起來。又比如現有硬幣:25,25,10,5,10,1,5,25。用黎曼積分來求和:25+25+10+5+10+1+5+25=106。用勒貝格積分來求和:25*3+10*2+5*2+1=106。結果是一樣的。但對於一些“壞”函式,結果是不一樣的。
比如在X軸[0,1]閉區間上定義函式:
Y=1,當X是有理數;
Y=0,當X是無理數。
求該函式覆蓋的面積。
黎曼積分無法定義,因為任意小的區間都包含無理數和有理數。
用勒貝格積分來求和:1*0+0*1=0。
[0,1]閉區間的長度(測度)是1;有限點集的長度(測度)是0;無限可數點集(如,有理數)的長度(測度)是0。而[0,1]閉區間的長度(測度)=有理數集的長度+無理數集的長度。
所以,[0,1]閉區間的無理數集的長度(測度)是1。這就解釋了上述計算結果。
還有物理學裡面常見的狄拉克δ函式,Riemann積分下是不可積的,在L積分意義下它有著最初物理學家所定義的性質。
由此可見,勒貝格積分比黎曼積分廣義。但必須指出,勒貝格積分無法完全代替黎曼積分,問題出在L可積函式具有絕對可積的性質,導致條件收斂的黎曼廣義可積函式不是L可積函式。
背景知識
 勒貝格積分
勒貝格積分1854年黎曼(德,1826-1866年)定義了黎曼積分,19世紀末,分析的嚴格化迫使許多數學家認真考慮所謂“病態函式”,特別是不連續函式、不可微函式的積分問題,如,積分的概念可以怎樣推廣到更廣泛的函式類上?1898年波萊爾(法,1871-1956年)的測度論(1925年曾任法國海軍部長),1902年勒貝格(法,1875-1941年)的博士論文《積分,長度與面積》建立了測度論和積分論,使一些原先在黎曼意義下不可積的函式按勒貝格的意義變得可積了,可以重建微積分基本定理,從而形成一門新的學科:實變函式論。成為分析的“分水嶺”,人們常把勒貝格以前的分析學稱為經典分析,而把以由勒貝格積分引出的實變函式論為基礎而開拓出來的分析學稱為現代分析。
黎曼積分的重要推廣,分析數學中普遍使用的重要工具。
19世紀的微積分學中已經有了許多直觀而有用的積分,例如黎曼積分(簡稱R積分)、黎曼-斯蒂爾傑斯積分(簡稱R-S積分)等。只要相應的函式性質良好,用這些積分來計算曲邊形面積、物體重心、物理學上的功、能等,是很方便的。然而,隨著認識的深入,人們愈來愈經常地需要處理複雜的函式,例如,由一列性質良好的函式組成級數所定義出來的函式,兩個變元的函式對一個變元積分後所得到的一元函式等。在討論它們的可積性、連續性、可微性時,經常遇到積分與極限能否交換順序的問題。通常只有在很強的假設下才能對這問題作出肯定的回答。因此,在理論和套用上都迫切要求建立一種新的積分,它既能保持R積分的幾何直觀和計算上的有效,又能在積分與極限交換順序的條件上有較大的改善。1902年法國數學家H.L.勒貝格出色地完成了這一工作,建立了以後人們稱之為勒貝格積分的理論,接著又綜合R-S積分思想產生了勒貝格-斯蒂爾傑斯積分(簡稱l-S積分)。20世紀初又發展成建立在一般集合上的測度和積分的理論,簡稱測度論。
勒貝格
(1875~1941)Lebesgue,HenriLon法國數學家。1875年6月28日生於博韋,1941年7月26日卒於巴黎。1894~1897年在巴黎高等師範學校學習。1902年在巴黎大學獲得博士學位,從1902年起先後在雷恩大學、普瓦蒂埃大學、巴黎大學文理學院任教。1922年任法蘭西學院教授,同年被選為巴黎科學院院士。
勒貝格的主要貢獻是測度和積分理論。他採用無窮個區間來覆蓋點集,使許多特殊的點集的測度有了定義。在定義積分時他也採取劃分值域而不是劃分定義域的辦法,使積分歸結為測度,從而使黎曼積分的局限性得到突破,進一步發展了積分理論。他的理論為20世紀的許多數學分支如泛函分析、機率論、抽象積分論、抽象調和分析等奠定了基礎。利用勒貝格積分理論,他對三角級數論也作出基本的改進。另外,他在維數論方面也有貢獻。晚年他對初等幾何學及數學史進行了研究。他的論文收集在《勒貝格全集》。