基本介紹
 互反函式
互反函式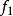 互反函式
互反函式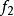 互反函式
互反函式在數學中,有好些運算是互逆的。加和減,乘和除,乘方和開方,都屬於這一類。一個自變數x,在經過一種運算之後得到y,再對這y進行相應的逆運算,結果是仍回到x。例如,以a乘x,得y =ax,將這y除以a,又得x,又如,將x平方,得再對y開平方,又得x。今以表示前一運算,以表示其逆運算,則上述關係可表示如下:
 互反函式
互反函式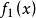 互反函式
互反函式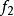 互反函式
互反函式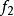 互反函式
互反函式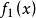 互反函式
互反函式 互反函式
互反函式將寫在後的方括弧內,就表示內的那個變數y當用代入。例如,它們就符合上述條件,理由是:
 互反函式
互反函式 互反函式
互反函式從的組成上看,它也是一種複合函式。對式(1)兩側求導,當有:
 互反函式
互反函式 互反函式
互反函式 互反函式
互反函式式中:——對y的導數;
 互反函式
互反函式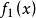 互反函式
互反函式——對x的導數;
1——x對x的導數。
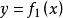 互反函式
互反函式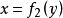 互反函式
互反函式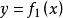 互反函式
互反函式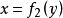 互反函式
互反函式 互反函式
互反函式 互反函式
互反函式 互反函式
互反函式 互反函式
互反函式 互反函式
互反函式在式(1)中,一個運算是用將x變成y,另一個運算是用將y變成x,在這條件下,和實際上是同一個方程,它們的圖形也是同一條曲線。以和為例,將後一式平方,得移除作乘,就得前一式。由此可見,若某個方程按對y求導要比對x求導方便,其切線的斜率y' (式(2)中的) 也可用x' (式(2)中的) 的倒數表示;即:
 互反函式
互反函式 互反函式
互反函式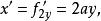 互反函式
互反函式例如,所給的式子是則於是,
 互反函式
互反函式 互反函式
互反函式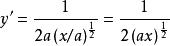 互反函式
互反函式 互反函式
互反函式 互反函式
互反函式 互反函式
互反函式若將代人,。而在將化為再求導時,結果是相符的。但用式(B)來表示y',時常較為簡捷。
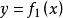 互反函式
互反函式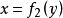 互反函式
互反函式 互反函式
互反函式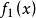 互反函式
互反函式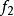 互反函式
互反函式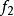 互反函式
互反函式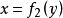 互反函式
互反函式 互反函式
互反函式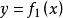 互反函式
互反函式 互反函式
互反函式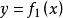 互反函式
互反函式 互反函式
互反函式既然和在圖上是同一條線,那就容易混淆。又因是表示將作為內的變數代人,至於內的變數原先是用什麼字母來代表,那卻沒有多大關係。因此,常改作這也就是將原給的內的x和y對換,而後變形為。這樣的和就叫 互反函式 。
冪函式的反函式
利用互反函式的這一對稱性質來看冪函式,將見:
 互反函式
互反函式 互反函式
互反函式 互反函式
互反函式(1) 每一個冪函式的反函式仍是一個冪函式,因此,冪函式組成一個自反的函式族。這就是說,的反函式是(且後式也可寫作),而它們都是冪函式。
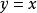 互反函式
互反函式(2)指數是真分數的冪函式,它的反函式(也是冪函的指數就大於1(是原來那個真分數的倒數)。由於指數大於1的冪函式的描點製圖較易進行,可以先將反函式圖形作出,再利用原函式和反函式對直線的對稱,原函式作出 。

