原函式:原函式是指對於一個定義在某區間的已知函式f(x)，如果存在可導函 -百科知識中文網

定義

已知函式f(x)是一個定義在某區間的函式，如果存在可導函式F(x)，使得在該區間內的任一點都有dF(x)=f(x)dx，則在該區間內就稱函式F(x)為函式f(x)的原函式。

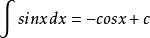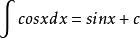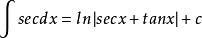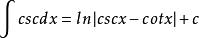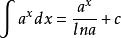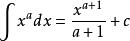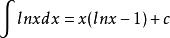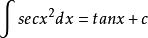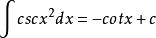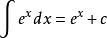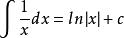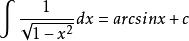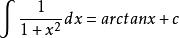例如：sinx是cosx的原函式。

其中，c均為任意常數。

若函式f(x)在某區間上連續，則f(x)在該區間內必存在原函式，這是一個充分而不必要條件，也稱為“原函式存在定理”。

函式族F(x)+C(C為任一個常數）中的任一個函式一定是f(x)的原函式，

故若函式f(x)有原函式，那么其原函式為無窮多個。

例如：x 是3x 的一個原函式，易知，x +1和x +2也都是3x 的原函式。因此，一個函式如果有一個原函式，就有許許多多原函式，原函式概念是為解決求導和微分的逆運算而提出來的。

例如：已知作直線運動的物體在任一時刻t的速度為v=v(t),要求它的運動規律，就是求v=v(t)的原函式。原函式的存在問題是微積分學的基本理論問題，當f(x)為連續函式時，其原函式一定存在。

設f(x)在[a,b]上連續，則由曲線y=f(x)，x軸及直線x=a，x=b圍成的曲邊梯形的面積函式(指代數和——x軸上方取正號，下方取負號)是f(x)的一個原函式.若x為時間變數，f(x)為直線運動的物體的速度函式，則f(x)的原函式就是路程函式。