概述
三角函式的反函式，是多值函式。它們是反正弦arcsin x，反餘弦arccos x，反正切Arctan x，反餘切arccot x，反正割arcsec x，反餘割Arccsc x等，各自表示其正弦、餘弦、正切、餘切、正割、餘割為x的角。
相關介紹
為限制反三角函式為單值函式，將反正弦函式的值y限在y=-π/2≤y≤π/2，將y為反正弦函式的主值，記為y=arcsin x；相應地，反餘弦函式y=arccos x的主值限在0≤y≤π；反正切函式y=arctan x的主值限在-π/2
分類
三角函式的反函式不是單值函式，因為它並不滿足一個自變數對應一個函式值的要求，其圖像與其原函式關於函式y=x對稱。歐拉提出反三角函式的概念，並且首先使用了“arc+函式名”的形式表示反三角函式，而不是。
為限制反三角函式為單值函式，將反正弦函式的值y限在-π/2≤y≤π/2，將y作為反正弦函式的主值，記為y=arcsinx；相應地，反餘弦函式y=arccosx的主值限在0≤y≤π；反正切函式y=arctanx的主值限在-π/2<y<π/2；反餘切函式y=arccotx的主值限在0<y<π。
反正弦函式
y=sinx在[-π/2，π/2]上的反函式，叫做反正弦函式。記作arcsinx，表示一個正弦值為x的角，該角的範圍在[-π/2，π/2]區間內。定義域[-1，1]，值域[-π/2，π/2]。
反餘弦函式
y=cosx在[0，π]上的反函式，叫做反餘弦函式。記作arccosx，表示一個餘弦值為x的角，該角的範圍在[0，π]區間內。定義域[-1，1]，值域[0，π]。
綠的為y=arccos(x)紅的為y=arcsin(x)
綠的為y=arccos(x)紅的為y=arcsin(x)
反正切函式
y=tanx在(-π/2，π/2）上的反函式，叫做反正切函式。記作arctanx，表示一個正切值為x的角，該角的範圍在（-π/2，π/2）區間內。定義域R，值域（-π/2，π/2）。
反餘切函式
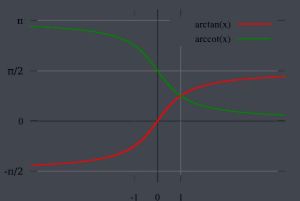綠的為y=arccot(x) 紅的為y=arctan(x)綠的為y=arccot(x)紅的為y=arctan(x)
綠的為y=arccot(x)紅的為y=arctan(x)
反正割函式
y=secx在[0,π/2)U(π/2,π]上的反函式，叫做反正割函式。記作arcsecx，表示一個正割值為x的角，該角的範圍在[0,π/2)U(π/2,π]區間內。定義域（-∞,-1]U[1,+∞),值域[0,π/2)U(π/2,π]。
反餘割函式
y=cscx在[-π/2,0)U(0,π/2]上的反函式，叫做反餘割函式。記作arccscx，表示一個餘割值為x的角，該角的範圍在[-π/2,0)U(0,π/2]區間內。定義域（-∞,-1]U[1,+∞),值域[-π/2,0)U(0,π/2]。
數學公式
基本
secant（正割）Sec(X)=1/Cos(X)
cosecant（餘割）Cosec(X)=1/Sin(X)
cotangent（餘切）Cotan(X)=1/Tan(X)
InverseSine（反正弦）Arcsin(X)=Atn(X/Sqr(-X*X+1))
InverseSecant（反正割）Arcsec(X)=Atn(X/Sqr(X*X-1))+Sgn((X)-1)*(2*Atn(1))
InverseCosecant（反餘割）Arccosec(X)=Atn(X/Sqr(X*X-1))+(Sgn(X)-1)*(2*Atn(1))
InverseCotangent（反餘切）Arccotan(X)=Atn(X)+2*Atn(1)
其他公式
cos(arcsinx)=(1-x^2)^0.5
arcsin(-x)=-arcsinx
arccos(-x)=π-arccosx
arctan(-x)=-arctanx
arccot(-x)=π-arccotx
arcsinx+arccosx=π/2=arctanx+arccotx
sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x
arcsinx=x+x^3/(2*3)+(1*3)x^5/(2*4*5)+1*3*5(x^7)/(2*4*6*7）……+(2k+1)!!*x^(2k-1)/(2k!!*(2k+1))+……（|x|<1)!！表示雙階乘
arccosx=π-(x+x^3/(2*3)+(1*3)x^5/(2*4*5)+1*3*5(x^7)/(2*4*6*7）……）（|x|<1)
arctanx=x-x^3/3+x^5/5-……
舉例
當x∈[-π/2，π/2]有arcsin(sinx)=x
x∈[0，π]，arccos(cosx)=x
x∈（-π/2，π/2），arctan(tanx)=x
x∈（0，π），arccot(cotx)=x
x>0，arctanx=π/2-arctan1/x，arccotx類似
若(arctanx+arctany）∈（-π/2，π/2），則arctanx+arctany=arctan((x+y)/(1-xy))
例如，arcsinχ表示角α，滿足α∈[-π/2，π/2]且sinα=χ;arccos(-4/5)表示角β，滿足β∈[0，π]且cosβ=-4/5;arctan2表示角φ，滿足φ∈（-π/2，π/2)且tanφ=2
數學術語
為限制反三角函式為單值函式，將反正弦函式的值y限在y=-π/2≤y≤π/2，將y為反正弦函式的主值，記為y=arcsinx；相應地，反餘弦函式y=arccosx的主值限在0≤y≤π；反正切函式y=arctanx的主值限在-π/2<y<π/2；反餘切函式y=arccotx的主值限在0<y<π。
反三角函式實際上並不能叫做函式，因為它並不滿足一個自變數對應一個函式值的要求，其圖像與其原函式關於函式y=x對稱。其概念首先由歐拉提出，並且首先使用了arc+函式名的形式表示反三角函式，而不是f-1(x).
（1）正弦函式y=sinx在[-π/2,π/2]上的反函式，叫做反正弦函式。arcsinx表示一個正弦值為x的角，該角的範圍在[-π/2,π/2]區間內。
（2）餘弦函式y=cosx在[0,π]上的反函式，叫做反餘弦函式。arccosx表示一個餘弦值為x的角，該角的範圍在[0,π]區間內。
（3）正切函式y=tanx在(-π/2,π/2)上的反函式，叫做反正切函式。arctanx表示一個正切值為x的角，該角的範圍在(-π/2,π/2)區間內。
反三角函式主要是三個：
y＝arcsin(x)，定義域[-1,1]，值域[-π/2,π/2]圖象用紅色線條；
y=arccos(x)，定義域[-1,1]，值域[0,π]，圖象用藍色線條；
y=arctan(x)，定義域(-∞,+∞)，值域(-π/2,π/2)，圖象用綠色線條；
y=arccot(x)，定義域(-∞,+∞)，值域(0,π)，圖象用綠色線條；
sin(arcsinx)=x,定義域[-1,1],值域[-1,1]arcsin(-x)=-arcsinx
證明方法如下：設arcsin(x)=y,則sin(y)=x,將這兩個式子代入上式即可得
其他幾個用類似方法可得
cos(arccosx)=x,arccos(-x)=π-arccosx
tan(arctanx)=x,arctan(-x)=-arctanx
