arc[反函式符號前綴]

ARC是數學中的一個基本符號，常寫於等號“=”之後，代表等號後的函式為等號前函式的反函式.也常運用於物理運算和幾何運算。

基本公式與概述

正弦函式和它的反函式：f(x)=sinx->f(x)=arcsinx

餘弦函式和它的反函式：f(x)=cosx->f(x)=arccosx

正切函式和它的反函式：f(x)=tanx->f(x)=arctanx

餘切函式和它的反函式：f(x)=cotx->f(x)=arccotx

數學裡arc是反三角函式的符號，適用於表達不特殊的角的大小，我們知道特殊角如30°的tan值，sin值和cos值都是一個特殊的數，但是在解決一些題的時候會出現某一個角的三角函式值不特殊，我們又沒有反三角函式表，所以不清楚這個角的大小，arc的作用就是表示這種不特殊的角,其中涉及增減性的問題。

反三角函式

概述

反三角函式是一種基本初等函式。它並不能狹義的理解為三角函式的反函式，是個多值函式。它是反正弦arcsin x，反餘弦arccos x，反正切arctan x，反餘切arccot x這些函式的統稱，各自表示其正弦、餘弦、正切、餘切為x的角。

分類

arc[反函式符號前綴]

三角函式的反函式不是單值函式，因為它並不滿足一個自變數對應一個函式值的要求，其圖像與其原函式關於函式y=x對稱。歐拉提出反三角函式的概念，並且首先使用了“arc+函式名”的形式表示反三角函式，而不是。

為限制反三角函式為單值函式，將反正弦函式的值y限在-π/2≤y≤π/2，將y作為反正弦函式的主值，記為y=arcsin x；相應地，反餘弦函式y=arccos x的主值限在0≤y≤π；反正切函式y=arctan x的主值限在-π/2<y<π/2；反餘切函式y=arccot x的主值限在0<y<π。

反正弦函式

y=sin x在[-π/2，π/2]上的反函式，叫做反正弦函式。記作arcsinx，表示一個正弦值為x的角，該角的範圍在[-π/2，π/2]區間內。定義域[-1，1] ，值域[-π/2，π/2]。

反餘弦函式

y=cos x在[0，π]上的反函式，叫做反餘弦函式。記作arccosx，表示一個餘弦值為x的角，該角的範圍在[0，π]區間內。定義域[-1，1] ， 值域[0，π]。

反正切函式

y=tan x在(-π/2，π/2）上的反函式，叫做反正切函式。記作arctanx，表示一個正切值為x的角，該角的範圍在（-π/2，π/2）區間內。定義域R，值域（-π/2，π/2）。

反餘切函式

y=cot x在（0，π）上的反函式，叫做反餘切函式。記作arccotx，表示一個餘切值為x的角，該角的範圍在（0，π）區間內。定義域R，值域（0，π）。

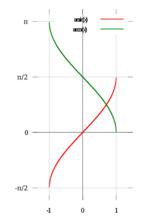綠的為y=arccot(x) 紅的為y=arctan(x)

反正割函式

y=sec x在[0,π/2)U(π/2,π]上的反函式，叫做反正割函式。記作arcsecx，表示一個正割值為x的角，該角的範圍在[0,π/2)U(π/2,π]區間內。定義域（-∞,-1]U[1,+∞),值域[0,π/2)U(π/2,π]。

反餘割函式

y=csc x在[-π/2,0)U(0,π/2]上的反函式，叫做反餘割函式。記作arccscx，表示一個餘割值為x的角，該角的範圍在[-π/2,0)U(0,π/2]區間內。定義域（-∞,-1]U[1,+∞),值域[-π/2,0)U(0,π/2]。