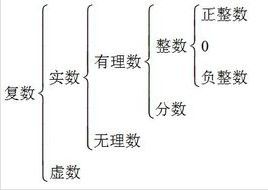
基本概念
實數實數可以分為有理數和無理數（如π、√2）兩類，或代數數和超越數兩類，或正數，負數和零三類。實數集合通常用字母'R'表示。而Rn表示n維實數空間。實數是不可數的。實數是實分析的核心研究對象。
實數可以用來測量連續的量。理論上，任何實數都可以用無限小數的方式表示，小數點的右邊是一個無窮的數列（可以是循環的，也可以是非循環的）。在實際運用中，實數經常被近似成一個有限小數（保留小數點後n位，n為正整數）。在計算機領域，由於計算機只能存儲有限的小數位數，實數經常用浮點數來表示。
1°相反數（只有符號不同的兩個數，它們的和為零，我們就說其中一個是另一個的相反數）實數a的相反數記作-a，a和-a在數軸上到原點0的距離相等。）
2°絕對值（在數軸上另一個數與a到原點0的距離分別相等）實數a的絕對值記作：|a|
①a為正數時，|a|=a（不變）
②a為0時，|a|=0
③a為負數時，|a|=-a（即數a的相反數）
(任何數的絕對值都大於或等於0，因為距離沒有負的。)
3°倒數（兩個實數的乘積是1，則這兩個數互為倒數）實數a的倒數是：1/a（a≠0）。0沒有倒數。
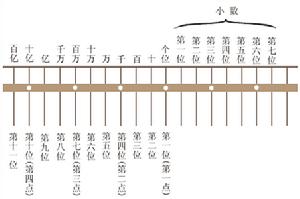
4°數軸（任何實數都可在數軸上表示。）
定義：如果畫一條直線，規定向右的方向為直線的正方向，在其上取原點O及單位長度OE，它就成為數軸線，或稱數軸。
（1）數軸的三要素：原點、正方向和單位長度。
（2）數軸上的點與實數一一對應。[1]
5°平方根（在實數系中如果某個數x自乘結果等於a，即x²=a，那么x就是a的平方根；如果上述的x是非負的，便稱x為a的算術平方根。算術平方根可用√￣表示。一個正數有兩個平方根；0隻有一個平方根，就是0本身；負數在實數系中沒有平方根。）
6°立方根（如果一個數x的立方等於a，即x³=a，即3個x連續相乘等於a，那么這個數x就叫做a的立方根（cuberoot），也叫做三次方根。實數系中，立方根的符號為∛￣。）
歷史
埃及人早在大約公元前1000年就開始運用分數了。在公元前500年左右，以畢達哥拉斯為首的希臘數學家們意識到了無理數存在的必要性。印度人於公元600年左右發明了負數，據說中國也曾發明負數，但稍晚於印度。
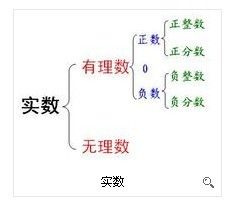實數在公元前500年左右，以畢達哥拉斯為首的希臘數學家們認識到有理數在幾何上不能滿足需要，但畢達哥拉斯本身並不承認無理數的存在。直到17世紀，實數才在歐洲被廣泛接受。18世紀，微積分學在實數的基礎上發展起來。1871年，德國數學家康托爾第一次提出了實數的嚴格定義。
根據日常經驗，有理數集在數軸上似乎是“稠密”的，於是古人一直認為用有理數即能滿足測量上的實際需要。以邊長為1厘米的正方形為例，其對角線有多長？在規定的精度下（比如誤差小於0.001厘米），總可以用有理數來表示足夠精確的測量結果（比如1.414厘米）。但是，古希臘畢達哥拉斯學派的數學家發現，只使用有理數無法完全精確地表示這條對角線的長度，這徹底地打擊了他們的數學理念；他們原以為：
任何兩條線段（的長度）的比，可以用自然數的比來表示。
正因如此，畢達哥拉斯本人甚至有“萬物皆數”的信念，這裡的數是指自然數（1,2,3，...），而由自然數的比就得到所有正有理數，而有理數集存在“縫隙”這一事實，對當時很多數學家來說可謂極大的打擊；見第一次數學危機。
從古希臘一直到17世紀，數學家們才慢慢接受無理數的存在，並把它和有理數平等地看作數；後來有虛數概念的引入，為加以區別而稱作“實數”，意即“實在的數”。在當時，儘管虛數已經出現並廣為使用，實數的嚴格定義卻仍然是個難題，以至函式、極限和收斂性的概念都被定義清楚之後，才由十九世紀末的戴德金、康托等人對實數進行了嚴格處理。
相關定義
從有理數構造實數
實數可以用通過收斂於一個唯一實數的十進制或二進制展開如{3,3.1,3.14,3.141,3.1415,…}所定義的序列的方式而構造為有理數的補全。實數可以不同方式從有理數構造出來。這裡給出其中一種，其他方法請詳見實數的構造。
公理的方法
設R是所有實數的集合，則：
集合R是一個域：可以作加、減、乘、除運算，且有如交換律，結合律等常見性質。
域R是個有序域，即存在全序關係≥，對所有實數x,y和z：
若 x≥y 則 x+z≥y+z；
若 x≥0 且 y≥0 則 x'y≥0。
集合R滿足戴德金完備性，即任意R的非空子集S(S⊆R,S≠∅)，若S在R內有上界，那么S在R內有上確界。
最後一條是區分實數和有理數的關鍵。例如所有平方小於2的有理數的集合存在有理數上界，如1.5；但是不存在有理數上確界（因為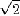
不是有理數）。
實數通過上述性質唯一確定。更準確的說，給定任意兩個戴德金完備的有序域R1和R2，存在從R1到R2的唯一的域同構，即代數學上兩者可看作是相同的。
【性質與概念】
基本概念
實數可以分為有理數和無理數兩類，或代數數和超越數兩類，或正實數，負實數和零三類。實數集合通常用字母R表示。而R^n表示n維實數空間。實數是不可數的。實數是實數理論的核心研究對象。
實數可以用來測量連續的量。理論上，任何實數都可以用無限小數的方式表示，小數點的右邊是一個無窮的數列(可以是循環的，也可以是非循環的)。在實際運用中，實數經常被近似成一個有限小數(保留小數點後n位，n為正整數，包括整數)。在計算機領域，由於計算機只能存儲有限的小數位數，實數經常用浮點數來表示。
1)相反數(只有符號不同的兩個數，它們的和為零，我們就說其中一個是另一個的相反數)實數a的相反數是-a，a和-a在數軸上到原點0的距離相等。)
2)絕對值(在數軸上另一個數與a到原點0的距離分別相等)實數a的絕對值是：|a|
①a為正數時，|a|=a(不變)
②a為0時，|a|=0
③a為負數時，|a|=-a(為a的相反數)
(任何數的絕對值都大於或等於0，因為距離沒有負的。)
3)倒數(兩個實數的乘積是1，則這兩個數互為倒數)實數a的倒數是：1/a(a≠0)
4)數軸(任何實數都可在數軸上表示。)
定義：如果畫一條直線，規定向右的方向為直線的正方向，在其上取原點O及單位長度OE，它就成為數軸線，或稱數軸。
(1)數軸的三要素：原點、正方向和單位長度。
(2)數軸上的點與實數一一對應。
5)平方根(某個自乘結果等於的實數，表示為〔√￣〕，其中屬於非負實數的平方根稱算術平方根。一個正數有兩個平方根;0隻有一個平方根，就是0本身;負數沒有平方根。)
6)立方根(如果一個數x的立方等於a，即x的三次方等於a(x^3=a)，即3個x連續相乘等於a,那么這個數x就叫做a的立方根(cuberoot)，也叫做三次方根)
分類
實數按性質分類是：正實數、負實數、0
實數按定義分類是：有理數、無理數
有理數的分類可以分為整數,分數
整數又可分為正整數,0,負整數
分數又可分為正分數,負分數
正有理數又可分為正整數,正分數
負有理數又可分為負整數,負分數
無理數可分為正無理數和負無理數。
例子
15(整數)2.121(有限小數)
1.3333333...(無限循環小數)
π=3.1415926...(無限不循環小數)
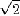(無理數)
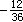(分數)相關性質
基本運算
實數可實現的基本運算有加、減、乘、除、平方等，對非負數還可以進行開方運算。實數加、減、乘、除（除數不為零）、平方後結果還是實數。任何實數都可以開奇次方，結果仍是實數，只有非負實數，才能開偶次方其結果還是實數。四則運算封閉性
實數集R對加、減、乘、除（除數不為零）四則運算具有封閉性，即任意兩個實數的和、差、積、商（除數不為零）仍然是實數。有序性
實數集是有序的，即任意兩個實數a、b必定滿足下列三個關係之一：a<b，a=b，a>b。傳遞性
實數大小具有傳遞性，即若a>b，且b>c，則有a>c。阿基米德性質
實數具有阿基米德性質（Archimedeanproperty），即∀a，b∈R，若a>0，則∃正整數n，na>b。稠密性
實數集R具有稠密性，即兩個不相等的實數之間必有另一個實數，既有有理數，也有無理數.數軸
如果在一條直線（通常為水平直線）上確定O作為原點，指定一個方向為正方向（通常把指向右的方向規定為正方向），並規定一個單位長度，則稱此直線為數軸。任一實數都對應與數軸上的唯一一個點；反之，數軸上的每一個點也都唯一的表示一個實數。於是，實數集R與數軸上的點有著一一對應的關係。完備性
作為度量空間或一致空間，實數集合是個完備空間，它有以下性質：所有實數的柯西序列都有一個實數極限。
有理數集合就不是完備空間。例如，(1,1.4,1.41,1.414,1.4142,1.41421,...)是有理數的柯西序列，但沒有有理數極限。實際上，它有個實數極限
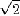。實數是有理數的完備化——這亦是構造實數集合的一種方法。極限的存在是微積分的基礎。實數的完備性等價於歐幾里德幾何的直線沒有“空隙”。
完備的有序域
實數集合通常被描述為“完備的有序域”，這可以幾種解釋。
* 首先，有序域可以是完備格。然而，很容易發現沒有有序域會是完備格。這是由於有序域沒有最大元素（對任意元素z，z+1將更大）。所以，這裡的“完備”不是完備格的意思。
* 另外，有序域滿足戴德金完備性，這在上述公理中已經定義。上述的唯一性也說明了這裡的“完備”是指戴德金完備性的意思。這個完備性的意思非常接近採用戴德金分割來構造實數的方法，即從（有理數）有序域出發，通過標準的方法建立戴德金完備性。
* 這兩個完備性的概念都忽略了域的結構。然而，有序群（域是種特殊的群）可以定義一致空間，而一致空間又有完備空間的概念。上述完備性中所述的只是一個特例。（這裡採用一致空間中的完備性概念，而不是相關的人們熟知的度量空間的完備性，這是由於度量空間的定義依賴於實數的性質。）當然，R並不是唯一的一致完備的有序域，但它是唯一的一致完備的阿基米德域。實際上，“完備的阿基米德域”比“完備的有序域”更常見。可以證明，任意一致完備的阿基米德域必然是戴德金完備的（當然反之亦然）。這個完備性的意思非常接近採用柯西序列來構造實數的方法，即從（有理數）阿基米德域出發，通過標準的方法建立一致完備性。
* “完備的阿基米德域”最早是由希爾伯特提出來的，他還想表達一些不同於上述的意思。他認為，實數構成了最大的阿基米德域，即所有其他的阿基米德域都是R的子域。這樣R是“完備的”是指，在其中加入任何元素都將使它不再是阿基米德域。這個完備性的意思非常接近用超實數來構造實數的方法，即從某個包含所有（超實數）有序域的純類出發，從其子域中找出最大的阿基米德域。
高級性質
* 實數集是不可數的，也就是說，實數的個數嚴格多於自然數的個數（儘管兩者都是無窮大）。這一點，可以通過康托爾對角線方法證明。實際上，實數集的勢為2ω（請參見連續統的勢），即自然數集的冪集的勢。由於實數集中只有可數集個數的元素可能是代數數，絕大多數實數是超越數。實數集的子集中，不存在其勢嚴格大於自然數集的勢且嚴格小於實數集的勢的集合，這就是連續統假設。該假設不能被證明是否正確，這是因為它和集合論的公理不相關。* 所有非負實數的平方根屬於R，但這對負數不成立。這表明R上的序是由其代數結構確定的。而且，所有奇數次多項式至少有一個根屬於R。這兩個性質使R成為實封閉域的最主要的實例。證明這一點就是對代數基本定理的證明的前半部分。
* 實數集擁有一個規範的測度，即勒貝格測度。
* 實數集的上確界公理用到了實數集的子集，這是一種二階邏輯的陳述。不可能只採用一階邏輯來刻畫實數集：1.Löwenheim-Skolem定理說明，存在一個實數集的可數稠密子集，它在一階邏輯中正好滿足和實數集自身完全相同的命題；2.超實數的集合遠遠大於R，但也同樣滿足和R一樣的一階邏輯命題。滿足和R一樣的一階邏輯命題的有序域稱為R的非標準模型。這就是非標準分析的研究內容，在非標準模型中證明一階邏輯命題（可能比在R中證明要簡單一些），從而確定這些命題在R中也成立。
拓撲性質
實數集構成一個度量空間：x和y間的距離定為絕對值|x-y|。作為一個全序集，它也具有序拓撲。這裡，從度量和序關係得到的拓撲相同。實數集又是1維的可縮空間（所以也是連通空間）、局部緊緻空間、可分空間、貝利空間。但實數集不是緊緻空間。這些可以通過特定的性質來確定，例如，無限連續可分的序拓撲必須和實數集同胚。以下是實數的拓撲性質總覽：i.令a為一實數。a的鄰域是實數集中一個包括一段含有a的線段的子集。
ii.R是可分空間。
iii.Q在R中處處稠密。
iv.R的開集是開區間的聯集。
v.R的緊子集是有界閉集。特別是：所有含端點的有限線段都是緊子集。
vi.每個R中的有界序列都有收斂子序列。
vii.R是連通且單連通的。
viii.R中的連通子集是線段、射線與R本身。由此性質可迅速導出中間值定理。
擴展與一般化
實數集可以在幾種不同的方面進行擴展和一般化：
* 最自然的擴展可能就是複數了。複數集包含了所有多項式的根。但是，複數集不是一個有序域。
* 實數集擴展的有序域是超實數的集合，包含無窮小和無窮大。它不是一個阿基米德域。
* 有時候，形式元素+∞和-∞加入實數集，構成擴展的實數軸。它是一個緊緻空間，而不是一個域，但它保留了許多實數的性質。
正因如此，畢達哥拉斯本人甚至有“萬物皆數”的信念，這裡的數是指自然數1,2,3...，而由自然數的比就得到所有正有理數，而有理數集存在“縫隙”這一事實，對當時很多數學家來說可謂極大的打擊；見第一次數學危機。
從古希臘一直到十七世紀，數學家們才慢慢接受無理數的存在，並把它和有理數平等地看作數；後來有虛數概念的引入，為加以區別而稱作“實數”，意即“實在的數”。在當時，儘管虛數已經出現並廣為使用，實數的嚴格定義卻仍然是個難題，以至函式、極限和收斂性的概念都被定義清楚之後，才由十九世紀末的戴德金、康托等人對實數進行了嚴格處理。
