定義
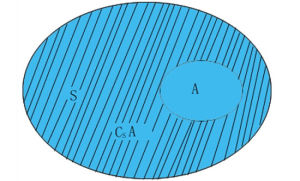 補集
補集絕對補集:若給定全集S,有A⊆S,則A在S中的相對補集稱為A的絕對補集(或簡稱補集),寫作∁SA。
注意:學習補集的概念,首先要理解全集的相對性,補集符號∁SA有三層含義:
A是U的一個子集,即A⊊U;
∁SA表示一個集合,且∁UA⊊U;
∁SA是由S中所有不屬於A的元素組成的集合,∁SA與A沒有公共元素,U中的元素分布在這兩個集合中;
全集是一個相對的概念,只包含所研究問題中所涉及的所有元素,補集只相對於相應的全集而言,如:我們在整數範圍內研究問題,則Z為全集,而當問題拓展到實數集時,則R為全集,補集也只是相對於此而言。
相關運算
求補律集合德·摩根定律
(“交之補”等於“補之並”)
(“並之補”等於“補之交”)
重點提示
學習補集的概念,首先要理解全集的相對性,補集符號∁s∪A有三層含義:①.A是U的一個子集,即A包含於U;
②.∁s∪A表示一個集合,且∁∪A包含於U;
③.∁s∪A是由U中所有不屬於A的元素組成的集合,∁s∪A與A沒有公共元素,U中的元素分布在∁s∪A與A這兩個集合中;
④.全集是一個相對的概念,只包含所研究問題中所涉及的所有元素,補集只想對於相應的全集而言,如:我們在整數範圍內研究問題,則Z為全集,而當問題拓展到實數集時,則R為全集,補集也只是相對於此而言。