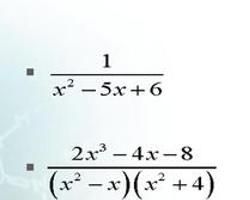概念
定義
形如 A/B(A、B是整式,B中含有字母)的式子叫做分式。其中A叫做分式的分子,B叫做分式的分母。
 分式
分式注意:判斷一個式子是否是分式,不要看式子是否是A/ B的形式,關鍵要滿足:分式的分母中必須含有字母,分子分母均為整式。無需考慮該分式是否有意義,即分母是否為零。
由於字母可以表示不同的數,所以分式比分數更具有一般性。
方法:數看結果,式看形。
分式條件
1.分式有意義條件:分母不為0。
2.分式值為0條件:分子為0且分母不為0。
3.分式值為正(負)數條件:分子分母同號得正,異號得負。
4.分式值為1的條件:分子=分母≠0。
5.分式值為-1的條件:分子分母互為相反數,且都不為0。
代數式分類
整式和分式統稱為有理式。
帶有根號且根號下含有字母的式子叫做無理式。
無理式和有理式統稱代數式。
分式的基本性質
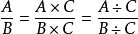 分式
分式分式的分子和分母同時乘以(或除以)同一個不為0的整式,分式的值不變。用式子表示為:
(A,B,C為整式,且B、C≠0)
運算法則
約分
根據分式基本性質,可以把一個分式的分子和分母的公因式約去,這種變形稱為分式的約分。約分的關鍵是確定分式中分子與分母的公因式。
約分步驟:1.如果分式的分子和分母都是單項式或者是幾個因式乘積的形式,將它們的公因式約去。
2.分式的分子和分母都是多項式,將分子和分母分別分解因式,再將公因式約去。
公因式的提取方法:係數取分子和分母係數的最大公約數,字母取分子和分母共有的字母,指數取公共字母的最小指數,即為它們的公因式。
最簡分式:一個分式不能約分時,這個分式稱為最簡分式。約分時,一般將一個分式化為最簡分式。
| | 1 | 2 | 3 |
| 單項式/單項式 | 提公因式 | 約去公因式 | 結果 |
| 多項式/多項式 | 因式分解 | 提公因式 | 結果 |
| 單項式/多項式 | 因式分解 | 提公因式 | 結果 |
通分
根據分數的基本性質,異分母的分數可以通分,使幾個分數的的分母相同;同樣,根據分式的基本性質,分式也可以進行類似的變形,使幾個異分母分式的分母相同,而分式的值不變。
通分:把幾個異分母分式分別化為與原分式值相等的同分母分式,叫做分式的通分。它與約分是互逆運算。
通分步驟:先求出所有分式分母的最簡公分母,再將所有分式的分母變為最簡公分母。同時各分式按照分母所擴大的倍數,相應擴大各自的分子。
最簡公分母的確定方法:係數取各因式係數的最低公倍數,相同字母的最高次冪及單獨字母的冪的乘積。
同分母加減
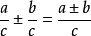 分式
分式同分母的分式相加減,分母不變,分子相加減。用字母表示為:
。
異分母加減
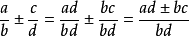 分式
分式異分母的分式相加減,通分化為同分母的分式,然後再按同分母分式的加減法法則進行計算。用字母表示為:
。
乘法
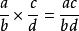 分式
分式兩個分式相乘,把分子相乘的積作為積的分子,把分母相乘的積作為積的分母。用字母表示為:
。
除法
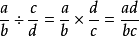 分式
分式兩個分式相除,把除式的分子和分母顛倒位置後再與被除式相乘:
。
也可表述為:除以一個分式,等於乘以這個分式的倒數。
乘方
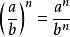 分式
分式分子乘方做分子,分母乘方做分母,可以約分的約分,最後化成最簡:
。
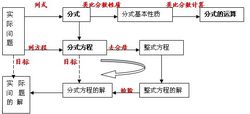
分式方程
基本簡介
分母中含有未知數的方程叫做分式方程。
解法介紹
初二數學,分式方程(免費)科科通按課文順序北師大版呂文華.flv
 分式
分式①去分母{方程兩邊同時乘以最簡公分母(最簡公分母:①係數取最低公倍數;②出現的字母取最高次冪;③出現的因式取最高次冪),將分式方程化為整式方程;若遇到互為相反數時。不要忘了改變符號};
②按解整式方程的步驟(移項,若有括弧應去括弧,注意變號,合併同類項, 係數化為1)求出未知數的值;
③驗根(求出未知數的值後必須驗根,因為在把分式方程化為整式方程的過程中,擴大了未知數的取值範圍,可能產生增根)。
一般地驗根,只需把整式方程的根代入最簡公分母,如果最簡公分母等於0,這個根就是增根,否則這個根就是原分式方程的根。若解出的根是增根,則原方程無解。
如果分式本身約分了,也要代進去檢驗。
基本步驟
(1)設未知數:若把題目中要求的未知數直接用字母表示出來,則稱為直接設未知數,否則稱間接設未知數;
(2)列代數式:用含未知數的代數式把題目中有關的量表示出來,必要時作出示意圖或列成表格,幫助理順各個量之間的關係;
(3)列出方程:根據題目中明顯的或者隱含的相等關係列出方程;
(4)解方程並檢驗;
(5)寫出答案。
在列分式方程解套用題時,不僅要檢驗所的解是否滿足方程式,還要檢驗它是否符合題意。
一般地,解分式方程時,去分母后所得整式方程的解有可能使原方程中分母為零,因此要將整式方程的解代入最簡公分母,如果最簡公分母的值不為零,則是方程的解。
分式方程及其套用舉例
例1:解方程(1)x/(x+1)=2x/(3x+3)+1
兩邊乘3(x+1)去分母得
3x=2x+(3x+3)
3x=5x+3
2x=-3
∴x=-3/2
經檢驗,x=-3/2是原方程的解
(2)2/(x-1)=4/(x^2-1)
兩邊乘(x+1)(x-1)去分母得
2(x+1)=4
2x+2=4
2x=2
∴x=1
檢驗 :把x=1帶入原方程,使分母為0,是增根。
故原方程2/(x-1)=4/(x^2-1 )無解 。
(3)2x-3+1/(x-5)=x+2+1/(x-5)
兩邊同時減1/(x-5),得x=5
代入原方程,使分母為0,所以x=5是增根
即方程無解!
檢驗:把x=a 帶入最簡公分母,若x=a使最簡公分母為0,則a是原方程的增根。若x=a使最簡公分母不為零, 則a是原方程的根。
歸納:解分式方程的基本思路是將分式方程化為整式方程,具體做法是“去分母”,即方程
兩邊同乘最簡公分母,這也是解分式方程的一般思路和做法。 檢驗格式:把x=a 帶入最簡公分母,若x=a使最簡公分母為0,則a是原方程的增根.若x=a使最簡公分母不為零,則a是原方程的根。
當然我們可憑經驗判斷是否有解。若有解,代入所有分母計算:若無解,代入無解分母即可。
例2:(2010湖南邵陽)小明離家2.4千米的體育館看球賽,進場時,發現門票還放在家中,此時離比賽還有45分鐘,於是他立即步行(勻速)回家取票,在家取票用時2分鐘,取到票後,他馬上騎腳踏車(勻速)趕往體育館。已知小明騎腳踏車從家趕往體育館比從體育館步行回家所用時間少20分鐘,騎腳踏車的速度是步行速度的3倍。
(1)小明步行的速度(單位:米/分鐘)是多少?
(2)小明能否在球賽開始前趕到體育館?
【解析】(1)設步行的速度為x米/分鐘,則騎腳踏車的速度為3x米/分鐘。
解得x=80,3x=240依題意得(2400╱x)-(2400╱3x)=20
經檢驗,x=80是原方程的根。
答:小明步行的速度是80米/分鐘。
(2)來回家取票總時間為:
(2400╱x)+(2400╱3x)+2=42分鐘<45分鐘
所以他能在球賽開始前趕到體育館。
答:小明能在球賽開始前趕到體育館。