向量值積分
黎曼-斯蒂爾傑斯型積分 常用的一種向量值積分。如果ƒ(t)是定義在[α,b]上,但取“值”於拓撲線性空間L的函式,則稱ƒ(t)是[α,b]上向量值函式。設ƒ(t)和g(t)分別是[α,b]上向量值和數值函式。任取【α,b】上分點組D: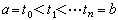 ,作和式
,作和式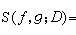
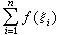
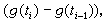 其中
其中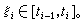 令
令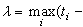
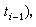 如果極限
如果極限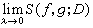 存在,則稱ƒ關於g在【α,b】上R-S可積,又稱
存在,則稱ƒ關於g在【α,b】上R-S可積,又稱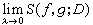 是ƒ關於g的黎曼-斯蒂爾傑斯積分,簡稱R-S積分,記為
是ƒ關於g的黎曼-斯蒂爾傑斯積分,簡稱R-S積分,記為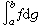 。類似地,也可以引入
。類似地,也可以引入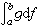 。向量值R-S積分有許多類似於數值函式的R-S積分的性質。特別,有分部積分公式:如果
。向量值R-S積分有許多類似於數值函式的R-S積分的性質。特別,有分部積分公式:如果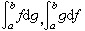 中有一個存在,則另一個必存在,且
中有一個存在,則另一個必存在,且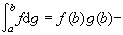
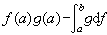 。
。 下面幾種向量值積分都屬於勒貝格型的。
博赫納積分 設(x,φ,μ)是全σ有限測度空間(見測度論),φ(x)是定義在x上,取值於巴拿赫空間B的向量值函式。如果存在 (x,φ)的有限個互不相交的可測集A1, A2, …,An,使φ在Ai(i=1,2,…,n)上的值恆為向量ei,而
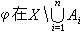 上的值恆為0,則稱φ是(向量值)簡單函式。如果存在 x上的一列簡單函式 {φn(x)},使得‖φn(x)-ƒ(x)‖關於μ幾乎處處收斂於0,則稱ƒ(x)是x上(取值於B)的強可測函式。強可測函式 ƒ(x)的範數‖ƒ(x)‖必是x上的(數值)可測函式。如果φ是簡單函式並且μ(Ai)<∞,那么稱
上的值恆為0,則稱φ是(向量值)簡單函式。如果存在 x上的一列簡單函式 {φn(x)},使得‖φn(x)-ƒ(x)‖關於μ幾乎處處收斂於0,則稱ƒ(x)是x上(取值於B)的強可測函式。強可測函式 ƒ(x)的範數‖ƒ(x)‖必是x上的(數值)可測函式。如果φ是簡單函式並且μ(Ai)<∞,那么稱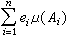 是φ的博赫納積分,記為
是φ的博赫納積分,記為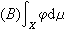 。設ƒ(x)是x上向量值函式,如果存在一個可積的簡單函式列{φn},使得
。設ƒ(x)是x上向量值函式,如果存在一個可積的簡單函式列{φn},使得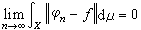 ,就稱ƒ是x上博赫納可積的,並稱
,就稱ƒ是x上博赫納可積的,並稱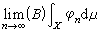 是ƒ在x上的博赫納積分,記為
是ƒ在x上的博赫納積分,記為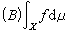 ,可以證明:對於博赫納可積函式ƒ,它的積分值(是向量)不依賴於{φn}的選取;ƒ在x上是博赫納可積的,若且唯若ƒ是強可測的而且‖ƒ(x)‖是 x上的數值可積函式。博赫納積分具有一般測度論中積分的性質。
,可以證明:對於博赫納可積函式ƒ,它的積分值(是向量)不依賴於{φn}的選取;ƒ在x上是博赫納可積的,若且唯若ƒ是強可測的而且‖ƒ(x)‖是 x上的數值可積函式。博赫納積分具有一般測度論中積分的性質。 伯克霍夫積分 設(x,φ,μ)是全σ有限測度空間,{Ai}是x的一列互不相交的可測集,
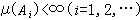 並且
並且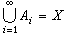 ,稱{Ai}是x的可列剖分。設ƒ(x)是x上取值於巴拿赫空間B的向量值函式,墹={Ai}是x的可列剖分,如果ƒ在每個Ai上有界,並且
,稱{Ai}是x的可列剖分。設ƒ(x)是x上取值於巴拿赫空間B的向量值函式,墹={Ai}是x的可列剖分,如果ƒ在每個Ai上有界,並且 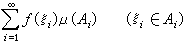
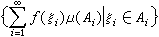 的凸閉包是ƒ(x)關於墹的積分值域,記為J(ƒ,墹)。如果對任何ε>0,存在可列剖分墹(ε),使集J(ƒ,墹(ε))的直徑小於ε,則稱ƒ在x上伯克霍夫可積,並稱由一切可列剖分墹所得的J(ƒ,墹)的交集(只有一個向量)為ƒ 在x上的伯克霍夫積分,記為
的凸閉包是ƒ(x)關於墹的積分值域,記為J(ƒ,墹)。如果對任何ε>0,存在可列剖分墹(ε),使集J(ƒ,墹(ε))的直徑小於ε,則稱ƒ在x上伯克霍夫可積,並稱由一切可列剖分墹所得的J(ƒ,墹)的交集(只有一個向量)為ƒ 在x上的伯克霍夫積分,記為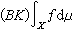 。這種積分除富比尼定理外,具有通常勒貝格積分所具有的線性、可列可加性、絕對連續性等性質。博赫納可積必然伯克霍夫可積(逆命題並不成立),並且兩個積分相等。
。這種積分除富比尼定理外,具有通常勒貝格積分所具有的線性、可列可加性、絕對連續性等性質。博赫納可積必然伯克霍夫可積(逆命題並不成立),並且兩個積分相等。 更一般地,還可定義取值於具有某種拓撲結構半群上的積分,當取不同拓撲時,它可包含伯克霍夫積分和下面的積分。
蓋爾范德意義下的弱*積分 設(x,φ,μ)是全σ有限測度空間,ƒ(x)是定義在x上取值於巴拿赫空間B的向量值函式。如果對每個g∈B*(B*是B的共軛空間),g(ƒ(x))是可測函式,則稱ƒ(x)在x上是弱可測的。在空間B是可分情況下,弱可測和強可測一致。如果對每個
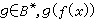 在x上是可積的,則必存在ƒ**∈B,使得
在x上是可積的,則必存在ƒ**∈B,使得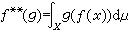 ,稱ƒ **是ƒ(x)在 X上的蓋爾范德意義下的弱*積分,記為
,稱ƒ **是ƒ(x)在 X上的蓋爾范德意義下的弱*積分,記為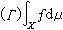 。
。 佩蒂斯積分 或稱弱積分。另一種常用的向量值積分。設(x,φ,μ)是全 σ有限測度空間,ƒ(x)是x上取值於巴拿赫空間B的弱可測函式,如果存在b)∈B 使得對一切g∈B*成立
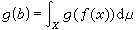 ,則稱ƒ在x上是佩蒂斯可積的,b)是ƒ的佩蒂斯積分,記b)為
,則稱ƒ在x上是佩蒂斯可積的,b)是ƒ的佩蒂斯積分,記b)為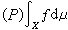 。博赫納可積必然佩蒂斯可積,並且積分相等。除去富比尼定理外,勒貝格積分的其他性質對於佩蒂斯積分也成立。
。博赫納可積必然佩蒂斯可積,並且積分相等。除去富比尼定理外,勒貝格積分的其他性質對於佩蒂斯積分也成立。 向量值測度和積分 設(x,φ)是可測空間,如果E是定義在φ上取值於巴拿赫空間 B的滿足下列條件的向量值集函式:①E(═)=0(═是空集);②可列可加性,對φ中任何一列互不相交的集{Ai},
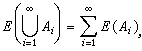
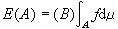 ,則E便是φ上取值於B的向量值測度。特別,當B是某個巴拿赫空間(或希爾伯特空間)上的有界線性運算元全體按運算元範數所成的巴拿赫空間時,就稱E為φ上的運算元值測度(見譜論、譜運算元)。此外,和數值測度一樣,也可引入一個向量值測度關於另一個數值測度絕對連續的概念。但一般說來沒有拉東-尼科迪姆定理。但如果空間B或是自反,或是希爾伯特空間,或B的共軛空間B*是可分的,這時就有拉東-尼科迪姆定理。(見測度論)
,則E便是φ上取值於B的向量值測度。特別,當B是某個巴拿赫空間(或希爾伯特空間)上的有界線性運算元全體按運算元範數所成的巴拿赫空間時,就稱E為φ上的運算元值測度(見譜論、譜運算元)。此外,和數值測度一樣,也可引入一個向量值測度關於另一個數值測度絕對連續的概念。但一般說來沒有拉東-尼科迪姆定理。但如果空間B或是自反,或是希爾伯特空間,或B的共軛空間B*是可分的,這時就有拉東-尼科迪姆定理。(見測度論)