正文
把非線性特性曲線分成若干個區段，在每個區段中用直線段近似地代替特性曲線，這種處理方式稱為分段線性化。在分段線性化處理後，所研究的非線性系統在每一個區段上被近似等效為線性系統，就可採用線性系統的理論和方法來進行分析。將各個區段的分析結果，如過渡過程曲線或相軌跡(見相平面法)，按時間的順序加以銜接，就是所研究非線性系統按分段線性化法分析得到的結果。
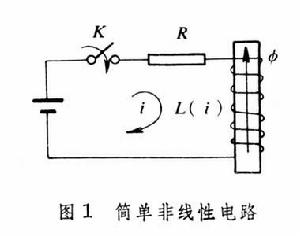
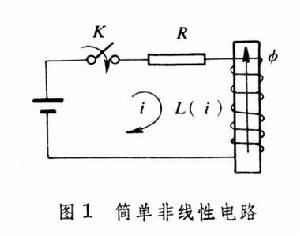
說明分段線性化法的原理和分析步驟的一個例子是簡單非線性電路系統。電路由電阻R和鐵芯線圈L串接組成，通過開關接入一個直流電壓源（圖1）。根據電路原理可知，描述這個電路在開關閉合後電流增長過程的運動方程是一個非線性微分方程：
分段線性化法
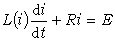
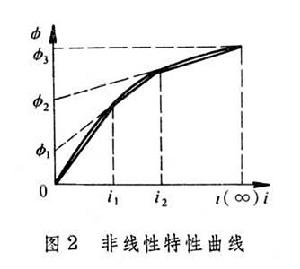
為，其中k為常數,磁通φ和電流i之間的關係具有圖2所示的非線性特性。電路的初始電流為i(0)=0，而在到達穩態時電路的穩態電流為I(∞)=E/R。在採用分段線性化法來分析時,先在電流值的有效區間【0,i(∞)】內，將非線性特性分成N（圖中N=3）個區段，且在每個區段內用直線近似代替曲線。在定出每個直線段和水平線的交角θ0、θ1、θ2後，可知相應於每個區段的等效線性電感值為L0=K0 tgθ0、L1=K1 tgθ1和L2=K2 tgθ2,其中K0、K1、K2為不同的常數。因此，在每一個區段,電路的運動方程都是線性的： 區段Ⅰ：
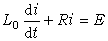0≤i＜i1 區段Ⅱ：
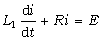i1≤i＜i2 區段Ⅲ：
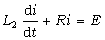i2≤i＜i(∞) 這些線性微分方程可用線性分析方法求解，其分析結果為
區段Ⅰ：
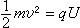
區段Ⅱ：
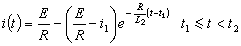
區段Ⅲ：
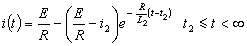
式中時間t1和t2的值可由區段Ⅰ和Ⅱ的電流表達式定出：
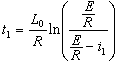和 
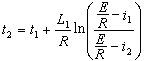
分段線性化法分段線性化法的分析精度和計算複雜性取決於系統非線性程度的高低。對於具有折線形狀的非線性特性，如繼電型非線性和死區非線性（見描述函式法），分段線性化法不會引入分析誤差，且計算上也不會增加複雜性。對於非線性程度較低的系統，分段線性化法具有比較好的分析結果。對於非線性程度高的系統，原則上分段線性化法仍可適用，但計算複雜性增加，而分析準確度則取決於線性化的區段數的多少。
