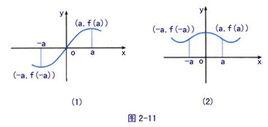
定義
設函式Y=f(u)的定義域為D，函式u=φ(x)的值域為Z，如果D∩Z，則y通過u構成x的函式，稱為x的複合函式，記作Y=f[φ(x)]。x為自變數，y為因變數，而u稱為中間變數。
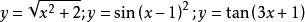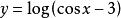複合函式如等都是複合函式。
複合函式而就不是複合函式，因為任何x都不能使y有意義。由此可見，不是任何兩個函式放在一起都能構成一個複合函式。
複合函式通俗地說就是函式套函式，是把幾個簡單的函式複合為一個較為複雜的函式。複合函式中不一定只含有兩個函式，有時可能有兩個以上，如y=f(u)，u=φ(v)，v=ψ(x)，則函式y=f{φ[ψ(x)]}是x的複合函式，u、v都是中間變數。
定義域
若函式 y= f( u)的定義域是B, u= g( x)的定義域是A,則複合函式 y= f[ g( x)]的定義域是D={ x| x∈A,且 g( x)∈B} 綜合考慮各部分的x的取值範圍，取他們的交集。
求函式的定義域主要應考慮以下幾點：
⑴當為整式或奇次根式時，R的值域；
⑵當為偶次根式時，被開方數不小於0（即≥0）；
⑶當為分式時，分母不為0；當分母是偶次根式時，被開方數大於0；
⑷當為指數式時，對零指數冪或負整數指數冪，底不為0（如，中）。
⑸當是由一些基本函式通過四則運算結合而成的，它的定義域應是使各部分都有意義的自變數的值組成的集合，即求各部分定義域集合的交集。
⑹分段函式的定義域是各段上自變數的取值集合的並集。
⑺由實際問題建立的函式，除了要考慮使解析式有意義外，還要考慮實際意義對自變數的要求
⑻對於含參數字母的函式，求定義域時一般要對字母的取值情況進行分類討論，並要注意函式的定義域為非空集合。
⑼對數函式的真數必須大於零，底數大於零且不等於1。
⑽三角函式中的切割函式要注意對角變數的限制。
周期性
設y=f(u)的最小正周期為T,μ=φ(x)的最小正周期為T,則y=f(μ)的最小正周期為T*T，任一周期可表示為k*T*T(k屬於R).
單調（增減）性
決定因素
依y=f(u)，μ=φ(x)的單調性來決定。即“增+增=增；減+減=增；增+減=減；減+增=減”，可以簡化為“ 同增異減”。
基本步驟
判斷複合函式的單調性的步驟如下：
⑴求複合函式的定義域；
⑵將複合函式分解為若干個常見函式（一次、二次、冪、指、對函式）；
⑶判斷每個常見函式的單調性；
⑷將中間變數的取值範圍轉化為自變數的取值範圍；
⑸求出複合函式的單調性。
例題
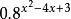複合函式例如：討論函式y= 的單調性。
解：函式定義域為R；
令u=x -4x+3,y=0.8 ；
指數函式y=0.8 在（-∞，+∞）上是減函式；
u=x -4x+3在（-∞,2]上是減函式，在[2,+∞）上是增函式；
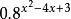複合函式∴ 函式y= 在（-∞,2]上是增函式，在[2,+∞）上是減函式。
複合函式求導
規則
複合函式求導的前提：複合函式本身及所含函式都可導。
法則1：設u=g(x)，對f(u)求導得：f'(x)=f'(u)*g'(x)；
法則2：設u=g(x),a=p(u)，對f(a)求導得：f'(x)=f'(a)*p'(u)*g'(x)；
複合函式的導數套用舉例
1、求：函式f(x)=(3x+2) +3的導數。
解：設u=g(x)=3x+2；
f(u)=u +3；
f'(u)=3u =3(3x+2) ；
g'(x)=3；
f'(x)=f'(u)*g'(x)=3(3x+2) *3=9(3x+2) ；
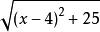複合函式2、求f(x)= 的導數。
解：設u=g(x)=x-4,a=p(u)=u +25
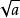複合函式f(a)= ；
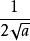複合函式
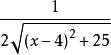複合函式f'(a)= = ；
p'(u)=2u=2(x-4)；
g'(x)=1；
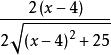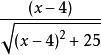複合函式
複合函式f'(x)=f'(a)*p'(u)*g'(x)= = .
