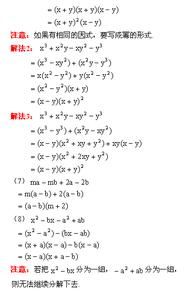概念闡述
概念定義
 因式分解
因式分解因式分解是中學數學中最重要的恆等變形之一,它被廣泛地套用於初等數學之中,在數學求根作圖、解一元二次方程方面也有很廣泛的套用,是解決許多數學問題的有力工具。
因式分解方法靈活,技巧性強。學習這些方法與技巧,不僅是掌握因式分解內容所必需的,而且對於培養解題技能、發展思維能力都有著十分獨特的作用。學習它,既可以複習整式的四則運算,又為學習分式打好基礎;學好它,既可以培養學生的觀察、思維發展性、運算能力,又可以提高綜合分析和解決問題的能力。
相關結論
基本結論:分解因式與整式乘法為相反。
高級結論:在高等數學上因式分解有一些重要結論,在初等數學層面上證明很困難,但是理解很容易。
1)因式分解與解高次方程有密切的關係。對於一元一次方程和一元二次方程,國中已有相對固定和容易的方法。在數學上可以證明,對於一元三次方程和一元四次方程,也有固定的公式可以求解。只是因為公式過於複雜,在非專業領域沒有介紹。對於分解因式,三次多項式和四次多項式也有固定的分解方法,只是比較複雜。對於五次以上的一般多項式,已經證明不能找到固定的因式分解法,五次以上的一元方程也沒有固定解法。
2)所有的三次和三次以上的一元多項式在實數範圍內都可以因式分解,所有的二次或二次以上的一元多項式在複數範圍內都可以因式分解。這看起來或許有點不可思議。比如x4+1,這是一個一元四次多項式,看起來似乎不能因式分解。但是它的次數高於3,所以一定可以因式分解。也可以用待定係數法將其分解,只是分解出來的式子並不整潔。(這是因為,由代數基本定理可知n次一元多項式總是有n個根,也就是說,n次一元多項式總是可以分解為n個一次因式的乘積。並且還有一條定理:實係數多項式的虛數根兩兩共軛的,將每對共軛的虛數根對應的一次因式相乘,可以得到二次的實係數因式,從而這條結論也就成立了。)
3)因式分解雖然沒有固定方法,但是求兩個多項式的公因式卻有固定方法。因式分解很多時候就是用來提公因式的。尋找公因式可以用輾轉相除法來求得。標準的輾轉相除技能對於中學生來說難度頗高,但是中學有時候要處理的多項式次數並不太高,所以反覆利用多項式的除法也可以但比較笨,不過能有效地解決找公因式的問題。
4)因式分解是很困難的,國中所接觸的只是因式分解很簡單的一部分。
分解公式
平方差公式
(a+b)(a-b)=a²-b²
完全平方公式
(a+b)²=a²+2ab+b²
(a-b)²=a²-2ab+b²
十字相乘法公式
x²+(a+b)x+ab=(x+a)(x+b)
平方和立方差公式
a³-b³=(a-b)(a²+ab+b²)
a³+b³=(a+b)(a²-ab+b²)
(a+b)³=a³+3a²b+3ab²+b³
(a-b)³=a³-3a²b+3ab²-b³
其他平方公式
a²+b²=(a+b)²-2ab
或=(a-b)²+2ab
a³+b³=(a+b)³-3ab(a+b)
a²+b²+c²=(a+b+c)²-2(ab+bc+ac)
a³+b³+c³-3abc=(a+b+c)(a²+b²+c²-ab-bc-ac)
解題方法
十字相乘法,待定係數法,雙十字相乘法,對稱多項式,輪換對稱多項式法,餘式定理法,求根公因式分解沒有普遍適用 的方法,國中數學教材中主要介紹了提公因式法、運用公式法、分組分解法。而在競賽上,又有拆項和添減項法式法,換元法,長除法,短除法,除法等。
注意四原則:
1.分解要徹底(是否有公因式,是否可用公式)
2.最後結果只有小括弧
3.最後結果中多項式首項係數為正(例如:-3x2+x=x(-3x+1))不一定首項一定為正,如-2x-3xy-4xz=-x(2+3y+4z)
歸納方法:
1.提公因式法。
2.運用公式法。
3.拼湊法。
提取公因式法
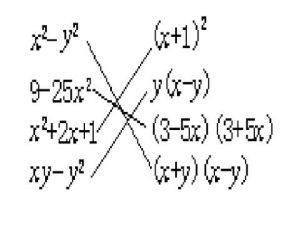 因式分解
因式分解各項都含有的公共的因式叫做這個多項式各項的公因式,公因式可以是單項式,也可以是多項式。
如果一個多項式的各項有公因式,可以把這個公因式提出來,從而將多項式化成兩個因式乘積的形式,這種分解因式的方法叫做提取公因式。
具體方法:當各項係數都是整數時,公因式的係數應取各項係數的最大公約數字母取各項的相同的字母,而且各字母的指數取次數最低的。當各項的係數有分數時,公因式係數為各分數的最大公約數。如果多項式的第一項是負的,一般要提出“-”號,使括弧內的第一項的係數成為正數。提出“-”號時,多項式的各項都要變號。
口訣:找準公因式,一次要提盡,全家都搬走,留1把家守,提負要變號,變形看奇偶。
例如:-am+bm+cm=-(a-b-c)m
a(x-y)+b(y-x)=a(x-y)-b(x-y)=(a-b)(x-y)。
注意:把變成不叫提公因式
公式法
如果把乘法公式的等號兩邊互換位置,就可以得到用於分解因式的公式,用來把某些具有特殊形式的多項式分解因式,這種分解因式的方法叫做公式法。
分解公式:
1、平方差公式: 即兩個數的平方差,等於這兩個數的和與這兩個數的差的積。
2、完全平方公式: 、即兩個數的平方和加上(或減去)這兩個數的積的2倍,等於這兩個數的和(或差)的平方。
注意:能運用完全平方公式分解因式的多項式必須是三項式,其中有兩項能寫成兩個數(或式)的平方和的形式,另一項是這兩個數(或式)的積的2倍。
口訣:首平方,尾平方,積的二倍放中央。同號加、異號減,符號添在異號前。
(1) 即三數和的平方,等於這三個數的平方和加上每兩項的積的2倍。
(2) 即四數和的平方,等於這四個數的平方和加上每兩數的積的2倍。即幾個數的和的平方,等於這幾個數的平方和加上每兩數的積的2倍。
3、立方和公式:
即兩數之和,乘它們的平方和與它們的積的差,等於這兩個數的立方和。
推廣:三項立方和公式
即三數之和,乘它們的平方和與它們兩兩的積的差,等於這三個數的立方和減三數之積的三倍。
4、立方差公式:
即兩數之差,乘它們的平方和與它們的積的和,等於這兩個數的立方差。
5、完全立方公式:
即兩數之和(差)的立方等於這兩個數的立方和(差)與每一個數的平方乘以另一個數3倍的和(和與差)。
6、兩根式:
例:a2+4ab+4b2=(a+2b)2
解方程法
通過解方程來進行因式分解,如:
X2+2X+1=0,解,得X1=-1,X2=-1,就得到原式=(X+1)×(X+1)
十字相乘法
對於x2+px+q型的式子如果q能分解為分解為數a,b的積,且有a + b = p時(即a與b和是一次項的係數),那么x2+(a+b)x+ab=(x+a)(x+b);或對於kx2+mx+n型的式子如果有k=ab,n=cd,且有ad+bc=m時,那么kx2+mx+n=(ax+c)(bx+d)。這種分解因式的方法叫做十字相乘法。
註:與十字相乘法對應的還有雙十字相乘法
具體方法:十字左邊相乘等於二次項係數,右邊相乘等於常數項,交叉相乘再相加等於一次項。
口訣:分二次項,分常數項,交叉相乘求和得一次項。(拆兩頭,湊中間)
特點:
(1)二次項係數是1;
(2)常數項是兩個數的乘積;
(3)一次項係數是常數項的兩因數的和。
基本步驟:
(1)把二次項係數和常數項分別分解因數;
(2)嘗試十字圖,使經過十字交叉線相乘後所得的數的和為一次項係數;
(3)確定合適的十字圖並寫出因式分解的結果;
(4)檢驗。
例1:把6x2 +13x + 6分解因式
解: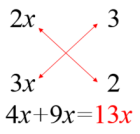
∴原式=(2x+3)(3x+2)
例2:把3m3 -3m2 -60m分解因式
解: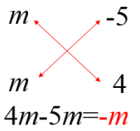
∴原式=3m(m2-m-20)=3m(m-5Xm+4)
雙十字相乘法
雙十字相乘法屬於因式分解的一類,類似於十字相乘法。
雙十字相乘法就是二元二次六項式,啟始的式子如下:
ax2+bxy+cy2+dx+ey+f
x、y為未知數,其餘都是常數
用一道例題來說明如何使用。
例:分解因式:x2+5xy+6y2+8x+18y+12.
分析:這是一個二次六項式,可考慮使用雙十字相乘法進行因式分解。
解:圖如下,把所有的數字交叉相連即可
x2y 2
x3y 6
∴原式=(x+2y+2)(x+3y+6).
雙十字相乘法其步驟為:
①先用十字相乘法分解2次項,如十字相乘圖①中x2+5xy+6y2=(x+2y)(x+3y)
②先依一個字母(如y)的一次係數分數常數項。如十字相乘圖②中6y2+18y+12=(2y+2)(3y+6)
③再按另一個字母(如x)的一次係數進行檢驗,如十字相乘圖③,這一步不能省,否則容易出錯。
④縱向相乘,橫向相加。
分組分解法
分組分解是分解因式的一種簡潔的方法,下面是這個方法的詳細講解。能分組分解的多項式有四項或大於四項,一般的分組分解有兩種形式:二二分法,三一分法。
比如:
ax+ay+bx+by
=a(x+y)+b(x+y)
=(a+b)(x+y)
我們把ax和ay分一組,bx和by分一組,利用乘法分配律,兩兩相配,立即解除了困難。
同樣,這道題也可以這樣做。
ax+ay+bx+by
=x(a+b)+y(a+b)
=(a+b)(x+y)
幾道例題:
1. 5ax+5bx+3ay+3by
解法:=5x(a+b)+3y(a+b)=(5x+3y)(a+b)
說明:係數不一樣一樣可以做分組分解,和上面一樣,把5ax和5bx看成整體,把3ay和3by看成一個整體,利用乘法分配律輕鬆解出。
2. x2-x-y2-y
解法:=(x2-y2)-(x+y)
=(x+y)(x-y)-(x+y)
=(x+y)(x-y-1)
利用二二分法,再利用公式法a2-b2=(a+b)(a-b),然後相合解決。
三一分法,例:a^2-b^2-2bc-c^2
=a^2-(b+c)^2
=(a-b-c)(a+b+c)
拆添項法
這種方法指把多項式的某一項拆開或填補上互為相反數的兩項(或幾項),使原式適合於提公因式法、運用公式法或分組分解法進行分解。要注意,必須在與原多項式相等的原則下進行變形。
例如:bc(b+c)+ca(c-a)-ab(a+b)
=bc(c-a+a+b)+ca(c-a)-ab(a+b)
=bc(c-a)+bc(a+b)+ca(c-a)-ab(a+b)
=bc(c-a)+ca(c-a)+bc(a+b)-ab(a+b)
=(bc+ca)(c-a)+(bc-ab)(a+b)
=c(c-a)(b+a)+b(a+b)(c-a)
=(c+b)(c-a)(a+b).
配方法
對於某些不能利用公式法的多項式,可以將其配成一個完全平方式,然後再利用平方差公式,就能將其因式分解,這種方法叫配方法。屬於拆項、補項法的一種特殊情況。也要注意必須在與原多項式相等的原則下進行變形。
例如:x2+3x-40
=x2+3x+2.25-42.25
=(x+1.5)2-(6.5)2
=(x+8)(x-5)
換元法
有時在分解因式時,可以選擇多項式中的相同的部分換成另一個未知數,然後進行因式分解,最後再轉換回來,這種方法叫做換元法。注意:換元後勿忘還元。
例如在分解(x2+x+1)(x2+x+2)-12時,可以令y=x2+x,則
原式=(y+1)(y+2)-12
=y2+3y+2-12=y2+3y-10
=(y+5)(y-2)
=(x2+x+5)(x2+x-2)
=(x2+x+5)(x+2)(x-1)
綜合除法
令多項式f(x)=0,求出其根為x1,x2,x3,……,xn,則該多項式可分解為f(x)=a(x-x1)(x-x2)(x-x3)……(x-xn).
例如在分解2x4+7x3-2x2-13x+6時,令2x4+7x3-2x2-13x+6=0,
則通過綜合除法可知,該方程的根為0.5,-3,-2,1.
所以2x4+7x3-2x2-13x+6=(2x-1)(x+3)(x+2)(x-1).
令y=f(x),做出函式y=f(x)的圖象,找到函式圖像與X軸的交點x1,x2,x3,……xn,則多項式可因式分解為f(x)=f(x)=a(x-x1)(x-x2)(x-x3)……(x-xn).
與方法⑼相比,能避開解方程的繁瑣,但是不夠準確。
主元法
例如在分解x3+2x2-5x-6時,可以令y=x3+2x2-5x-6.
作出其圖像,與x軸交點為-3,-1,2
則x3+2x2-5x-6=(x+1)(x+3)(x-2)
先選定一個字母為主元,然後把各項按這個字母次數從高到低排列,再進行因式分解。
特殊值法
將2或10代入x,求出數p,將數p分解質因數,將質因數適當的組合,並將組合後的每一個因數寫成2或10的和與差的形式,將2或10還原成x,即得因式分解式。
例如在分解x3+9x2+23x+15時,令x=2,則
x3+9x2+23x+15=8+36+46+15=105,
將105分解成3個質因數的積,即105=3×5×7.
注意到多項式中最高項的係數為1,而3、5、7分別為x+1,x+3,x+5,在x=2時的值,
則x3+9x2+23x+15可能等於(x+1)(x+3)(x+5),驗證後的確如此。
待定係數法
首先判斷出分解因式的形式,然後設出相應整式的字母係數,求出字母係數,從而把多項式因式分解。
例如在分解x4-x3-5x2-6x-4時,由分析可知:這個多項式沒有一次因式,因而只能分解為兩個二次因式。
於是設x4-x3-5x2-6x-4=(x2+ax+b)(x2+cx+d)
=x4+(a+c)x3+(ac+b+d)x2+(ad+bc)x+bd
由此可得
a+c=-1,
ac+b+d=-5,
ad+bc=-6,
bd=-4.
解得a=1,b=1,c=-2,d=-4.
則x4-x3-5x2-6x-4=(x2+x+1)(x2-2x-4).
因式定理
對於多項式f(x),如果f(a)=0,那么f(x)必含有因式x-a.
例如:f(x)=x2+5x+6,f(-2)=0,則可確定x+2是x2+5x+6的一個因式。(事實上,x2+5x+6=(x+2)(x+3).)
注意:1、對於係數全部是整數的多項式,若X=q/p(p,q為互質整數時)該多項式值為零,則q為常數項約數,p最高次項係數約數
2.對於多項式f(a)=0,b為最高次項係數,c為常數項,則有a為c/b約數
二次多項式
(根與係數關係二次多項式因式分解)
例:對於二次多項式aX2+bX+c(a≠0)
當△=b2-4ac≥0時,設aX2+bX+c=0的解為X1,X2
=a(X2-(X1+X2)X+X1X2)
=a(X-X1)(X-X2).
實際套用
1.套用於多項式除法。
:a(b−1)(ab+2b+a)
說明:(ab+b)2−(a+b)2=(ab+b+a+b)(ab+b−a−b)=(ab+2b+a)(ab−a)=a(b−1)(ab+2b+a).
2.套用於高次方程的求根。
3.套用於分式的通分與約分
順帶一提,梅森合數分解已經取得一些微不足道的進展:
1,p=4r+3,如果8r+7也是素數,則:(8r+7)|(2P-1)。即(2p+1)|(2P-1)
例如:
23|(211-1);;11=4×2+3
47|(223-1);;23=4×5+3
167|(283-1);,,,.83=4×20+3
2,p=2n×32+1,,則(6p+1)|(2P-1),
例如:223|(237-1);37=2×2×3×3+1
439|(273-1);73=2×2×2×3×3+1
3463|(2577-1);577=2×2×2×2×2×2×3×3+1
3,p=2n×3m×5s-1,則(8p+1)|(2P-1)
例如;233|(229-1);29=2×3×5-1
1433|(2179-1);179=2×2×3×3×5-1
1913|(2239-1);239=2×2×2×2×3×5-1
注意事項
因式分解中的四個注意,可用四句話概括如下:首項有負常提負,各項有“公”先提“公”,某項提出莫漏1,括弧裡面分到“底”。現舉下例可供參考例1把-a²-b²+2ab+4分解因式。解:-a²-b²+2ab+4=-(a²-2ab+b²-4)=-[(a-b)²-4]=-(a-b+2)(a-b-2)這裡的“負”,指“負號”。如果多項式的第一項是負的,一般要提出負號,使括弧內第一項係數是正的。防止學生出現諸如-9x²+4y²=(-3x)²-(2y)²=(-3x+2y)(-3x-2y)=(3x-2y)(3x+2y)的錯誤
例2把-12x2nyn+18xn+2yn+1-6xnyn-1分解因式。解:-12x2nyn+18xn+2yn+1-6xnyn-1=-6xnyn-1(2xny-3x2y2+1)
這裡的“公”指“公因式”。如果多項式的各項含有公因式,那么先提取這個公因式,再進一步分解因式;這裡的“1”,是指多項式的某個整項是公因式時,先提出這個公因式後,括弧內切勿漏掉1。
分解因式,必須進行到每一個多項式因式都不能再分解為止。即分解到底,不能半途而廢的意思。其中包含提公因式要一次性提“乾淨”,不留“尾巴”,並使每一個括弧內的多項式都不能再分解。防止學生出現諸如4x4y2-5x2y2-9y2=2y(4x4-5x2-9)=2y(2x+1)(4x2-9)的錯誤。
在沒有說明化到實數時,一般只化到有理數就夠了,有說明實數的話,一般就要化到實數!
由此看來,因式分解中的四個注意貫穿於因式分解的四種基本方法之中,與因式分解的四個步驟或說一般思考順序的四句話:“先看有無公因式,再看能否套公式,十字相乘試一試,分組分解要合適”等是一脈相承的。