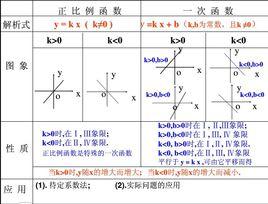
頂點式
二次函式有多條頂點式
對於任意一條頂點在坐標軸原點上的二次函式,有y=ax²
對於函式y=ax²,在X軸上平移h個單位,有y=a(x-h)²
對於函式y=ax²,在Y軸上平移k個單位,有y=ax²+k
對於函式y=a(x-h)²在Y軸上平移k個單位,或函式y=ax²+k在X軸上平移h個單位有:
y=a(x-h)²+k
y=a(x-h)²+k也是最常用的一條頂點式,通過代入特殊的點坐標,均可以轉換成y=ax²+k、y=a(x-h)²、y=ax²三者之一。
三角函式
 函式性質
函式性質三角函式是數學中屬於初等函式中的超越函式的一類函式。它們的本質是任意角的集合與一個比值的集合的變數之間的映射。通常的三角函式是在平面直角坐標系中定義的,其定義域為整個實數域。另一種定義是在直角三角形中,但並不完全。現代數學把它們描述成無窮數列的極限和微分方程的解,將其定義擴展到複數系。
由於三角函式的周期性,它並不具有單值函式意義上的反函式。
三角函式在複數中有較為重要的套用。在物理學中,三角函式也是常用的工具。
函式名 正弦 餘弦 正切 餘切 正割 餘割
符號 sin cos tan cot sec csc
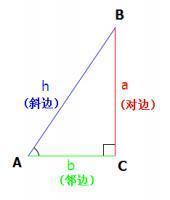
對邊(a) 臨邊(b) 斜邊(h)
正弦函式 sin(A)=a/h
餘弦函式 cos(A)=b/h
正切函式 tan(A)=a/b
餘切函式 cot(A)=b/a
正割函式 sec (A) =h/b
餘割函式 csc (A) =h/a
同角三角函式間的基本關係式
·平方關係:
sin^2(α)+cos^2(α)=1
tan^2(α)+1=sec^2(α)
cot^2(α)+1=csc^2(α)
·商的關係:
tanα=sinα/cosα cotα=cosα/sinα
·倒數關係:
tanα·cotα=1
sinα·cscα=1
cosα·secα=1
三角函式恆等變形公式
·兩角和與差的三角函式:
cos(α+β)=cosα·cosβ-sinα·sinβ
cos(α-β)=cosα·cosβ+sinα·sinβ
sin(α±β)=sinα·cosβ±cosα·sinβ
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
·倍角公式:
sin(2α)=2sinα·cosα
cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)
tan(2α)=2tanα/[1-tan^2(α)]
·三倍角公式:
sin3α=3sinα-4sin^3(α)
cos3α=4cos^3(α)-3cosα
·半角公式:
sin^2(α/2)=(1-cosα)/2
cos^2(α/2)=(1+cosα)/2
tan^2(α/2)=(1-cosα)/(1+cosα)
tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα
·萬能公式:
sinα=2tan(α/2)/[1+tan^2(α/2)]
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]
tanα=2tan(α/2)/[1-tan^2(α/2)]
·積化和差公式:
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]
·和差化積公式:
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
本章教學目標
1.(1)任意角的概念以及弧度制.正確表示象限角、區間角、終邊相同的角,熟練地進行角度制與弧度制的換算.
(2)任意角的三角函式定義,三角函式的符號變化規律,三角函式線的意義.
2.(1)同角三角函式的基本關係和誘導公式.
(2)已知三角函式值求角.
3.函式y=sinx、y=cosx、y=tanx以及y=Asin(ωx+φ)的圖像和“五點法”作圖、圖像法變換,理解A、ω、φ的物理意義.
4.三角函式的定義域、值域、奇偶性、單調性、周期性.
5.兩角和與差的三角函式、倍角公式,能正確地運用三角公式進行簡單的三角函式式的化簡、求值和恆等證明.
本章包括任意角的三角函式、兩角和與差的三角函式、三角函式的圖像和性質三部分.
三角函式是中學數學的重要內容,它是解決生產、科研實際問題的工具,又是進一步學習其他相關知識和高等數學的基礎,它在物理學、天文學、測量學以及其他各種套用技術學科中有著廣泛的套用.
函式的幾種特性
①有界性
 單調函式
單調函式②單調性③奇偶性
④周期性
公式一:
設α為任意角,終邊相同的角的同一三角函式的值相等:
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα
公式二:
設α為任意角,π+α的三角函式值與α的三角函式值之間的關係:
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
公式三:
任意角α與 -α的三角函式值之間的關係:
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
公式四:
利用公式二和公式三可以得到π-α與α的三角函式值之間的關係:
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
公式五:
利用公式一和公式三可以得到2π-α與α的三角函式值之間的關係:
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
公式六:
π/2±α及3π/2±α與α的三角函式值之間的關係:
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
(以上k∈Z)
最值問題
一次函式的最大值與最小值
一次函式y=kx+b在其定義域(全體實數)內是沒有最大值和最小值的,但是,如果對自變數x的取值範圍有所限制時,一次函式就可能有最大值和最小值了.
例1 設a是大於零的常數,且a≠1,求y的最大值與最小值.
大值a.
例2 已知x,y,z是非負實數,且滿足條件
x+y+z=30,3x+y-z=50.
求u=5x+4y+2z的最大值和最小值.
分析 題設條件給出兩個方程,三個未知數x,y,z,當然,x,y,z的具體數值是不能求出的.但是,我們固定其中一個,不妨固定x,那么y,z都可以用x來表示,於是u便是x的函式了.
解 從已知條件可解得
y=40-2x,z=x-10.
所以
u=5x+4y+2z
=5x+4(40-2x)+2(x-10)
=-x+140.
又y,z均為非負實數,所以
解得10≤x≤20.
由於函式u=-x+140是隨著x的增加而減小的,所以當x=10時,u有最大值130;當x=20時,u有最小值120.
二次函式的最大值與最小值
例3 已知x1,x2是方程
x-(k-2)x+(k+3k+5)=0
解 由於△=[-(k-2)]^2-4(k+3k+5)≥0,,所以二次方程有實根
3k+16k+16≤0,
例4 已知函式
有最大值-3,求實數a的值.
解 因為
的範圍內分三種情況討論.
-a+4a-1=-3
例5 已知邊長為4的正方形截去一個角後成為五邊形ABCDE(如圖3-12),其中AF=2,BF=1.試在AB上求一點P,使矩形PNDM有最大面積.
解 設矩形PNDM的邊DN=x,NP=y,於是矩形PNDM的面積
S=xy,2≤X≤4.
易知CN=4-x,EM=4-y,且有
二次函式S=f(x)的圖像開口向下,對稱軸為x=5,故當x≤5時,函式值是隨x的增加而增加,所以,對滿足2≤x≤4的S來說,當x=4時有最大值
例6 設p>0,x=p時,二次函式f(x)有最大值5,二次函式g(x)的最小值為-2,且g(p)=25,f(x)+g(x)=x+16x+13.求g(x)的解析式和p的值.
解 由題設知
f(p)=5,g(p)=25,
f(p)+g(p)=p+16p+13,
所以 p+16p+13=30,
p=1(p=-17捨去).
由於f(x)在x=1時有最大值5,故設
f(x)=a(x-1)+5,a<0,
所以
g(x)=x+16x+13-f(x)
=(1-a)x+2(a+8)x+8-a.
由於g(x)的最小值是-2,於是
解得a=-2,從而
g(x)=3x+12x+10.
分式函式的最大值與最小值
法是去分母后,化為關於x的二次方程,然後用判別式△≥0,得出y的取值範圍,進而定出y的最大值和最小值.
解 去分母、整理得
(2y-1)x+2(y+1)x+(y+3)=0.
△≥0,即
△=[2(y+1)]-4(2y-1)(y+3)≥0,
解得 -4≤y≤1.
時,取最小值-4,當x=-2時,y取最大值1.
說明 本題求最值的方法叫作判別法,這也是一種常用的方法.但在用判別法求最值時,應特別注意這個最值能否取到,即是否有與最值相應的x值.
解 將原函式去分母,並整理得
yx-ax+(y-b)=0.
因x是實數,故
△=(-a)-4·y·(y-b)≥0,
由題設知,y的最大值為4,最小值為-1,所以
(y+1)(y-4)≤0,
即 y-3y-4≤0. ②
由①,②得
所以a=±4,b=3.
其他函式的最大值與最小值
處理一般函式的最大值與最小值,我們常常用不等式來估計上界或下界,進而構造例子來說明能取到這個上界或下界.
解 先估計y的下界.
又當x=1時,y=1,所以,y的最小值為1.
說明 在求最小(大)值,估計了下(上)界後,一定要舉例說明這個界是能取到的,才能說這就是最小(大)值,否則就不一定對了.例如,本題我們也可以這樣估計:
但無論x取什麼值時,y取不到-3,即-3不能作為y的最小值.
例10 設x,y是實數,求u=x+xy+y-x-2y的最小值.
分析 先將u看作是x的二次函式(把y看作常數),進行配方後,再把餘下的關於y的代數式寫成y的二次函式,再配方後,便可估計出下界來.
又當x=0,y=1時,u=-1,所以,u的最小值為-1.
例11 求函式
的最大值,並求此時的x值,其中[a]表示不超過a的最大整數.
學習指導
函式的概念
(1)映射:設非空數集A,B,若對集合A中任一元素a,在集合B中有唯一元素b與之對應,則稱從A到B的對應為映射,記為f:A→B,f表示對應法則,b=f(a)。
(2)函式定義:函式就是定義在非空數集A,B上的映射,此時稱數集A為定義域,象集C=f(x)x∈A為值域。定義域,對應法則,值域構成了函式的三要素。
函式的通性
(1)奇偶性:函式定義域關於原點對稱是判斷函式奇偶性的必要條件,在利用定義判斷時,應在化簡解析式後進行,同時靈活運用定義域的變形,如f(-x)f(x)=0, (f(x)≠0)。
奇偶性的幾何意義是兩種特殊的圖像對稱。
(2)單調性:研究函式的單調性應結合函式單調區間,單調區間應是定義域的子集。
判斷函式單調性的方法:①定義法,即比差法;②圖像法;③單調性的運算性質(實質上是不等式性質);④複合函式單調性判斷法則。
(3)周期性:周期性主要運用在三角函式及抽象函式中,是化歸思想的重要手段。
求周期的重要方法:①定義法;②公式法;③圖像法;④利用重要結論:若函式f(x)滿足f(a-x)=f(a+x),f(b-x)=f(b+x),a≠b,則T=2b-2a。
(4)反函式:(考綱中反函式的教學,只要求通過比較同底的指數函式和對數函式,說明指數函式y=ax和對數函式y=loga x互為反函式(a > 0,a≠1)。)
函式的圖像
函式的圖像既是 函式性質的一個重要方面,又能直觀地反映函式的性質,在解題過程中,充分發揮圖像的工具作用。
圖像作法:①描點法;②圖像變換。應掌握常見的圖像變換。
本單元常見的初等函式:一次函式,二次函式,反比例函式,指數函式,對數函式。在具體的對應法則下理解函式的通性,掌握這些具體對應法則的性質。分段函式是重要的函式模型。
對於抽象函式,通常是抓住函式特性是定義域上恆等式,利用賦值法(變數代換法)解題。主要思想方法:數形結合,分類討論,函式方程,化歸等。