平面內到一個定點與一條定直線的距離之比是一個大於1的常數的動點的軌跡是雙曲線，這個常數即該雙曲線的離心率，定點是雙曲線的焦點，定直線是雙曲線的準線。
雙曲線上各點到焦點的距離比上到準線的距離為離心率e
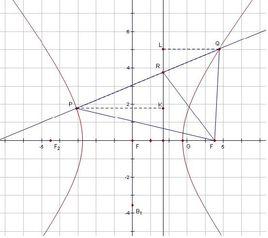
雙曲線有兩條準線 L（左準線）， L（右準線），準線與雙曲線的位置關係如右圖所示。
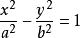雙曲線準線以原點為中心的雙曲線 的準線的方程就是：x=±a²/c；
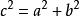雙曲線準線其中 a是實半軸長， b是虛半軸長， c是半焦距。（ ）
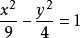雙曲線準線例如，存在以原點為中心的雙曲線 按照以上計算公式，則其準線方程為：
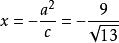雙曲線準線
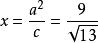雙曲線準線L的方程： ； L的方程： 。
雙曲線上任意一點P與雙曲線焦點的連線段，叫做雙曲線的焦半徑。
設雙曲線的焦點在x軸上。
設F1,F2為雙曲線的左右焦點，x為P的橫坐標，則
P在左支上時： PF1=-( a+ex） PF2=-（ ex-a)。
P在右支上時： PF1=a+ex, PF2=ex- a.
0)的點的軌跡，叫圓錐曲線。而這條定直線就叫做準線（Directrix）。0
圓錐曲線的準線方程 錐面上的準線0 a為長半軸 b為短半軸 c為焦距的一半)（亦可定義成：當動點P到定點F（焦點）和到定直線X=Xo的距離之比為離心率時，該直線便是橢圓的準線。）
準線的定義 準線的性質漸近線定義為如果曲線上的一點沿著趨於無窮遠時，該點與某條直線的距離趨於零，則稱此條直線為曲線的漸近線。雙曲線漸近線方程，是一種幾何圖形的算法，這種主要解...
基本公式 幾何性質 標準方程 注意事項 本節學習要求一般的，雙曲線（希臘語“ὑπερβολή”，字面意思是“超過”或“超出”）是定義為平面交截直角圓錐面的兩半的一類圓錐曲線。它還可以定義為與兩個固定的點（...
名稱定義 特徵介紹 實際套用 光學性質雙曲線漸近線方程，是一種幾何圖形的算法，這種主要解決實際中建築物在建築的時候的一些數據的處理。雙曲線的主要特點：無限接近，但不可以相交。分為鉛直漸近線、...
漸近線特點 幾何性質 注意、拋物線的切線與焦半徑的性質(準線作法) 4．橢圓、雙曲線、拋物線...、雙曲線、拋物線的相交焦點弦與準線關係 15．橢圓、雙曲線、拋物線的相交焦點弦與準線關係(角平分線) 16．橢圓、雙曲線、拋物線...
的不同，也包含了橢圓、雙曲線、拋物線以及各種退化情形。焦點--準線觀點...兩個“焦點－準線”的組合可以得到它。因此，橢圓和雙曲線有兩個焦點和兩條準線...時d為無窮遠線），則d為準線。圖只畫了橢圓，證明對拋物線雙曲線都適用，即...
歷史 定義 概念 定理 性質與錐面的兩條母線平行，所截曲線為雙曲線。 焦點與準線 如果圓錐曲線...截而得的曲線。當截面不通過錐面的頂點時，曲線可能是圓、橢圓、雙曲線...稱為圓錐曲線的準線。為了得到焦點與準線，只需作一個球面內切於圓錐面並同時...
二次曲線 正文 配圖 相關連線