基本內容
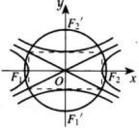
共軛雙曲線以已知雙曲線的虛軸為實軸,實軸為虛軸的雙曲線叫做原雙曲線的共軛雙曲線,通常稱它們互為共軛雙曲線.
共軛雙曲線有共同的漸近線;
共軛雙曲線的四個焦點共圓.
例 過雙曲線的一個頂點的切線交共軛雙曲線於兩點,求證:過交點所作共軛雙曲線的兩切線必通過原雙曲線的另一頂點.
點A′.
方程:x2/a2-y2/b2=1與y2/b2-x2/a2=1互為共軛雙曲線
雙曲線與橢圓有哪些不同?
(1)定義不同,圖形不同。
(2)有兩類特殊的雙曲線,它們有一些特殊的性質。
一類是等軸雙曲線。其主要性質有:a=b,離心率為根號2,兩條漸近線互相垂直,等軸雙曲線上任意一點到中心的距離是它到兩個焦點的距離的比例中項。
另一類是共軛雙曲線,其主要性質有:它們有共同的漸近線,它們的四個焦點共圓,它們的離心率的倒數的平方和等於1。
等軸雙曲線是一個方程所對應的幾何圖形。有兩支曲線:而互為共軛雙曲線則是兩個方程所對應的幾何圖形,每個方程各對應兩支曲線。等軸雙曲線也有它的共軛雙曲線。