ROC曲線的主要作用
1.ROC曲線能很容易地查出任意界限值時的對疾病的識別能力。
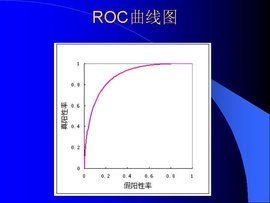
2.選擇最佳的診斷界限值。ROC曲線越靠近左上角,試驗的準確性就越高。最靠近左上角的ROC曲線的點是錯誤最少的最好閾值,其假陽性和假陰性的總數最少。
3.兩種或兩種以上不同診斷試驗對疾病識別能力的比較。在對同一種疾病的兩種或兩種以上診斷方法進行比較時,可將各試驗的ROC曲線繪製到同一坐標中,以直觀地鑑別優劣,靠近左上角的ROC曲線所代表的受試者工作最準確。亦可通過分別計算各個試驗的ROC曲線下的面積(AUC)進行比較,哪一種試驗的 AUC最大,則哪一種試驗的診斷價值最佳。
ROC曲線分析的主要步驟
1.ROC曲線繪製。依據專業知識,對疾病組和參照組測定結果進行分析,確定測定值的上下限、組距以及截斷點(cut-off point),按選擇的組距間隔列出累積頻數分布表,分別計算出所有截斷點的敏感性、特異性和假陽性率(1-特異性)。以敏感性為縱坐標代表 真陽性率,(1-特異性)為橫坐標代表 假陽性率,作圖繪成ROC曲線。
2.ROC曲線評價統計量計算。ROC曲線下的面積值在1.0和0.5之間。在AUC>0.5的情況下,AUC越接近於1,說明診斷效果越好。AUC在 0.5~0.7時有較低準確性,AUC在0.7~0.9時有一定準確性,AUC在0.9以上時有較高準確性。AUC=0.5時,說明診斷方法完全不起作用,無診斷價值。AUC<0.5不符合真實情況,在實際中極少出現。
3.兩種診斷方法的統計學比較。兩種診斷方法的比較時,根據不同的試驗設計可採用以下兩種方法:①當兩種診斷方法分別在不同受試者身上進行時,採用成組比較法。②如果兩種診斷方法在同一受試者身上進行時,採用配對比較法。
ROC曲線的意義
ROC曲線指受試者工作特徵曲線(receiver operating characteristic curve), 是反映敏感性和特異性連續變數的綜合指標,是用構圖法揭示敏感性和特異性的相互關係,它通過將連續變數設定出多個不同的臨界值,從而計算出一系列敏感性和特異性,再以敏感性為縱坐標、(1-特異性)為橫坐標繪製成曲線,曲線下面積越大,診斷準確性越高。在ROC曲線上,最靠近坐標圖左上方的點為敏感性和特異性均較高的臨界值。
ROC曲線的繪製
ROC曲線的具體繪製實例: 楊治良(1983)曾做過這樣一個實驗:選圖畫頁500頁,分成五個組,每組100張。五組畫頁的先定機率分別是0.1、0.3、0.5、0.7和0.9。對於每一組畫頁,主試者使用一種信號的先定機率,然後按此先定機率呈現給被試者一定數量的畫頁,要求被試者把它們當做“信號”記住。例如,先定機率為0.1時,則當作“信號”的畫頁為10張;當做“ 噪音”的畫頁為90張。作為信號的畫頁呈現完畢之後,與此組作為噪音的畫頁混合,然後隨機地逐張呈現給被試。這時,每呈現一張畫頁,即要求被試判斷此畫頁是“信號”還是“噪音”,並要求被試把結果記錄在實驗紙上。根據五種先定機率得到的實驗結果,就可計算擊中機率和虛驚機率。最後,根據不同先定機率下的擊中機率和虛驚機率,就可在圖上確定各點的位置,把五點聯接起來就繪成一條 ROC曲線。
例子
考慮一個二分問題,即將實例分成正類(positive)或負類(negative)。對一個二分問題來說,會出現四種情況。如果一個實例是正類並且也被 預測成正類,即為真正類(True positive),如果實例是負類被預測成正類,稱之為假正類(False positive)。相應地,如果實例是負類被預測成負類,稱之為真負類(True negative),正類被預測成負類則為假負類(false negative)。
列聯表如下表所示,1代表正類,0代表負類。
| | | 預測 | | |
| | | 1 | 0 | 合計 |
| 實際 | 1 | True Positive(TP) | False Negative(FN) | Actual Positive(TP+FN) |
| | 0 | False Positive(FP) | True Negative(TN) | Actual Negative(FP+TN) |
| 合計 | | Predicted Positive(TP+FP) | Predicted Negative(FN+TN) | TP+FP+FN+TN |
從列聯表引入兩個新名詞。其一是真正類率(true positive rate ,TPR), 計算公式為TPR=TP/ (TP+ FN),刻畫的是分類器所識別出的 正實例占所有正實例的比例。另外一個是假正類率(false positive rate, FPR),計算公式為FPR= FP / (FP + TN),計算的是分類器錯認為正類的負實例占所有負實例的比例。還有一個真負類率(True Negative Rate,TNR),也稱為specificity,計算公式為TNR=TN/ (FP+ TN) = 1 - FPR。
在一個二分類模型中,對於所得到的連續結果,假設已確定一個閥值,比如說 0.6,大於這個值的實例劃歸為正類,小於這個值則劃到負類中。如果減小閥值,減到0.5,固然能識別出更多的正類,也就是提高了識別出的正例占所有正例的比例,即TPR,但同時也將更多的負實例當作了正實例,即提高了FPR。為了形象化這一變化,在此引入ROC。
Receiver Operating Characteristic,翻譯為"接受者操作特性曲線",夠拗口的。曲線由兩個變數1-specificity 和 Sensitivity繪製. 1-specificity=FPR,即假正類率。Sensitivity即是真正類率,TPR(True positive rate),反映了正類復蓋程度。這個組合以1-specificity對sensitivity,即是以代價(costs)對收益(benefits)。
下表是一個邏輯回歸得到的結果。將得到的實數值按大到小劃分成10個個數 相同的部分。
| Percentile | 實例數 | 正例數 | 1-特異度(%) | 敏感度(%) |
| 10 | 6180 | 4879 | 2.73 | 34.64 |
| 20 | 6180 | 2804 | 9.80 | 54.55 |
| 30 | 6180 | 2165 | 18.22 | 69.92 |
| 40 | 6180 | 1506 | 28.01 | 80.62 |
| 50 | 6180 | 987 | 38.90 | 87.62 |
| 60 | 6180 | 529 | 50.74 | 91.38 |
| 70 | 6180 | 365 | 62.93 | 93.97 |
| 80 | 6180 | 294 | 75.26 | 96.06 |
| 90 | 6180 | 297 | 87.59 | 98.17 |
| 100 | 6177 | 258 | 100.00 | 100.00 |
其正例數為此部分里實際的正類數。也就是說,將邏輯回歸得到的結 果按從大到小排列,倘若以前10%的數值作為閥值,即將前10%的實例都劃歸為正類,6180個。其中,正確的個數為4879個,占所有正類的 4879/14084*100%=34.64%,即敏感度;另外,有6180-4879=1301個負實例被錯劃為正類,占所有負類的1301 /47713*100%=2.73%,即1-特異度。以這兩組值分別作為x值和y值,在excel中作散點圖。得到ROC曲線如下
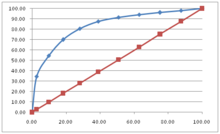 roc曲線
roc曲線ROC曲線的屬性
(1)β值的改變獨立於d’的變化,考察β值變化對P(y/SN)和P(y/N)的影響時發現:當β接近無窮大時,虛驚率幾乎為0,即噪音全當成信號接受;當β接近0時,擊中率幾乎為0,即信號全當成噪音接受;而當β從接近0向無窮大漸變的過程中,將形成一條完整地ROC曲線,曲線在某一處達到最佳的標準βOPT。
(2)ROC曲線的曲率反應敏感性指標d’:對角線,代表P(y/SN)=P(y/N),即被試者的辨別力d’為0,ROC曲線離這條線愈遠,表示被試者辨別力愈強,d’的值當然就愈大。由上可知,d’的變化使ROC曲線形成一個曲線簇,而β的變化體現在這一曲線簇中的某一條曲線上不同點的變化。此外,如果將ROC曲線的坐標軸變為Z分數坐標,我們將看到ROC曲線從曲線形態變為直線形態。這種坐標變換可以用來驗證 信號檢測論一個重要假設,即方差齊性假設。
SPSS軟體實現ROC分析
SPSS 9.0以上版本可進行ROC分析,操作步驟如下:
1.定義列變數,並輸入數據
(1)診斷分類值或檢測結果(test):多個診斷試驗則定義test1,test2,...
(2)金標準類別(group):1=病例組,0=對照組
(3)分類頻數(freq),需要進一步執行第二步
2.說明頻數變數 路徑:Data\Weight Case..., 選項:Weight case by, 填表:Freqency Variable (freq)
3.ROC分析:路徑:Grahps\Roc Curve... 填表:Test Variable(test), State Variable (group), Value of state variable,選項包括:
(display) ROC Curve,with diagonal reference line (機會線), standard error and confidence interval (面積的標準誤,及其可信區間), Coordinate points of the ROC curve (ROC曲線的坐標點), options:test direction (如果檢測值小劃歸為陽性,則需要選), cofidence level (%):需要除95%以外的可信度,可在此定義。
如果是連續型測量資料,則不需要第1步的(3)及第2步。
在R中繪製ROC曲線
ROCR包中主要是兩個class:prediction和performance。前者是將預測結果和真實標籤組合在一起,生成一個 prediction對象,然後在用performance函式,按照給定的評價方法,生成一個performance對象,最後直接對 performance用plot函式就能繪製出相應的ROC曲線。
| 1 2 3 4 5 6 | # plot a ROC curve for a single prediction run # and color the curve according to cutoff. data(ROCR.simple) pred <- prediction(ROCR.simple$predictions, ROCR.simple$labels) perf <- performance(pred,"tpr","fpr") plot(perf,colorize=TRUE) |
上面是ROCR中的一個例子,ROCR.simple$predictions是預測結果,ROCR.simple$labels是真實的標籤,從而產生一個prediction對象;然後tpr是true positive rate的意思,fpr則是false positive rate的意思,這樣最後畫出來的就是最常見的ROC曲線。
註:轉自擴展閱讀2的網址