定義
單調函式一般地，設函式的定義域為I：
單調函式如果對於屬於I內某個區間上的任意兩個自變數的值x1、x2，當x1>x2時都有f(x1)≥f(x2),那么就說在這個區間上是增函式(另一說法為單調不減函式)。
單調函式如果f(x1)>f(x2)，那么就說在這個區間上是嚴格增函式（另一種說法是增函式）。
如果對於屬於I內某個區間上的任意兩個自變數的值x1、x2，當x1>x2時都有f(x1)≤f(x2).那么就是f(x）在這個區間上是減函式(另一種說法為單調不增函式)。如果f(x1)<f(x2)，那么就說f(x）在這個區間上是嚴格減函式（另一種說法是減函式）。
為了迴避歧義，下文採取單調不減函式，嚴格增函式，單調不增函式，嚴格減函式等術語。
性質
基本性質
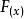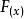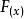單調函式 單調函式 單調函式如果函式y=在某個區間是增函式或減函式，就稱函式在這一區間具有（嚴格的）單調性，這一區間叫做y=的單調區間，在單調區間上增函式的函式圖像是上升的，減函式的函式圖像是下降的。
注意
•函式的單調性也叫函式的增減性；
•函式的單調性是對某個區間而言的，它是一個局部概念；
判定方法
判定函式在某個區間上的單調性的方法步驟有兩種主要方法：
定義法
設任意x1、x2∈給定區間，且x1
計算f(x1)- f(x2）至最簡。【最好表示為整式乘積的形式】
判斷上述差的符號。
1.設任意x1、x2∈給定區間，且x1
2.計算f(x1)- f(x2）至最簡。【最好表示為整式乘積的形式】
3.判斷上述差的符號。
求導法
利用導數公式進行求導，然後判斷導函式和0的大小關係，從而判斷增減性，導函式值大於0，說明是嚴格增函式，導函式值小於0，說明是嚴格減函式，前提是原函式必須是連續的。當導數大於等於0時也可為增函式，同理當導數小於等於0時也可為減函式。
推廣
現代數學中，在有序集合之間的函式是單調（monotone）的，如果它們保持給定的次序。這些函式最先出現在微積分中，後來推廣到序理論中更加抽象結構中。儘管概念一般是一致的，兩個學科已經發展出稍微不同的術語。在微積分中，我們經常說函式是單調遞增和單調遞減的，在序理論中偏好術語單調和反單調或序保持和序反轉。
在序理論中，不限制於實數集合，可以考慮任意偏序集合甚至是預序集合。在這些情況下上述定義同樣適用。但是要避免術語"遞增"和"遞減"，因為一旦處理的不是全序的次序就沒有了吸引人的圖像動機。進一步的，嚴格關係 < 和 > 在多數非全序的次序中很少使用，因此不介入它們的額外術語。
設f: P → Q為一函式映射，是在兩個帶有偏序的集合 P 和 Q 之間的函式映射。
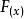單調函式
單調函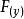式
單調函式如果x ≤ y 蘊涵≤，就稱為單調（monotone）函式，也叫做isotone 或序保持函式。
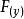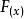單調函式 單調函式對偶概念經常叫做反單調、antitone 或序反轉。因此，反單調函式 f 滿足性質x ≤ y 蘊涵 ≥ ，
對於它的定義域中的所有 x 和 y。容易看出兩個單調函式的複合也是單調的。
常數函式是單調的也是反單調的；反過來，如果 f 是單調的也是反單調的，並且如果 f 的定義域是全序集，則 f 必定是常量函式。
單調函式是序理論的中心。它們大量出現於這個主題的文章和在這些地方的找到的套用中。
著名的特殊單調函式是序嵌入（x ≤ y若且唯若f(x) ≤ f(y) 的函式）和序同構（雙射序嵌入）。
