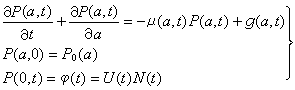結合代數
正文
一種代數系統,類似於群、環、域,而更接近於環。結合代數的研究,早在19世紀50年代,W.R.哈密頓考察四元數、H.G.格拉斯曼引入向量乘法以及A.凱萊等人討論矩陣代數之時就已開始,其目標是刻畫各種類型的結合代數的結構和表示。設A是非空集,F是域。在集A上定義有加法+和乘法·兩個運算,在F和A之間定義有數乘運算,即對於任意α∈F,α∈A有αα∈A,且滿足以下條件:①A關於加法+和乘法·作成結合環;②A關於加法+及數乘運算構成域F上的向量空間;③對任意α∈F,α、b∈A有α(αb)=(αα)b=α(αb),這種代數系統記作{A,+,·,數乘}並稱為域F 上結合代數,簡稱F上代數A或代數A。域F上向量空間A的維數也稱為F上代數A的維數。
環的加法群是一個交換群,而代數的加法群是域F上的向量空間,後者較前者的結構要簡單得多。例如,向量空間A必有基{αi,i∈I},而任意α∈A可惟一表成
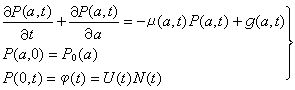 。於是只要知道αi之間的乘法表:
。於是只要知道αi之間的乘法表: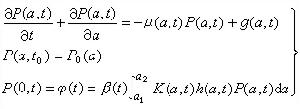 ,便可以計算A中任二元素
,便可以計算A中任二元素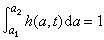 ,
,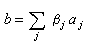 的乘積
的乘積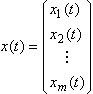
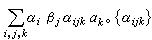 稱為代數A的構造常數。反之,通過規定向量空間A的一組基元之間的乘法,可線性擴張成A中的一個乘法。人們常利用這種方便定義新代數。
稱為代數A的構造常數。反之,通過規定向量空間A的一組基元之間的乘法,可線性擴張成A中的一個乘法。人們常利用這種方便定義新代數。 與環相類似,結合代數也有子代數、理想、同態、直積等概念。
例如,代數A的理想B,即指B是向量空間A的子空間,又是環A的理想。與除環和單環相應的概念,是可除代數和單代數等。
仿照由實數來構造複數的方法,可用複數來構造新的數。設Q是一切複數對(α,b)的集合,規定(α,b)=(с,d)若且唯若 α=с,b=d,並定義如下的運算:
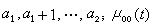
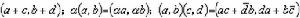 婔,廀是複數с,d的共軛數,α是實數。直接驗證可知,Q是實數域R上的一個四維結合代數,除了乘法交換律之外,Q的運算具有通常的數運算的所有性質。這是第一個非交換可除代數的例子。
婔,廀是複數с,d的共軛數,α是實數。直接驗證可知,Q是實數域R上的一個四維結合代數,除了乘法交換律之外,Q的運算具有通常的數運算的所有性質。這是第一個非交換可除代數的例子。 如令
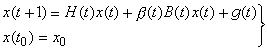 ,
, 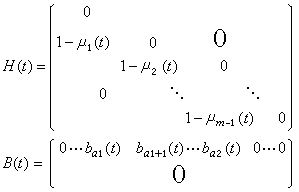 ,
, 則它們組成R上代數Q的一個基,而Q關於此基的乘法表是:1是單位元;
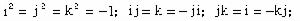
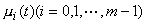 。這就是著名的四元數代數。
。這就是著名的四元數代數。 由於推廣數系而得出四元數代數,隨之產生出實數域與複數域上的結合代數的概念,最初曾稱之為:“超複數系”。實數域上有限維可除代數有三個而且只能有此三個:實數域、複數域、四元數代數。這就是著名的弗羅貝尼烏斯定理。而韋德伯恩定理則刻畫了關於有限域的情形:有限域上有限維可除代數只能是有限域。
域K上一切n×n矩陣的集合Kn關於矩陣的加法、乘法和數乘運算,作成一個n2維結合代數,而且是單代數。用域F上m維可除代數D去代替域K,就得到D上一切n×n矩陣組成的F上mn2維結合代數Dn。Dn也是單代數。
關於有限維結合代數的韋德伯恩理論,對代數的研究有深遠的影響。這一理論的主要內容是:①任意有限維結合代數A含有一個極大的冪零理想N(所謂N是冪零的,意指存在一個自然數n,使N中任意n個元素之積都是零),它包含A的一切冪零理想,N稱為A的冪零根,而商代數A/N的冪零根為零,冪零根為零的代數,稱為半單代數;②半單代數是有限個單代數的直和;③F上單代數必具有形式Dn,其中D是F上可除代數,且D和n是惟一的;④任意代數A=N+S(向量空間的直和),其中N是A的冪零根,S是A的半單代數。
Α.И.馬爾采夫證明了④中的子代數S在不計內自同構的意義下是惟一的。根據上述韋德伯恩定理,有限維代數的研究,基本上可歸結為對冪零代數與可除代數的研究。實際上這是研究代數的一個模式:對代數引入根的概念,從而可將對任意代數的研究化歸為對兩類特殊代數的研究。結合環的阿廷理論和雅各布森理論,以及關於非結合代數和環的一些研究都是按照這一模式進行的。
F上單代數A有單位元1,因此可認定F=F·1吇A。若A的中心(即與A中任意元素都是乘法可換的元素的全體)恰是F,則A稱為F上中心單代數。Fn是F上中心單代數。
張量積在研究單代數時起著重要作用。設A、B是F有單位元的代數。取A在F上的一個基:
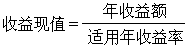 ,且
,且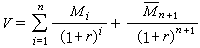
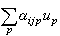 ;取B在F上的一個基:
;取B在F上的一個基: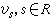 ,且
,且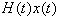 。以符號集
。以符號集 為基可作F上一個向量空間,記作A圱B。規定A圱B的一個乘法:
為基可作F上一個向量空間,記作A圱B。規定A圱B的一個乘法: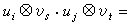
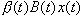
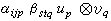 ,則得F上一個結合代數A圱B,稱之為F上代數A和B的張量積。可以證明,代數A圱B與A和B之基的選擇無關。兩個F上中心單代數的張量積仍是F上中心單代數。利用張量積可以定義張量代數,或者外代數、格拉斯曼代數(見多重線性代數)。
,則得F上一個結合代數A圱B,稱之為F上代數A和B的張量積。可以證明,代數A圱B與A和B之基的選擇無關。兩個F上中心單代數的張量積仍是F上中心單代數。利用張量積可以定義張量代數,或者外代數、格拉斯曼代數(見多重線性代數)。 令G表示F上有限維中心單代數的全體。在集合G中引入關係~:A~B若且唯若存在m、n∈Z +使得
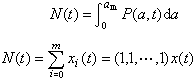
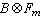 。容易證明,這是一個等價關係。令凴表示A所在的等價類,
。容易證明,這是一個等價關係。令凴表示A所在的等價類,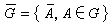 。在集合強中規定一個乘法:
。在集合強中規定一個乘法: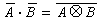 。可以證明,這個乘法定義是合理的,即與等價類凴的代表選擇無關,並且強關於此乘法作成一個群。稱群{強,·}為域F上的布饒爾群,記作B(F)。B(F)的結構反映了中心單代數間的張量積的性質。可以證明B(F)是交換周期群。
。可以證明,這個乘法定義是合理的,即與等價類凴的代表選擇無關,並且強關於此乘法作成一個群。稱群{強,·}為域F上的布饒爾群,記作B(F)。B(F)的結構反映了中心單代數間的張量積的性質。可以證明B(F)是交換周期群。 若A是F上n2維中心單代數,且含有一個子域K,而K是F上n次正規擴域,則A稱為一個交叉積。若K是域F上的循環擴域,則交叉積A特稱為循環代數。交叉積有比較簡單的乘法表,然而它有很好的代表性:B(F)中任一元素(即等價類凴中)必含有一個交叉積。
布饒爾-哈塞-諾特-阿爾貝特理論是有限維結合代數中特別重要而完美的理論。它闡明了有理數域上的每一個單代數(尤其可除代數)都是其中心F上的循環代數,也就是說,有理數域的有限擴域F上的中心單代數都是循環代數。近年來,S.阿米策等人討論了不是交叉積的可除代數。
所謂有限維結合代數的表示,是指代數到域F上矩陣代數Fn內的同態映射。有限維結合代數的表示理論與有限群表示論之間有密切的聯繫。設G是一有限群,其元素為g1,g2,…,gn,F是一域,作一個以g1,g2,…,gn為基元的n維向量空間,於是便得到F上一個結合代數,稱之為群代數,並記作F【G】。由結合代數F【G】的一個表示可得群G的一個表示。反之亦然。若域F的特徵不能整除群G的元素個數│G│,則F【G】是半單代數。這就是馬施克定理。由前述的韋德伯恩定理可進而得出半單代數的較為完整的表示理論,它可用來刻畫有限群的常表示。若為域F的特徵能整除│G│的情況,即有限群的模表示,則要求發展F上非半單代數的表示。弗羅貝尼烏斯代數、擬弗羅貝尼烏斯代數、單列代數以及它們的推廣,是首先研究的非半單代數類,在研究中廣泛使用了同調代數工具。近年來,代數的表示論在M.奧斯蘭德、P.加布里埃爾、A.V.羅伊特等人手中有很大發展,是很活躍的一個代數分支。
1933年中山正、松島與三證明了局部域上單代數的換位子群等於換 1元素群。王湘浩在1950年證明了上述二群在代數數域情形下仍相等,而且在一般域的情形下當指數無平方因子時也相等。這裡首先提出的在最一般的情形下的問題,這在以後興起的代數K理論和代數群理論中是很重要的。