李代數
正文
一類重要的非結合代數。最初是由19世紀挪威數學家M.S.李創立李群時引進的一個數學概念，經過一個世紀，特別是19世紀末和20世紀的前葉，由於W.基靈、É.(-J.)嘉當、（C.H.）H.外爾等人卓有成效的工作，李代數本身的理論才得到完善，並且有了很大的發展。無論就其理論的完整性還是就其套用的廣泛性來說，李代數都已成為一個非常重要的數學分支。它的理論和方法已經滲透到數學和理論物理的許多領域。定義 如果令F是一個域，集合g稱為F上的一個李代數是指:①g是F上一個向量空間。②g帶有一個二元運算，稱為換位運算,即對於任意X,Y∈g，有g中惟一確定的元素(記為【X,Y】)與之對應。③ 滿足下列三條件即對於任意α、b∈F,X,Y,Z∈g,有【αX+bY,Z】=α【X,Z】+b【Y，Z】，【X,αY+bZ】=α【X，Y】+ b【X，Z】；【X，X】=0；【【X,Y】,Z】+【【Y,Z】，X】+【【Z,X】,Y】=0（雅可比恆等式）。
李代數g作為F上向量空間,它的維數稱為李代數g的維數。
由③中的前兩個條件可推出，對於任意X，Y∈g，有【X,Y】=-【Y,X】；反之,當F的特徵不為2時可由此式推出③中的第二個條件。
設g是域F上一個向量空間,在g中定義換位運算：對於X,Y∈g，令【X,Y】=0，則g作成一個李代數，稱為交換（或阿貝爾）李代數。
在R3={(x1,x2,x3)｜xi∈R,R 是實數域，i=1, 2，3}中, 設
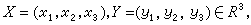
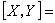
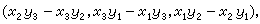則R3作成R上一個李代數。 令V 是域F上一個向量空間。可知V的一切線性變換作成F上一個向量空間，設ƒ、g是V的線性變換,令ƒg表示ƒ與g的合成,並定義【ƒ,g】=ƒg-gƒ，直接驗證可知，V的全體線性變換所組成的向量空間，對於這樣定義的換位運算,作成F上一個李代數。這個李代數稱為全線性李代數，記作g
(V)。 類似地,域F上全體n×n矩陣所組成的向量空間，對於換位運算【A,B】=AB-BA（A、B是n×n矩陣）,作成F上一個李代數，並稱之為F上全陣李代數，記作g
(n,F)。 更一般地,設U是域F上一個結合代數。對於α、b∈U定義【α,b】=αb-bα，則U作成F上一個李代數。
子代數、理想、商代數、同態 令g是域F上一個李代數，α、b是g的子空間。記【α,b】=｛Σ【A,B】(有限和)│A∈α,B∈b ｝，則【α, b】是g的一個子空間。設α是g的一個子空間。如果【α, α】嶅α，那么就稱α是g的一個子代數;如果【α, g】嶅α,那么α就稱為g的一個理想。由於【α,g】=【g,α】，因此李代數的理想都是雙邊的。如果α是g的一個理想，在商空間g/α里，定義【X+α,Y+α】=【X,Y】+α，那么g/α作成F上一個李代數,稱為g模α的商代數。
設g1、g2是域F上李代數。ƒ:g1→g2是一個線性映射。如果對於X、Y∈g,ƒ(【X,Y】)=【ƒ(X), ƒ(Y)】，那么ƒ就稱為一個同態映射。如果ƒ還是一個雙射，那么就稱ƒ是一個同構映射,這時g1與g2就稱為同構,記作g1≌g2。設ƒ:g1→g2是一個同態映射，則 Im ƒ=ƒ(g1)是g2的一個子代數,而Kerƒ＝ƒ-1(0)是g1的一個理想，並且ƒ導出一個同構g1/Ker ƒ≌Im ƒ。
設V是域F上一個n維向量空間。通過取定V的一個基，可以在全線性李代數g
（V）與全陣李代數 g(n, F)之間建立同構，因而常把這兩個李代數看成是一樣的。g(n,F)（或g(V)）的子代數稱為線性李代數。一些重要的線性李代數如下： t(n,F)={(αij)｜(αij)∈g(n,F)，αij=0,若i>j}。它是F上一切n×n上三角形矩陣所組成的集合。 n(n,F)={(αij)｜(αij)∈t(n,F),αij=0,1≤i≤n}，即主對角線上元素都是0的 n×n上三角形矩陣所組成的集合。 容易驗證,t(n,F)和n(n,F)都是g
(n,F)的子代數。 域F上一切跡是0(即主對角線上元素的和等於0)的n×n 矩陣,作成g
(n,F)的一個理想,記作s(n,F)。當F是複數域，而n=l+1(l≥1)時，這個李代數通常記作Al，稱為特殊線性李代數。 取定域F上一個n×n對稱或反對稱矩陣M。 令g={X∈g
(n,F)| tXM+MX =0}(tX表示X的轉置), 則g是g(n,F)的子代數。現設F是複數域，M是一個非退化對稱矩陣，於是M與以下兩個矩陣之一契約： 當n=2l+1，
；
。
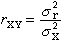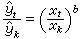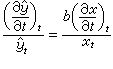
可解李代數、冪零李代數 設g是域F上一個李代數，α、b是g的理想，那么【α,b】仍是g的一個理想，特別,g(1)=【g,g】, g(2)=【g(1),g(1)】,…,gn+1=【g(n), g(n)】，…都是g的理想。於是有g叾g(1)叾g(2)叾…，稱為g的導出鏈。g(1)稱為g的導出代數。如果存在一個正整數n，使得g(n)={0}，那么就說g是可解的。
再定義g1=g,g2=【g,g1】,…,gn+1=【g,gn】,…，又可得到g的一個理想序列g1叾g2叾…,稱為g的降中心鏈。如果存在一個正整數n，使得gn={0}，那么就說g是冪零的。因為g(i)嶅gi，所以冪零李代數一定是可解的。
例如，線性李代數t(n,F)是可解的,而n(n,F)是冪零的，事實上,t(n,F)(n)={0},n(n,F)n={0}。這兩個例子具有普遍的意義，因為有以下兩個定理。
恩格爾定理 令V是域F上一個n（大於零）維向量空間，g是g
(V)的一個子代數。如果g的元素都是V的冪零線性變換, 那么存在V的一個非零向量v，使得對於每一個X∈g都有X·v=0，因此，適當選取V的基，並且將g(V)與g(n,F)看成一樣的,就有g嶅n(n,F)。 李定理 令F是一個特徵為0的代數閉域，V是F上一個n（大於零）維向量空間,g是g
(V)的一個可解子代數，則存在V 的一個非零向量v，使得對於每一X ∈g都有Xv＝φ(X)v，φ(X)∈F。因此適當選取V的基可以使得g嶅t(n，F)。 單李代數、半單李代數 域F上一個李代數g是所謂單的，即指除了g本身和{0}以外,g不含其他理想。F上一個有限維李代數g是所謂半單的，即指g不含非零可解理想。每一個有限維李代數g都含有惟一的最大可解理想r,就是這樣一個理想, 它包含g的一切可解理想，稱為g的根基。g是半單的若且唯若它的根基 r＝{0}。除一維李代數外,有限維單李代數都是半單的。特徵為0的域上每一個半單李代數都是一些單李代數的直和。
李代數的表示 令g是域F上一個李代數，V 是F上一個向量空間。李代數的一個同態ρ: g→g
(V)，稱為g在V上的一個線性表示,簡稱表示。用(ρ，V)代表g在V上的表示ρ，V稱為ρ的表示空間。當dimV=n時,取定V的一個基，將g(V)與g(n,F)看成一樣,於是就得到一個李代數同態ρ: g→g(n,F)，仍記作ρ,稱為g的一個矩陣表示。如果g的一個表示ρ是單射，那么就稱(ρ,V)是一個忠實表示。有阿多－岩沢定理：域F上每一個有限維李代數都有一個忠實表示。 設(ρ,V)是李代數g的一個表示。V的一個子空間W稱為ρ(g)不變的，即指W在一切ρ(X)(X∈g)之下不變。李代數g的一個表示(ρ,V)稱為不可約的，是指除{0}和V本身外,V沒有其他ρ(g)不變子空間。所謂(ρ,V)是完全可約的,意即V是一些ρ(g)不變的子空間的直和,並且ρ在每一個這樣的子空間上的限制都是不可約的。有外爾定理：特徵為 0的域上半單李代數的每一（有限維）表示都是完全可約的。
最重要的一種表示就是所謂伴隨表示。設X是李代數g的一個元素。對於每一Y∈g，定義adX(Y)=【X,Y】，則adX是g的一個線性變換,並且ad∶X→adX(X∈g)是g到g
(g)的一個同態映射(利用雅可比恆等式很容易驗證)。因此，(ad,g)是g的一個表示。表示空間就是g本身，稱為g的伴隨表示。 設(ρ，V)是g的一個有限維表示。定義一個對稱雙線性型 k:g×g→F；對於X、Y ∈g, 定義k(X,Y)=Trρ(X)·ρ(Y)(ρ(X)ρ(Y)的跡)。特別,當g是有限維的而ρ是伴隨表示ad時, k稱為g的基靈型。基靈型在研究李代數的結構中起重要的作用。例如有嘉當判定準則：特徵為0的域上一個(有限維)李代數是半單的,必要而且只要g的基靈型非退化。
復半單李代數的根系和分類 複數域(或一般地,特徵為0的代數閉域)上的半單李代數的結構和分類，早在19世紀末就已經得到。
令g是域F上一個李代數。g的一個子代數
稱為一個嘉當子代數，是指是冪零子代數，且與它在g內的正規化子
相重合。 設g是複數域上一個半單李代數，這時g的一個子代數
是嘉當子代數，必要而且只要是具有以下兩個性質的極大子代數：① 是交換的；② 對於的每一個元素h,adh是g上一個可對角化的線性變換。g一定有嘉當子代數，並且g的任意兩個嘉當子代數都可以通過g的一個內自同構將其中一個變成另一個。 取定g的一個嘉當子代數
。設dim=l，並稱為g的秩。令*是的對偶空間(即上一切線性函式所成的空間)。設 α∈*,令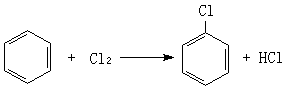
，對一切h ∈},則gα是g的子空間,並且g0={X∈g｜【h,X】=0，對一切h∈}=。如果α≠0且gα≠{0},那么就稱α是g關於的一個根，而α稱為屬於根α的根子空間。令墹表示g關於的根全體,稱為g關於的根系,那么g可以分解成子空間的直和:
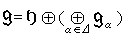，其中每一個根子空間 gα都是一維的。這種分解（在同構意義下）不依賴於的選取。 g的基靈型 k 在
上的限制是非退化的，因而對於*中每一元素λ,存在惟一的元素hλ∈,使得λ(h)=k(hλ, h)對於一切h∈成立。因而就有一個同構*→,使得 λ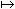
hλ。於是k在*上誘導出一個非退化對稱雙線性型
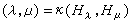,對一切λ、μ∈*。 令墹是g關於一個嘉當子代數
的根系。墹的一個子集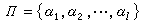
稱為墹的一個基礎系,是指墹的每一元素 α可以惟一地表成
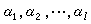的整係數線性組合：
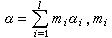是整數,並且要么都≥0,要么都≤0。墹的一個基礎系所含的根的個數等於g的秩l，因而作成的一個基。g是單的，若且唯若基礎系Ⅱ不能分解成兩個不相交的非空子集Ⅱ1與Ⅱ2的並集，並且對於任意α∈Ⅱ1和β∈Ⅱ2，都有(α,β)=0。 複數域上單李代數（在同構的意義下）由它們根的基礎系完全刻畫。有以下的結果:在同構的意義下,複數域上單李代數只有Al(l≥1)Bl（l≥1）、Cl（l≥1）、Dl(l≥3)這四類和五個例外李代數，分別記作G2、F4、E6、E7、E8、它們的維數分別是14、52、78、133和248。除了A1≌B1≌C1,B2≌C2,A3≌D3外,這些李代數互不同構。
復半單李代數的實型和謝瓦萊基 設g是複數域C上一個半單李代數。實數域R上一個李代數g0稱為g的一個實型,是指
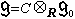，這時g稱為g0的復化。設g0是g的一個實型,於是g0總可以看成g的一個實子代數，並且
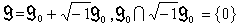。g的一個實型gu稱為緊的,是指g的基靈型在gu上的限制是負定的。一個復半單李代數g（在同構意義下）只有惟一的緊實型，然而可以有若干互不同構的非緊實型。一個實李代數g0是半單（或單）的,若且唯若它的復化是半單（或單）的。實單李代數的分類問題與不可約對稱黎曼空間的分類問題是密切相關的。這個問題也已完全解決。 在一個復半單李代數 g里， 總存在著這樣一個基{h1，h2,…,hl；Eα,α∈墹},這裡h1,h2,…，hl是一個嘉當子代數
的基，而墹是g關於的根系，Eα∈gα，α∈墹,具有以下性質:①α(hi),i=1，2,…,l，α∈墹都是整數；②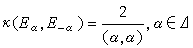
;③如果α、β及α+β都是根，那么 
,
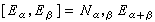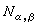是整數且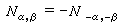
。這樣的一個基稱為g的一個謝瓦萊基。取定g的一個謝瓦萊基,於是
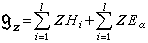是整數環Z上一個李代數。令
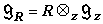,於是gR是g的一個實型而 
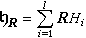是g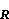
的一個嘉當子代數，並且adh(h∈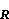)在 g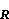上的特徵值都是實數。這樣一個實型稱為g的正規實型。一個復半單李代數g的正規實型是彼此共軛的(即在g的內自同構作用下是傳遞的)。 特徵為p>0的域上的李代數和卡茨－穆迪代數 令g是一個復單李代數。取定g的一個謝瓦萊基,可以作出gZ。設K是任意域,於是
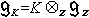就是K上一個李代數。當K是一個特徵為p>0的代數閉域時，通過這種途徑得到的gK記作
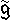。那么與復單李代數相對應,就得到K 上李代數 
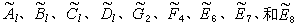。這些李代數，除了┯l在l+1呏0(modp)的情形外,也都是單的，然而和特徵為0的情形不同,這些李代數遠遠沒有窮盡特徵為p>0的代數閉域上的單李代數。K上另一類重要的李代數是所謂嘉當型李代數。這種李代數與É.嘉當的偽群中所產生的無限維單李代數極其類似。這種李代數分成四類，通常分別記為 Wn、Sn、hn和Kn，其中Wn是單的,而其他三類也很接近於單的。 1968年，V.卡茨和R.穆迪彼此獨立地提出了一類新的李代數，這種李代數可以看成復半單李代數在無限維的很自然的類比，稱之為卡茨－穆迪代數。
特徵為p>0的域上的李代數和卡茨-穆迪代數的研究正方興未艾，與其他學科的聯繫也很廣泛，許多問題有待解決。
參考書目
萬哲先編著：《李代數》，科學出版社，北京，1964。
嚴志達著：《半單純李群李代數表示論》，上海科學技術出版社，上海，1963。
N.賈柯勃遜著，曹錫華譯：《李代數》，上海科學技術出版社，上海，1964。(N.Jacobson,Lie Algebras,John Wiley & Sons.New York, 1962.)
N.Bourbaki,Eléments de Mathématique,GroupesetAlgébre de Lie,Actualités Sci. lnd., Hermann, 1960,1968.
V. Kac,lnfinite Dimensional Lie Algebras,Birkhuser, Basel-Stuttgart, 1983.
