簡介
由此推出,n次復係數多項式方程在複數域內有且只有n個根（重根按重數計算）。代數學基本定理說明，任何復係數一元 n次多項式方程在複數域上至少有一根(n≥1)。
有時這個定理表述為：任何一個非零的一元n次復係數多項式，都正好有n個複數根。這似乎是一個更強的命題，但實際上是“至少有一個根”的直接結果，因為不斷把多項式除以它的線性因子，即可從有一個根推出有n個根。
儘管這個定理被命名為“代數基本定理”，但它還沒有純粹的代數證明，許多數學家都相信這種證明不存在 。另外，它也不是最基本的代數定理；因為在那個時候，代數基本上就是關於解實係數或復係數多項式方程，所以才被命名為代數基本定理。
證明歷史
代數基本定理在代數乃至整個數學中起著基礎作用。 據說，關於代數學基本定理的證明，現有200多種證法。 迄今為止，該定理尚無純代數方法的證明。大數學家 J.P. 塞爾 曾經指出：代數基本定理的所有證明本質上都是拓撲的。 美國數學家John Willard Milnor在數學名著《從微分觀點看拓撲》一書中給了一個幾何直觀的證明，但是其中用到了和臨界點測度有關的sard定理。 複變函數論中，對代數基本定理的證明是相當優美的，其中用到了很多經典的複變函數的理論結果。
該定理的第一個證明是法國數學家達朗貝爾給出的，但證明不完整。接著，歐拉也給出了一個證明，但也有缺陷，拉格朗日於1772年又重新證明了該定理，後經高斯分析，證明仍然很不嚴格的。
代數基本定理的第一個嚴格證明通常認為是高斯給出的(1799年在哥廷根大學的博士論文)，基本思想如下：
代數基本定理設
為n次實係數多項式，記
，考慮方根：
代數基本定理
代數基本定理即
與
代數基本定理這裡
與
分別表示oxy坐標平面上的兩條曲線C1、C2，於是通過對曲線作定性的研究，他證明了這兩條曲線必有一個交點
，從而得出
，即
，因此z0便是方程
的一個根，這個論證具有高度的創造性，但從現代的標準看依然是不嚴格的，因為他依靠了曲線的圖形，證明它們必然相交，而這些圖形是比較複雜，正中隱含了很多需要驗證的拓撲結論等等。
高斯後來又給出了另外三個證法，其中第四個證法是他71歲公布的，並且在這個證明中他允許多項式的係數是複數。
證明方法
所有的證明都包含了一些數學分析，至少是實數或複數函式的連續性概念。有些證明也用到了可微函式，甚至是解析函式。
定理的某些證明僅僅證明了任何實係數多項式都有複數根。這足以推出定理的一般形式，這是因為，給定復係數多項式p(z)，以下的多項式
代數基本定理就是一個實係數多項式，如果z是q(z)的根，那么z或它的共軛複數就是p(z)的根。
代數基本定理許多非代數證明都用到了“增長引理”：當|z|足夠大時，首係數為1的n次多項式函式p(z)的表現如同z。一個更確切的表述是：存在某個正實數R，使得當|z| > R時，就有：
複分析證明
證明一
尋找一個中心為原點，半徑為r的閉圓盤D，使得當|z| ≥ r時，就有|p(z)| > |p(0)|。因此，|p(z)|在D內的最小值（一定存在，因為D是緊緻的），是在D的內部的某個點z0取得，但不能在邊界上取得。於是，根據最小模原理，p(z0) = 0。也就是說，z0是p(z)的一個零點（根）。
證明二
由於在D之外，有|p(z)| > |p(0)|，因此在整個複平面上，|p(z)|的最小值在z0取得。如果|p(z0)| > 0，那么1/p在整個複平面上是有界的全純函式，這是因為對於每一個複數z，都有|1/p(z)| ≤ |1/p(z0)|。利用劉維爾定理（有界的整函式一定是常數），可知1/p是常數，因此p是常數。於是得出矛盾，所以p(z0) = 0。
證明三
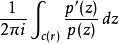代數基本定理這個證明用到了輻角原理。設R為足夠大的正實數，使得p(z)的每一個根的絕對值都小於R；這個數一定存在，因為n次多項式函式最多有n個根。對於每一個r > R，考慮以下的數：
其中c(r)是中心為0，半徑為r的逆時針方向的圓；於是輻角原理表明，這個數是p(z)在中心為0、半徑為r的開圓盤內的零點的數目N，由於r > R，所以它也是p(z)的零點的總數目。另一方面，n/z沿著c(r)的積分除以2πi，等於n。但這兩個數的差為：
代數基本定理被積分的有理表達式中的分子，次數最多是n 1，而分母的次數是n + 1。因此，當r趨於+∞時，以上的數趨於0。但這個數也等於N n，因此有N = n。
證明四
這個證明結合了線性代數和柯西積分定理。為了證明每一個n > 0次復係數多項式都有一個根，只需證明每一個方塊矩陣都有一個複數特徵值。證明用到了反證法。
設A為大小n > 0的方塊矩陣，並設In為相同大小的單位矩陣。假設A沒有特徵值。考慮預解函式
代數基本定理它在複平面上是亞純函式，它的值位於矩陣的向量空間內。A的特徵值正好是R(z)的極點。根據假設，A沒有特徵值，因此函式R(z)是整函式，根據柯西積分定理可知：
代數基本定理另一方面，把R(z)展開為幾何級數，可得：
代數基本定理這個公式在半徑為||A||的閉圓盤的外部（A的運算元範數）成立。設r > ||A||。那么：
代數基本定理（僅當k = 0時，積分才不等於零）。於是得出矛盾，因此A一定有一個特徵值。
拓撲學證明
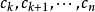代數基本定理設z0 ∈ C為使|p(z)|在z0取得最小值的數; 從用到劉維爾定理的證明中，可以看到這樣一個數一定存在。我們可以把p(z)寫成z z0的多項式：存在某個自然數k和一些複數
，使得
，以及：
代數基本定理
代數基本定理可推出如果a是
的一個k重根，且t是足夠小的正數，那么|p(z0 + ta)| < |p(z0)|，這是不可能的，因為|p(z0)|是|p|在D內的最小值。
代數基本定理對於另外一個用到反證法的拓撲學證明，假設p(z)沒有根。選擇一個足夠大的正數R，使得對於|z| = R，p(z)的第一項z大於所有其它的項的和；也就是說，|z| > |an 1z + ··· + a0|。當z依逆時針方向繞過方程為|z| = R的圓一次時，p(z)，像z那樣，依逆時針方向繞過零n次。在另外一個極端，|z| = 0時，“曲線” p(z)僅僅是一個（非零的）點p(0)，它的卷繞數顯然是0。如果z所經過的迴路在這兩個極端中被連續變形，那么p(z)的路徑也連續變形。我們可以把這個變形記為
，其中t大於或等於0，而小於或等於1。如果我們把變數t視為時間，那么在時間為零時，曲線為p(z)，時間為1時，曲線為p(0)。顯然在每一個點t，根據原先的假設p(z)都不能是零，因此在變形的過程中，曲線一直都沒有經過零。因此曲線關於0的繞數應該不變。然而，由於繞數在一開始是n，結束時是0，因此得出矛盾。所以，p(z)至少有一個根。
代數證明
代數基本定理這個證明需要依賴實數集的如下事實：正實數R在
上有實平方根，以及任何奇次多項式在
上有一個根（這可以用介值定理證明）。
代數基本定理首先
。經過簡單的計算可以證明
在開平方運算下是封閉的（利用事實1）。結合
。得出
不存在二階擴張。
代數基本定理由於
，於是任何
的擴張都是可分的，從而任何
的代數擴張都可以被包含在一個伽羅瓦擴張內。假設
是一個伽羅瓦擴張。考慮伽羅瓦群
的西羅2-子群H。那么
是奇數。由本原元定理得出，K存在本原元
，它的極小多項式是奇次的。但是利用實數集的事實2，任何奇次數多項式在實數上有一個根，於是不存在奇次的且次數>1的不可約多項式。於是
是2的冪次。
代數基本定理假設
並且r>0，再次利用西羅定理，G存在一個階為2的子群N。這時
。這和
先前不存在二階擴張矛盾。因此
的任何代數擴張都是本身，代數基本定理得證。
