公式
全排列數f(n)=n!(定義0!=1)
遞歸算法
1,2,3
1,3,2
2,1,3
2,3,1
3,2,1
3,1,2
這是由於算法只是考慮到了如何輸出全排列，而沒有考慮到換位是否有問題。所以我提出了解決方案，就是換位函式修改下
如 1 2 3 換位的話 ,不應該直接 3 2 1這樣 ,讓3和1直接換位; 而是讓3排在最前後 ,1 2 依次向後
基本算法
以下介紹全排列算法四種：
(A)字典序法
(B)遞增進位制數法
(C)遞減進位制數法
(D)鄰位對換法
字典序法
對給定的字元集中的字元規定了一個先後關係，在此基礎上規定兩個全排列的先後是從左到右逐個比較對應的字元的先後。 [例]字元集{1,2,3},較小的數字較先,這樣按字典序生成的全排列是:123,132,213,231,312,321。
[注意] 一個全排列可看做一個字元串，字元串可有前綴、後綴。
1）生成給定全排列的下一個排列 所謂一個的下一個就是這一個與下一個之間沒有其他的。這就要求這一個與下一個有儘可能長的共同前綴，也即變化限制在儘可能短的後綴上。
[例]839647521是1--9的排列。1—9的排列最前面的是123456789，最後面的是987654321，從右向左掃描若都是增的，就到了987654321，也就沒有下一個了。否則找出第一次出現下降的位置。
遞增進位制數
1)由排列求中介數 在字典序法中，中介數的各位是由排列數的位決定的.中介數位的下標與排列的位的下標一致。
在遞增進位制數法中，中介數的各位是由排列中的數字決定的。即中介數中各位的下標與排列中的數字(2—n)一致。可看出n-1位的進位鏈。 右端位逢2進1，右起第2位逢3進1，…， 右起第i位逢i+1進1，i=1,2,…,n-1. 這樣的中介數我們稱為遞增進位制數。 上面是由中介數求排列。
由序號（十進制數）求中介數（遞增進位制數）如下：
m=m1,0≤m≤n!-1
m1=2m2+kn-1,0≤kn-1≤1
m2=3m3+kn-2,0≤kn-2≤2
……………
mn-2=(n-1)mn-1+k2,0≤k2≤n-2
mn-1=k1,0≤k1≤n-1
p1p2…pn←→(k1k2…kn-1)↑←→m
在字典序法中由中介數求排列比較麻煩，我們可以通過另外定義遞增進位制數加以改進。
為方便起見，令ai+1=kn-1，i=1,2,…,n-1
(k1k2…kn-1)↑=(anan-1…a2)↑
ai：i的右邊比i小的數字的個數
在這樣的定義下，
有839647521←→(67342221)↑
(67342221)↑+1=(67342300)↑←→849617523
6×8+7)×7+3)×6+4)×5+2)×4+2)×3+2)×2+1 =279905
由(anan-1…a2)↑求p1p2…pn。
從大到小求出n,n-1,…,2,1的位置
_ ... _ n _ _ …_ (an個空格)
n的右邊有an個空格。
n-1的右邊有an-1個空格。
…………
2的右邊有a2個空格。
最後一個空格就是1的位置。
遞減進位制數
在遞增進位制數法中，中介數的最低位是逢2進1，進位頻繁，這是一個缺點。把遞增進位制數翻轉,就得到遞減進位制數。 (anan-1…a2)↑→(a2a3…an-1an)↓
839647521→ (12224376)↓
(12224376)↓=1×3+2)×4+2)×5+2)×6+4)×7+3)×8+7)×9+6=340989
[注意]求下一個排列十分容易
鄰位對換法
遞減進位制數法的中介數進位不頻繁，求下一個排列在不進位的情況下很容易。這就啟發我們，能不能設計一種算法，下一個排列總是上一個排列某相鄰兩位對換得到的。遞減進位制數字的換位是單向的，從右向左，而鄰位對換法的換位是雙向的。 這個算法可描述如下：
對1—n-1的每一個偶排列，n從右到左插入n個空檔(包括兩端)，生成1—n的n個排列。
對1—n-1的每一個奇排列，n從左到右插入n個空檔，生成1—n的n個排列。
對[2,n]的每個數字都是如此。
839647521
字典序法 遞增進位製法 遞減進位製法 鄰位對換法
下一個 839651247 849617523 893647521 836947521
中介數 72642321↑ 67342221↑ 12224376↓ 10121372↓
序 號 297191 279905 340989 203393
生成樹
生成樹中介數
可以採用樹的結構表示全排列生成算法，以數字的全排列生成算法為例，從最小的數1開始，其全排列只有一種可能；加入數字2，數字2可以插入在1的後邊或前邊，有兩個不同位置；再加入3，對於第二層中的每一種不同排列，都可以通過將3插入不同位置得到三種不同的排列數，共有6種排列數；一次類推可以得到個數的全排列。
基於此，可以構造一種新的中介數，其定義如下：
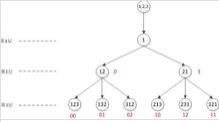
全排列生成樹與生成樹中介數示意圖對於生成樹中的第層，每一個節點中介數的前-2位繼承於其父節點的中介數，中介數最後一位為該層新加入的數減去其右邊相鄰的數。如果新加入的數在最右邊，則中介數最後一位為0。
如圖所示，排列數12的中介數為0，對於生成樹第三層由節點12擴展得到的新節點，當新加入的數3位於最右邊時（即排列數123），對應的中介數為00；若3插入12中間，則中介數末位為3-2=1，即中介數為01；類似地排列數312對應的中介數為02。
全排列生成樹與生成樹中介數示意圖不難看出，生成樹中介數也是遞減進位制數，但和遞減進位制數法是不同的。如排列數231對應的生成樹中介數為12，而遞減進位制數法對應的中介數為11。
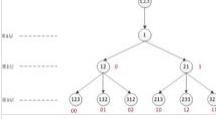全排列生成樹與生成樹中介數示意圖
全排列生成樹與生成樹中介數示意圖
全排列生成樹與生成樹中介數示意圖算法完備性
不難看出，全排列生成樹每一層的不同節點對應的中介數都是不同的，這是因為：
（1）每個子節點中介數的前綴都從其父節點繼承得到，因此不同父節點生成的子節點中介數一定不同；
（2）同一個父節點生成的子節點，父節點的排列數每一位都是不同的，因此新加入的數插入不同位置得到的中介數的最後一位一定是不同的。
由以上兩點及歸納法即可證明生成樹每一層不同節點對應的中介數都是唯一不重複的。又全排列生成樹每一個節點的排列數是無重複無遺漏的，因此從中介數到排列數的映射是一一對應的，從而基於生成樹中介數的全排列生成算法是完備的。
計算排列數
由生成樹中介數還原排列數的過程實際上就是全排列生成樹的構建過程。以生成樹中介數121為例：
（1）中介數第一位是1，說明2在1的左邊，得到21；
（2）中介數第二位為2，只能由3-1得到，說明3在1的左鄰，得到231；
（3）中介數第三位為1，只能由4-3得到，說明4在3的左鄰，得到2431.
對於任意的生成樹中介數，都通過類似的過程計算對應的排列數。不難看出，從生成樹中介數還原排列數的時間複雜度也是。
遞歸與非遞歸
遞歸(分治法思想)
設(ri)perm(X)表示每一個全排列前加上前綴ri得到的排列.當n=1時,perm(R)=(r) 其中r是唯一的元素,這個就是出口條件.
當n>1時,perm(R)由(r1)perm(R1),(r2)perm(R2),...(rn)perm(Rn)構成.
void Perm(list[],int k,int m) //k表示前綴的位置,m是要排列的數目.
{
if(k==m-1) //前綴是最後一個位置,此時列印排列數.
{
for(int i=0;i
{
printf("%d",list[i]);
}
printf("\n");
}
else
{
for(int i=k;i
{
//交換前綴,使之產生下一個前綴.
Swap(list[k],list[i]);
Perm(list,k+1,m);
//將前綴換回來,繼續做上一個的前綴排列.
Swap(list[k],list[i]);
}
}
}
//此處為引用,交換函式.函式調用多,故定義為內聯函式.
inline void Swap(int &a,int &b)
{
int temp=a;a=b;b=temp;
}
函式Perm(int list[],int k,int m)是求將list的第0~k-1個元素作為前綴、第k~m個元素進行全排列得到的全排列，如果k為0，且m為n，就可以求得一個數組中所有元素的全排列。其想法是將第k個元素與後面的每個元素進行交換，求出其全排列。這種算法比較節省空間。
非遞歸
n個數的排列可以從1.2....n開始,至n.n-1....2.1結束。
也就是按數值大小遞增的順序找出每一個排列。
以6個數的排列為例，其初始排列為123456,最後一個排列是654321,
如果當前排列是124653,找它的下一個排列的方法是，從這個序列中
從右至左找第一個左鄰小於右鄰的數，如果找不到，則所有排列求解
完成，如果找得到則說明排列未完成。本例中將找到46,計4所在的
位置為i,找到後不能直接將46位置互換，而又要從右到左到第一個
比4大的數，本例找到的數是5，其位置計為j，將i與j所在元素交換
125643,然後將i+1至最後一個元素從小到大排序得到125346，這
就是124653的下一個排列，如此下去，直至654321為止。算法結束。
int b[N];
int is_train(int a[],int n)
{
int i,j,k=1 ;
for(i=1;i<=n;i++)
{
for(j=i+1;j<=n;j++)
if(a[j]
/*判斷是否降序*/
if(k>1)is_train(b,k);
else return(1);
}
}
void train(int a[],int n)
{
int i,j,t,temp,count=1 ;
t=1 ;
printf("input the %3dth way:",count);
for(i=1;i<=n;i++)
printf("%3d",a[i]);
printf("\n");
while(t)
{
i=n ;
j=i-1 ;
/*從右往左找,找第一個左鄰比右鄰小的位置*/
while(j&&a[j]>a[i])
{
j--;
i--;
}
if(j==0)t=0 ;
else t=1 ;
if(t)
{
i=n ;
/*從右往左找,找第一個比front大的位置*/
while(a[j]>a[i])
i--;
temp=a[j],a[j]=a[i],a[i]=temp ;
quicksort(a,j+1,N);/*調用快速排序*/
/*判斷是否符合調度要求*/
if(is_train(a,N)==1)
{
count++;
printf("input the %3dth way:",count);
for(i=1;i<=n;i++)
printf("%3d",a[i]);
printf("n");
}
}
}
}
Pascal
program e;
var
n,t:longint;
a:array[1..8] of integer;
flag:array[1..8] of boolean;
procedure search(depth:integer); {depth變數表示正在搜尋第幾個元素}
var
i:integer;
begin
if(depth>n) then {depth>n表明已經搜尋到了第n個數，那么輸出結果}
begin
for i:=1 to n do write(a[i]:4);
writeln;
inc(t);
exit; {此種結果輸出後，退出該層搜尋}
end;
for i:=1 to n do {枚舉下一個出現的元素}
if flag[i]=false then {判斷是否已經出現過}
begin
a[depth]:=i; {沒有出現，則把第depth個數設為i}
flag[i]:=true; {給這個標誌變數給出出現的標誌}
search(depth+1); {遞歸搜尋下一個元素}
flag[i]:=false; {回溯，此時恢復這個標誌變數為沒出現的標誌}
end;
end;
begin
writeln('input N:');
read(n);
t:=0;
fillchar(flag,sizeof(flag),false); {賦初值，設定全部沒有出現過}
search(1);
writeln('Total=",t);
end.
VB
Option Explicit"修改:TZWSOHO
Private Sub Command1_Click()
Dim nt As Double: nt = Timer
List1.Visible = False: List1.Clear
Permutation "", Text1.Text
List1.Visible = True
Debug.Print Timer - nt,
End Sub
'遞歸求全排列'算法描述:
'以8位為例，求8位數的全排列，其實是8位中任取一位
'在後加上其餘7位的全排列
'7 位：任取一位，其後跟剩下6位的全排列
'……'這樣就有兩部分，一部分為前面的已經取出來的串，另一部分為後面即將進行的全排列的串
'參數pre即為前面已經取出來的串
'參數str即為將要進行排列的串
Private Sub Permutation(pre As String, s As String)
Dim i As Long
'// 如果要排列的串長度為1，則返回
If Len(s) = 1 Then List1.AddItem pre & s: Exit Sub
'// for循環即是取出待排列的串的任一位
For i = 1 To Len(s)
'// 遞歸，將取出的字元併入已經取出的串
'// 那么剩下的串即為待排列的串
Permutation pre & Mid$(s, i, 1), Left$(s, i - 1) & Mid$(s, i + 1)
Next
End Sub
字典序法
#include
int * array;
int num;
inline void xchg(int &a, int &b)
{
int c=a;
a=b;
b=c;
}
//從pos到num的數據進行翻轉
void invert(int pos)
{
int count=num-pos+1;
for(int i=0; i
xchg(array[pos+i],array[num-i]);
}
//檢查輸入中是否有重複數值
bool is_valid(int data, int serial)
{
for(int i=1; i
if(array[i]==data)
{
printf("全排列中不能有數據重複！\n");
return 0;
}
return 1;
}
//輸出全排列
void print_permutation(int m)
{
printf("之後第%d個全排列: ", m);
for(int i=1; i<=num; i++)
printf("%d ", array[i]);
printf("\n");
}
//字典序全排列的主體
void dictionary()
{
printf("輸入起始的全排列:\n");
for(int i=1; i<=num; i++)
{
int data;
scanf("%d", &data);
if(is_valid(data,i))
array[i]=data;
else
return;
}
if(num==1)
{
printf("只有一個數，不需進行排列！\n");
return;
}
int count;
printf("預測之後第幾個序列：\n");
scanf("%d", & count);
//一次循環找下一個全排列
for(int m=1; m<=count; m++)
{
int pos1=0;
int pos2;
//從num-1開始，找到第一個比右邊值小的位置
for(int j=num-1; j>0; j--)
if(array[j]
{
pos1=j;
break;
}
if(pos1<1 || pos1>num)
{
printf("目前全排列已為%d位數的最後一個全排列！\n\n",num);
return;
}
//從num開始找array[pos1]小的第一個數的位置
for(int n=num; n>pos1; n--)
if(array[n]>array[pos1])
{
pos2=n;
break;
}
xchg(array[pos1],array[pos2]);
//從pos1+1到num的數進行翻轉
invert(pos1+1);
print_permutation(m);
}
}
void main()
{
printf("輸入要進行全排列的位數\n");
scanf("%d", #);
array=new int[num+1];
while(1)
dictionary();
}
並行加速
由於全排列生成中包含大量規則一致的映射和運算操作，因而可以利用並行計算的方法對全排列的生成算法進行加速，這裡提出了一種基於GPU並行計算的加速框架，可以與現有全排列生成算法整合，以實現全排列生成的加速。具體而言，針對全排列算法本身支持的不同操作，有如下三種情況：
中介數映射
若全排列生成算法只支持中介數→排列的映射，那么我們可以提出如下的加速框架：
考慮全排列算法A，其支持的操作為：先按照一定規則R產生中介數I，接著基於某種映射算法根據每箇中介數I計算出其對應的全排列P。這樣，在遍歷了所有n!箇中介數後，便可以產生所有的全排列。
可以看出，其並行部分主要體現在從中介數I映射產生排列P的過程上，因而，可以採用如下的算法框架：
1、產生包含所有中介數的集合S
2、將S分割成為m個子集，其中m為GPU核數。
3、對於並行計算的每個核，其獨立計算每個子集Si中所有中介數→排列的映射。
4、合併所有核的計算結果。
可以看出，在理想的情況下，該算法框架的加速比應為m。
隨機遞推
一般而言，生成所有全排列時，遞推算法的效率要高於中介數→排列的映射。因而，對於支持遞推操作的全排列生成算法，可以提出更最佳化的框架。另一方面我們可以看到，某些全排列生成算法只支持遞推操作而不存在對應的中介數，所以，對於這類算法，我們的加速框架應如下修改：
考慮全排列算法A，其支持的操作為：先產生原始排列P0，接著基於某種遞推算法，根據當前得到的排列產生下一個排列，計算序列為P0→P1→P2……→Pn。這樣，在遍歷了所有n!個排列後，便可以產生所有的全排列。
可以看出，每個單獨的遞推過程是互不干擾的。因而，我們可以通過產生多個遞推的種子，通過多核同時遞推的方式來對遞推進行加速。但是，由於我們對算法的細節並沒有更多的認識，所以初始種子的產生並沒有可以依賴的規則。在實踐中，可以採用隨機的方法，隨機產生m個種子。其對應的算法框架如下：
1、隨機產生m個初始排列，其中m為GPU核數。
2、對於並行計算的每個核，其獨立根據初始排列中的一個進行遞推，直到其抵達了某個已經產生過的排列為止。
3、合併所有核的計算結果。
這裡需要注意的是，在該算法框架下，每個核的任務量很可能是不平均的。每次遞推產生一個新排列，都需要檢查是否已經出現過。若沒有出現過，則可以繼續遞推，否則意味著這個核的任務結束。在實踐中，可以通過一個長度為n!的bool數組來記錄每個排列的出現情況，通過hash算法來實現O(1)時間的查找。實踐證明，其效果是穩定、有效的。
並行遞推
對於同時支持中介數和遞推方法的全排列生成算法，我們可以同時利用中介數的有序性和遞推算法的高效性，從而設計出更加高效的加速框架。具體而言，我們可以改進隨機遞推方法，通過中介數的引用來使得各個核的任務量平均分配，從而實現全局效率的最最佳化。
考慮全排列算法A，其支持兩種操作：1、基於某個已有的排列P1，遞推出其下一個排列P2。2、基於某箇中介數I，通過映射產生出其對應的排列P。這樣，在進行了足夠的映射和遞推操作後，便可以產生所有的全排列。
與隨機遞推方法類似，可以看出，每個單獨的遞推過程是互不干擾的。不同之處在於，中介數的引入使得全排列的集合S成為一個全序集，從而我們可以迅速得到某個位置的排列。因而，我們可以通過計算和中介數映射使得每個遞推的種子均勻分布在集合中，保證每個核的工作量相同，從而避免多核中的木桶短板效應，實現效率的全局最最佳化。具體而言，其對應的算法框架如下：
1、對每個核，計算出其對應種子中介數的編號1，n!/m,2*n!/m,……這些編號均勻分布在1——n!上。
2、根據這些編號分別產生出每個核對應種子的中介數。
3、對於每個核，根據其中介數得到其遞推的種子排列。
4、每個核同時進行遞推操作，直到遞推了n!/m次為止。
5、合併所有核的計算結果。
可以看到，相比於隨機遞推方法，中介數的引入帶來了很大的優勢。首先，全排列與中介數的一一映射關係使得全排列集合成為全序集，從而可以保證每個核的運算量是相等的，避免了並行計算中任務分配不均勻帶來的短板效應。另一方面，每個核的任務均勻意味著可以提前知道每個核需要進行的遞推次數，從而避免了每一次遞推後都需要查看是否已經出現過的時間開銷，大大提升了效率。實踐證明，並行遞推的算法加速比是最高的。
完備性
由於所有全排列算法必須至少支持中介數映射或遞推操作中的一種，因而上面的加速框架可以適應所有的全排列生成算法，為其提供並行加速功能。
