定義
地統計學的主要理論是法統計學家G.Matheron創立的,經過不斷完善和改進,目前已成為具有堅實理論基礎和實用價值的數學工具。地統計學的套用範圍十分廣泛,不僅可以研究空間分布數據的結構性和隨機性、空間相關性和依賴性、空間格局與變異,還可以對空間數據進行最優無偏內插,以及模擬空間數據的離散性及波動性。地統計學由分析空間變異與結構的變異函式及其參數和空間局部估計的Kriging插值法兩個主要部分組成,目前已在地球物理、地質、生態、土壤等領域套用。氣象領域的套用目前還不多見,主要使用Kriging法進行降水、溫度等要素的最優內插的研究及氣候對農業影響方面的研究。
區域化變數理論
地統計學處理的對象為區域化變數,即在空間分布的變數。通常一個區域化變數具有兩個性質:①在局部的某一點,區域化變數的取值是隨機的;②對整個區域而言,存在一個總體或平均的結構,相鄰區域化變數的取值具有該結構所表達的相關關係。區域化變數的兩大特點是隨機性和結構性。基於此,地統計學引入隨機函式及其機率分布模型為理論基礎,對區域化變數加以研究。區域化變數可以看作是隨機變數的一個現實(realization)。對於隨機變數而言,必須在已知多個現實的前提下,才可以總結出其隨機函式的機率分布。
而對地學數據來講,往往我們只有一些採樣點,它們可以看作隨機變數的一個現實,所以也沒有辦法來推斷整個機率分布情況。為此,必須制定一些假設,即平穩性假設,假定在某個局部範圍內空間分布是均勻的。
理論核心
地統計學的主要用途,是研究對象空間自相關結構(或空間變異結構)的探測以及變數值的估計和模擬。不管哪一種用途,地統計學分析的核心是根據樣本點來確定研究對象(某一變數)隨空間位置而變化的規律,以此去推算未知點的屬性值。這個規律,就是變異函式。通常,我們利用採樣點及變異函式的計算公式得出樣本點的實驗變異函式(experimental variogram),擬合後的曲線為經驗變異函式。觀察該變異函式的分布圖像,尋找地統計學提供的某一種理論模型或者多個理論模型(basic model)的線性組合進行擬合。常見的理論模型有:線性模型、球狀模型、指數模型、高斯模型、冪指數模型等。
分析步驟
 地統計學分析步驟
地統計學分析步驟運用地統計學進行空間分析基本包括以下幾個步驟,即數據探索性分析,空間連續性的量化模型,未知點屬性值的估計,對未知點局部及空間整體不確定性的預測。用戶可根據自己的需要截止到中間某一項。數據探索性分析,主要是通過頻率分布圖、散點圖、位置圖等對數據的統計分布特徵做一個初步的考察。這個過程最容易發現的問題就是數據的集聚,以及異常點極值的出現。通常,可利用適當的變換,如對數變換來解決。
研究方法
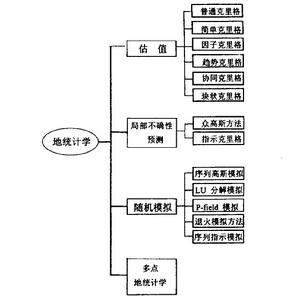
地統計學的研究方法包括局部估值、不確定性預測、隨機模擬及多點地統計學四部分。
一、估值(estimation)
地統計學最初套用是在礦產部門,作為礦產儲量計算的基本方法取得了相當豐碩的成果。在地統計學領域,克里格(Kriging)是大家公認的估計方法的總稱。實際上,它也是一種廣義的最小二乘回歸算法,而其最優目標定義為誤差的期望值為0,方差達到最小。包括簡單克里格(Simple Kriging)、普通克里格(Ordinary Kriging)、趨勢克里格
(Kriging with a trend model)、因子克里格(Factorial Kriging)、協同克里格(Co Kriging)、塊狀克里格(Block Krigin-g)等等。
二、局部不確定性預測(local uncertainty)
地統計學的估計功能主要是求得一個無偏的最優估值,同時給出每個估值的誤差方差,用以表示其不確定性。
這種方法的優點是比較簡單,只需要主變數之間的關聯關係。但其缺點是:
①認為誤差的分布是對稱的,但在實際情況中,低值區往往被高估,而高值區往往被低估。
②認為誤差的方差只依賴於真實值的形狀,而不考慮具體每個值的影響,即所謂的同方差性。
但實際上被一個大值和小值包圍的點,其估值的誤差一般要比被兩個同規模小值包圍估值點的誤差要大。所以,應確實考慮到所估計點周圍樣本點本身值的影響,即利用條件機率模型來推斷不確定性。通常有兩種方法:參數法(眾高斯方法)及非參數方法(指示克里格方法)。
眾高斯方法(MultiGaussianapproach):到目前為止,這是套用最廣泛的參數化方法。它假定所研究區域的機率分布可以用一個統一的公式表達,最終的機率依賴於相關參數。對應於眾高斯方法,即是均值和方差。我們利用克里格方法來估計這兩個參數,同時利用光滑樣本點頻率分布圖方式來平滑、增加其機率分布函式。
由於眾高斯方法要求多點分布必須是標準正態的,且沒有考慮極大值與極小值間的關聯關係。對於樣本點的指示變異函式不支持雙高斯分布,或者作為關鍵的輔助信息與主變數之間不滿足眾高斯分布,這時需採用指示克里格方法。
指示克里格(IndicatorKriging):利用指示克里格方法估計未知點的不確定性,首要的一步是將各種來源的信息進行指示編碼。即利用不同的閾值將原數據分為合適大小的間隔,考慮該間隔內點的關聯關係及其不同的關聯之間的關係。這樣,就有效地解決了眾高斯方法的缺點。
三、隨機模擬(simulation)
克里格方法完成了空間格局的認知,但沒能使其再現。通過克里格方法,可以獲得唯一的估計結果,而且極值點都被光滑下去。根據隨機變數的定義,每個變數可以有多個現實,也就是說每個未知點的估值可以有多種情況,但前提是總體趨勢的正確性,這種方法就是隨機模擬。隨機模擬可以利用各種不同類型數據(如“硬”的採樣點數據,“軟”的地震數據)再現已知的空間格局。“硬數據”指在採樣點精確測量的變數值。“軟數據”指關於該變數各種類型的間接測量值。隨機模擬可以生成眾多的現實,每一個現實展現同一種格局,但不同的表現方式。在單變數分布模型中,通過隨機變數的系列結果來統計其不確定性,與此類似,一系列隨機產生的現實,作為模型的輸入也可以表達輸出結果的不確定性。這些隨機現實是等機率的,即沒有哪一個現實是最好的。
四、多點地統計學(multi-point geostatistics)
多點地統計學的發展主要得益於地統計學在石油領域的套用。早期,地統計學多用於煤炭問題,通過塊狀估值得出可開採儲量。但在對石油儲區的研究中,人們發現單純的某個點的滲透性是沒有意義的,而應該以流的觀點來看待滲透性問題。這就使得對滲透性的連通性或其空間格局的量化比得到某局部點的精確值更為重要,而不是光滑的估計。傳統的地統計學藉助於煤炭科學的思想,利用變異函式來量化空間格局。但變異函式只能度量空間上兩個點之間的關聯,所以表現空間格局有很大的局限性。對於關聯性很強的情況,或所研究對象具備較為明顯的曲線特徵,這時要想量化其空間格局需要包含多個空間點。在圖像分析中,通過多點模板或者視窗來量化其格局。意識到變異函式在表達地質連續性上的局限性後,地統計學家將圖像分析中的思路借鑑過來,一個新的領域在地統計學中升起:多點地統計學。
原本地統計學模擬包括認知和再現兩部分。認知通過變異函式來完成,而再現通過序列高斯模擬的多個現實來完成。多點地統計學進一步改善了認知部分,即通過多個點的訓練圖像來取代變異函式,更有效地反映了研究目標的空間分布結構。而對於圖像分析而言,它只注重認知部分,但沒有再現功能。
多點地統計學的核心是訓練圖像。由於在地統計學中也出現過多點信息,但從未被量化過,而一般是將信息隱含的套用到具體問題模型中去。但如通過圖像的方式,可全面量化原數據各階的信息,因此我們可採用非條件的布爾方法得到訓練圖像再進行分析。
這種方法主要是在由於石油領域的問題引出,因此也主要套用在這個領域。包括理論本身,還有待於進一步完善。
GIS
GIS是對空間數據進行蒐集、存儲、檢索、轉換、顯示及分析的一門技術。它可以將具有地理坐標的數據信息作為一個專題層,或地圖文檔來進行管理。作為一個強大的資料庫系統,它可以存儲具有同樣空間範圍的多種專題信息。編輯、操作這些空間數據,對於現有的GIS軟體已不成問題,但對空間數據分布格局進行建模,抽取其特徵還很欠缺。這就需要像地質統計(geostatistics)這類空間分析的統計軟體包。地統計學近年來在國際上發展迅猛,特別是GIS的發展,對空間分析功能提出了一個新的要求,使得地統計學成為多個學科重視的焦點。但到目前為止,二者之間的結合還很少,或非常欠缺。如大型軟體ArcGis,從8版本以後加入了擴展模組,其中即有地統計學。但內容僅限於克里格系列方法,而對於模擬方法還是一片空白。所以,未來將兩者結合起來將是一種必然的趨勢。一種比較快捷的方式是利用組件式思想,將地統計學軟體內嵌到GIS軟體內部。這種結合方式要考慮到兩個原本不同系統的融合,所以稍顯繁瑣,且二者關係較為鬆散。但針對目前強大的需求,這無疑是一種多快好省的方法。
地統計模擬
模擬概念
模擬在廣義上是指使用模型複製現實的過程 。在地統計中,模擬是隨機函式(表面)的實現,其與生成該模擬的樣本數據擁有相同的地統計要素(使用均值、方差和半變異函式來度量)。更具體地說,高斯地統計模擬(GGS)適用於連續數據,並假設數據或數據的變換具有正態(高斯)分布。GGS所依託的主要假設是數據是靜態的-均值、方差和空間結構(半變異函式)在數據空間域上不發生改變。GGS的另一個主要假設是建模的隨機函式為多元高斯隨機函式。
同克里金法相比,GGS具有優勢。由於克里金法是基於數據的局部平均值的,因此,其可生成平滑的輸出。另一方面,GGS生成的局部變異性的製圖表達比較好,因為GGS將克里金法中丟失的局部變異性重新添加到了其生成的表面中。對於由GGS實現添加到特定位置的預測值中的變異性,其平均值為零,這樣,很多GGS實現的平均值會趨向於克里金預測。下圖對此概念進行了說明。各種實現以一組堆疊輸出圖層的形式表示出來,並且特定坐標位置的值服從高斯分布,其平均值等於該位置的克里金估計值,而擴散程度則由該位置上的克里金法方差給出。
提取值到表工具可以用來為上圖中的圖形生成數據,在對GGS生成的輸出進行後處理時該工具也很有用。
對GGS的使用在地統計實際操作中日益呈現出一種趨勢,它不是追求獲得每個未採樣位置的最佳無偏預測結果(正如克里金法所體現的),而是強調對決策分析和風險分析的不確定性的特證描述,這樣更適合於呈現數據中的全局趨勢(DeutschandJournel1998,Goovaerts1997)。模擬還會克服克里金估計值中的條件偏差帶來的問題(高值區域預測值通常偏低,而低值區域預測值通常偏高)。
對於所研究屬性的空間分布,地統計模擬可為其生成多個具有同等可能性的製圖表達。可基於這些製圖表達來測量未採樣位置的不確定性,這些未採樣位置在空間上被一起選取,而不是逐個被選取(如同通過克里金法方差進行測量一樣)。此外,克里金法方差通常獨立於數據值,且通常不能用作估計精度的測量值。另一方面,可以通過使用多個模擬實現(該實現用呈常態分配的輸入數據通過簡單克里金模型進行構建,即,數據呈常態分配或已使用常態得分變換或其他類型的變換對數據進行了變換)為未採樣位置的估計值構建分布來測量估計精度。對於使用估計數據值的風險評估和決策分析而言,這些不確定性的分布很關鍵。
GGS假設數據呈常態分配,但在實際中,很少會出現這種情況。對數據執行常態得分變換,使得數據符合標準常態分配(均值=0,方差=1)。然後對此常態分配數據進行模擬,並對結果做反向變換,以便以原始單位獲得模擬輸出。對常態分配數據使用簡單克里金法時,該克里金法所提供的克里金估計值和方差可完全定義研究區域中每個位置的條件分布。這樣,您可以在只知道每個位置的這兩個參數的情況下繪製隨機函式(未知採樣表面)的模擬實現,這也是GGS基於簡單克里金模型和常態分配數據的原因。
“高斯地統計模擬”工具支持兩種類型的模擬:
1、條件模擬遵循數據值(除非克里金模型中包含測量誤差)。由於模擬會在格網像元中心生成值,因此,如果此值與採樣點的位置不完全對應,則採樣位置的測量值與模擬值可能會不同。條件模擬也將以平均方式(即,在很多實現上平均)複製數據的均值、方差和半變異函式。模擬表面看起來很像克里金預測地圖,但其將顯示更多的空間變異性。
2、非條件模擬不遵循數據值,但會以平均方式複製數據的均值、方差和半變異函式。模擬表面所顯示的空間結構類似於克里金地圖,但輸入數據中存在高值或低值的地方不一定會出現高值和低值。
