簡介
一般線性模型或 多元回歸模型是一個統計線性模型。公式為:
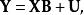 線性模型
線性模型其中 Y是具有一系列多變數測量的矩陣(每列是一個因變數的測量集合), X是獨立變數的觀察矩陣,其可以是設計矩陣(每列是關於一個自變數), B是包含通常要被估計的參數的矩陣,並且 U是包含誤差(噪聲)的矩陣。錯誤通常被認為是不相關的測量,並遵循多元常態分配。如果錯誤不遵循多元常態分配,廣義線性模型可以用來放鬆關於 Y和 U的假設。
一般線性模型包含了許多不同的統計模型:ANOVA,ANCOVA,MANOVA,MANCOVA,普通線性回歸,t檢驗和F檢驗。一般線性模型是多元線性回歸模型對多個因變數情況的推廣。如果 Y, B和 U是列向量,則上面的矩陣方程將表示多重線性回歸。
用一般線性模型進行的假設檢驗可以用兩種方法進行:多變數或多個獨立的單變數檢驗。在多元測試中, Y的列被一起測試,而在單變數測試中, Y的列被獨立地測試,即具有相同設計矩陣的多個單變數測試 。
多重線性回歸
多重線性回歸是一個一般化的線性回歸通過考慮多於一個的獨立變數,和一個特殊的情況下,通過限制相關的變數的數目,以形成一個一般的線性模型。線性回歸的基本模型是
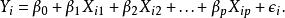 線性模型
線性模型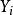 線性模型
線性模型在上面的公式中,我們考慮 n個因變數和 p個自變數的觀察值。因此,是因變數的觀察, X 是進行觀察的 j獨立變數, j= 1,2,..., p。值 β表示參數進行估計,並且 ε是獨立同分布正常的誤差 。
應用程式
一般線性模型的套用出現在科學實驗中的多個腦部掃描的分析中,其中 Y包含來自腦部掃瞄器的數據, X包含實驗設計變數和混淆。它通常以單變數的方式進行測試(在這種情況下通常稱為 質量單變數 ),通常稱為統計參數映射。