概述
樣本中各數據與樣本平均數的差的平方和的平均數叫做樣本方差;樣本方差的算術平方根叫做樣本標準差。樣本方差和樣本標準差都是衡量一個樣本波動大小的量,樣本方差或樣本標準差越大,樣本數據的波動就越大。 方差和標準差。方差和標準差是測算離散趨勢最重要、最常用的指標。方差是各變數值與其均值離差平方的平均數,它是測算數值型數據離散程度的最重要的方法。標準差為方差的平方根,用S表示。標準差相應的計算公式為 標準差與方差不同的是,標準差和變數的計算單位相同,比方差清楚,因此很多時候我們分析的時候更多的使用的是標準差。
 方差公式
方差公式公式標準差也被稱為標準偏差,或者實驗標準差,公式如圖。
簡單來說,標準差是一組數據平均值分散程度的一種度量。一個較大的標準差,代表大部分數值和其平均值之間差異較大;一個較小的標準差,代表這些數值較接近平均值。
例如,兩組數的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二個集合具有較小的標準差。
標準差可以當作不確定性的一種測量。例如在物理科學中,做重複性測量時,測量數值集合的標準差代表這些測量的精確度。當要決定測量值是否符合預測值,測量值的標準差占有決定性重要角色:如果測量平均值與預測值相差太遠(同時與標準差數值做比較),則認為測量值與預測值互相矛盾。這很容易理解,因為如果測量值都落在一定數值範圍之外,可以合理推論預測值是否正確。
標準差套用於投資上,可作為量度回報穩定性的指標。標準差數值越大,代表回報遠離過去平均數值,回報較不穩定故風險越高。相反,標準差數值越細,代表回報較為穩定,風險亦較小。
例如,A、B兩組各有6位學生參加同一次語文測驗,A組的分數為95、85、75、65、55、45,B組的分數為73、72、71、69、68、67。這兩組的平均數都是70,但A組的標準差為17.07分,B組的標準差為2.37分(此數據時在R統計軟體中運行獲得),說明A組學生之間的差距要比B組學生之間的差距大得多。
如是總體,標準差公式根號內除以n;
如是樣本,標準差公式根號內除以(n-1);
因為我們大量接觸的是樣本,所以普遍使用根號內除以(n-1)。
定義
設X是一個隨機變數,若E{[X-E(X)]^2}存在,則稱E{[X-E(X)]^2}為X的方差,記為D(X),Var(X)或DX。
即D(X)=E{[X-E(X)]^2}稱為方差,而σ(X)=D(X)^0.5(與X有相同的量綱)稱為標準差(或均方差)。即用來衡量一組數據的離散程度的統計量。
方差刻畫了隨機變數的取值對於其數學期望的離散程度。(標準差.方差越大,離散程度越大。否則,反之)
若X的取值比較集中,則方差D(X)較小,
若X的取值比較分散,則方差D(X)較大。
因此,D(X)是刻畫X取值分散程度的一個量,它是衡量X取值分散程度的一個尺度。
所有數減去其平均值的平方和,所得結果除以該組數之個數(或個數減一),再把所得值開根號,所得之數就是這組數據的標準差。
數據意義
標準差越高,表示實驗數據越離散,也就是說越不精確。
反之,標準差越低,代表實驗的數據越精確。
離散度
標準差是反應一組數據離散程度最常用的一種量化形式,是表示精密確的最要指標。說起標準差首先得搞清楚它出現的目 的。我們使用方法去檢測它,但檢測方法總是有誤差的,所以檢測值並不是其真實值。檢測值與真實值之間的差距就是評價檢測方法最有決定性的指標。但是真實值 是多少,不得而知。因此怎樣量化檢測方法的準確性就成了難題。這也是臨床工作質控的目的:保證每批實驗結果的準確可靠。
雖然樣本的真實值是不可能知道的,但是每個樣本總是會有一個真實值的,不管它究竟是多少。可以想像,一個好的檢測方法,基檢測值應該很緊密的分散在真實值周圍。如何不緊密,那距真實值的就會大,準確性當然也就不好了,不可能想像離散度大的方法,會測出準確的結果。因此,離散度是評價方法的好壞的 最重要也是最基本的指標。
一組數據怎樣去評價和量化它的離散度呢?人們使用了很多種方法:
一、極差:
最直接也是最簡單的方法,即最大值-最小值(也就是極差)來評價一組數據的離散度。這一方法在日常生活中最為常見,比如比賽中去掉最高最低分就是極差的具體套用。
二、離均差的平方和:
由於誤差的不可控性,因此只由兩個數據來評判一組數據是不科學的。所以人們在要求更高的領域不使用極差來評判。其實,離散度就是數據偏離平均值的程度。因此將數據與均值之差(我們叫它離均差)加起來就能反映出一個準確的離散程度。和越大離散度也就越大。
但是由於偶然誤差是成常態分配的,離均差有正有負,對於大樣本離均差的代數和為零的。為了避免正負問題,在數學有上有兩種方法:一種是取絕對 值,也就是常說的離均差絕對值之和。而為了避免符號問題,數學上最常用的是另一種方法--平方,這樣就都成了非負數。因此,離均差的平方和成了評價離散度 一個指標。
三、方差(S2):
由於離均差的平方和與樣本個數有關,只能反應相同樣本的離散度,而實際工作中做比較很難做到相同的樣本,因此為了消除樣本個數的影響,增加可比性,將標準差求平均值,這就是我們所說的方差成了評價離散度的較好指標。 樣本量越大越能反映真實的情況,而算數均值卻完全忽略了這個問題,對此統計學上早有考慮,在統計學中樣本的均差多是除以自由度(n-1),它是意思是樣本能自由選擇的程度。當選到只剩一個時,它不可能再有自由了,所以自由度是n-1。
四、標準差(SD):
由於方差是數據的平方,與檢測值本身相差太大,人們難以直觀的衡量,所以常用方差開根號換算回來這就是我們要說的標準差。
在統計學中樣本的均差多是除以自由度(n-1),它是意思是樣本能自由選擇的程度。當選到只剩一個時,它不可能再有自由了,所以自由度是n-1。
五、變異係數(CV):
標準差能很客觀準確的反映一組數據的離散程度,但是對於不同的檢目,或同一項目不同的樣本,標準差就缺乏可比性了,因此對於方法學評價來說又引入了變異係數(CV)。
方差的種類及計算
離散型方差
離散型方差的計算式為:
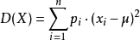
, 其中
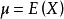
而將上式展開後可得:
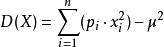
連續型方差
連續型方差的計算式為:
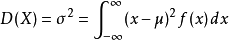
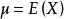
將上式展開後可得:
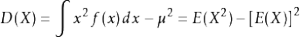
以上兩式是一樣的,只是寫法不同。
證明:由數學期望的性質得
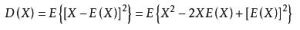
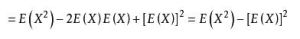
計算
 常用計算公式
常用計算公式由定義知,方差是隨機變數 X 的函式g(X)=∑[X-E(X)]^2 pi,數學期望。如圖:
由方差的定義可以得到以下常用計算公式:
D(X)=∑xi²pi-E(x)²
D(X)=∑(xi²pi+E(X)²pi-2xipiE(X));
=∑xi²pi+∑E(X)²pi-2E(X)∑xipi;
=∑xi²pi+E(X)²-2E(X)²;
=∑xi²pi-E(x)²
方差其實就是標準差的平方。
方差的性質
1.設c是常數,則D(C)=0
2.設X是隨機變數,c是常數,則有
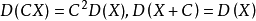
3.設 X 與 Y 是兩個隨機變數,則
D(X+Y)= D(X)+D(Y)+2Cov(X,Y)
D(X -Y)= D(X)+D(Y)-2Cov(X,Y)
特別的,當X,Y是兩個不相關的隨機變數則
D(X+Y)=D(X)+D(Y),D(X-Y)=D(X)+D(Y),
此性質可以推廣到有限多個兩兩不相關的隨機變數之和的情況。
4.D(X)=0的充分必要條件是X以機率為1取常數值c,即X=c,a.s.其中E(X)=c。
5.D(aX+bY)=aDX+bDY+2abCov(X,Y)。
隨機變數期望和方差求解公式隨機變數X。
X服從兩點分布,則E(X)=p D(X)=p(1-p)
X服從泊松分布,即X~ π(λ),則 E(X)= λ,D(X)= λ
X服從均勻分布,即X~U(a,b),則
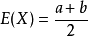
X服從指數分布,即X~e(λ), E(X)= 1/λ,D(X)= 1/λ
X服從二項分布,即X~B(n,p),則E(x)=np, D(X)=np(1-p)
X 服從常態分配,即X~N(μ,σ), 則E(x)=μ, D(X)=σ
X 服從標準常態分配,即X~N(0,1), 則E(x)=0, D(X)=1
隨機變數求方差的通用公式,即D(X)=E(X)-[E(X)]
舉例
如下面的例子:
已知某零件的真實長度為a,現用甲、乙兩台儀器各測量10次,將測量結果X用坐標上的點表示如圖:
甲儀器測量結果:
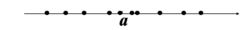 方差
方差乙儀器測量結果:全是a
兩台儀器的測量結果的均值都是 a 。但是用上述結果評價一下兩台儀器的優劣,很明顯,我們會認為乙儀器的性能更好,因為乙儀器的測量結果集中在均值附近。
由此可見,研究隨機變數與其均值的偏離程度是十分必要的。那么,用怎樣的量去度量這個偏離程度呢?容易看到E[|X-E[X]|]能度量隨機變數與其均值E(X)的偏離程度。但由於上式帶有絕對值,運算不方便,通常用量E[(X-E[X])] 這一數字特徵就是方差。
公式
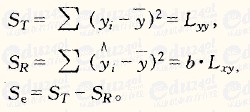 方差
方差方差是實際值與期望值之差平方的平均值,而標準差是方差算術平方根。
在實際計算中,我們用以下公式計算方差。
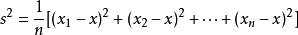 方差
方差方差是各個數據與平均數之差的平方的和的平均數,即
,其中,x表示樣本的平均數,n表示樣本的數量,x表示個體,而s^2就表示方差。
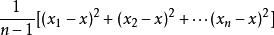 方差
方差而當用
作為樣本X的方差的估計時,發現其數學期望並不是X的方差,而是X方差的
倍,
的數學期望才是X的方差,用它作為X的方差的估計具有“無偏性”,所以我們總是用
來估計X的方差,並且把它叫做“樣本方差”。
方差,通俗點講,就是和中心偏離的程度!用來衡量一批數據的波動大小(即這批數據偏離平均數的大小)並把它叫做這組數據的方差。記作S。 在樣本容量相同的情況下,方差越大,說明數據的波動越大,越不穩定。
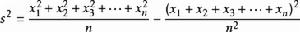 方差
方差公式可以進一步推到為:
其中x為這組數據中的數據,n為大於0的整數。
統計學
數據波動
當數據分布比較分散(即數據在平均數附近波動較大)時,各個數據與平均數的差的平方和較大,方差就較大;當數據分布比較集中時,各個數據與平均數的差的平方和較小。因此方差越大,數據的波動越大;方差越小,數據的波動就越小。
樣本中各數據與樣本平均數的差的平方和的平均數叫做樣本方差;樣本方差的算術平方根叫做樣本標準差。樣本方差和樣本標準差都是衡量一個樣本波動大小的量,樣本方差或樣本標準差越大,樣本數據的波動就越大。
方差和標準差是測算離散趨勢最重要、最常用的指標。方差是各變數值與其均值離差平方的平均數,它是測算數值型數據離散程度的最重要的方法。標準差為方差的算術平方根,用S²表示。方差相應的計算公式為
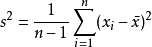 方差
方差標準差與方差不同的是,標準差和變數的計算單位相同,比方差清楚,因此很多時候我們分析的時候更多的使用的是標準差。
聯考實例
(甘肅省,2002年)某校初三年級甲、乙兩班舉行電腦漢字輸入速度比賽,兩個班參加比賽的學生每分鐘輸入漢字的個數,經統計和計算後結果如下表所示:
| 班級 | 參加人數 | 平均字數 | 中位數 | 方差 |
|---|---|---|---|---|
| 甲 | 55 | 135 | 149 | 191 |
| 乙 | 55 | 135 | 151 | 110 |
有一位同學根據上表得出如下結論:
①甲、乙兩班學生的平均水平相同
②乙班優秀的人數比甲班優秀的人數多(每分鐘輸入漢字達150個以上為優秀)
③甲班學生比賽成績的波動比乙班學生比賽成績的波動大。上述結論正確的是________(填序號)。
解:填①、②、③,
解:甲乙的平均數相同,所以①甲、乙兩班學生的平均水平相同.根據中位數可知乙的中位數大,所以②乙班優秀的人數比甲班優秀的人數多。第三題,根據方差數據可知,方差越大波動越大,反之越小,所以甲班學生比賽成績的波動比乙班學生比賽成績的波動大。
故填:①②③.
點評:本題考查統計知識中的中位數、平均數和方差的意義。要知道平均數和中位數反映的是數據的集中趨勢,方差反映的是離散程度。
極差與方差
極差不能用作比較,單位不同 ; 方差能用作比較, 因為都是個比率。
標準差
一組數據的平均值及標準差常常同時做為參考的依據。在直覺上,如果數值的中心以平均值來考慮,則標準差為統計分布之一“自然”的測量。
定義公式
標準差公式
1、方差s^2=[(x1-x)^2+(x2-x)^2+......(xn-x)^2]/n
2、標準差=方差的算術平方根
幾何學解釋
從幾何學的角度出發,標準差可以理解為一個從 n 維空間的一個點到一條直線的距離的函式。舉一個簡單的例子,一組數據中有3個值,X1,X2,X3。它們可以在3維空間中確定一個點 P = (X1,X2,X3)。想像一條通過原點的直線 。如果這組數據中的3個值都相等,則點 P 就是直線 L 上的一個點,P 到 L 的距離為0, 所以標準差也為0。若這3個值不都相等,過點 P 作垂線 PR 垂直於 L,PR 交 L 於點 R,則 R 的坐標為這3個值的平均數:公式運用一些代數知識,不難發現點 P 與點 R 之間的距離(也就是點 P 到直線 L 的距離)是。在 n 維空間中,這個規律同樣適用,把3換成 n 就可以了。
標準差與標準誤的區別
標準差與標準誤都是心理統計學的內容,兩者不但在字面上比較相近,而且兩者都是表示距離某一個標準值或中間值的離散程度,即都表示變異程度,但是兩者是有著較大的區別的。 首先要從統計抽樣的方面說起。現實生活或者調查研究中,我們常常無法對某類欲進行調查的目標群體的所有成員都加以施測,而只能夠在所有成員(即樣本)中抽取一些成員出來進行調查,然後利用統計原理和方法對所得數據進行分析,分析出來的數據結果就是樣本的結果,然後用樣本結果推斷總體的情況。一個總體可以抽取出多個樣本,所抽取的樣本越多,其樣本均值就越接近總體數據的平均值。
標準差的意義
標準差表示的就是樣本數據的離散程度。標準差就是樣本平均數方差的開平方,標準差通常是相對於樣本數據的平均值而定的,通常用M±SD來表示,表示樣本某個數據觀察值相距平均值有多遠。從這裡可以看到,標準差收到極值的影響。標準差越小,表明數據越聚集;標準差越大,表明數據越離散。標準差的大小因測驗而定,如果一個測驗是學術測驗,標準差大,表示學生分數的離散程度大,更能夠測量出學生的學業水平;如果一個側樣測量的是某種心理品質,標準差小,表明所編寫的題目是同質的,這時候的標準差小的更好。標準差與常態分配有密切聯繫:在常態分配中,1個標準差等於常態分配下曲線的68.26%的面積,1.96個標準差等於95%的面積。

