閔科夫斯基空間
正文
愛因斯坦狹義相對論的時空模型。物理學上稱為閔科夫斯基時空,它是德國數學家H.閔科夫斯基為適應狹義相對論的需要而提出來的。一般說來,n 維的閔科夫斯基空間R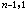 是n維歐氏空間En的一個變種,和n維歐氏空間一樣,R
是n維歐氏空間En的一個變種,和n維歐氏空間一樣,R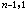 的基本幾何元素是點和向量,其中照樣有直線和各種不同維數的平面等幾何圖形。狹義相對論中採用的是四維時空R3,1。
的基本幾何元素是點和向量,其中照樣有直線和各種不同維數的平面等幾何圖形。狹義相對論中採用的是四維時空R3,1。 R
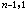 的任何兩個向量l,m也有數量積l·m,一個向量也有其長度的平方l2=l·l,從而也有向量的正交性的概念,但和歐氏空間En的基本區別在於,在R
的任何兩個向量l,m也有數量積l·m,一個向量也有其長度的平方l2=l·l,從而也有向量的正交性的概念,但和歐氏空間En的基本區別在於,在R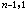 中,若l 是非零向量,l2不常常是正的。更具體地說,在n 個相互正交的線性無關的單位向量組(e1,e2,…,en)中,有n-1個向量的長度平方為 +1,有一個向量的長度平方為-1。設其中e1,e2,…,en-1的長度平方為+1,而en的長度平方為-1,這樣的(e1,e2,…,en)就稱為標準正交基,參考於這一組基,向量l 和m可分別表示為
中,若l 是非零向量,l2不常常是正的。更具體地說,在n 個相互正交的線性無關的單位向量組(e1,e2,…,en)中,有n-1個向量的長度平方為 +1,有一個向量的長度平方為-1。設其中e1,e2,…,en-1的長度平方為+1,而en的長度平方為-1,這樣的(e1,e2,…,en)就稱為標準正交基,參考於這一組基,向量l 和m可分別表示為 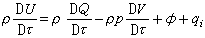
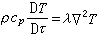 ,
,
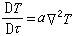 ,
,
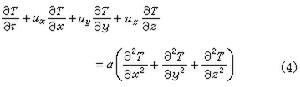 。
。
在閔科夫斯基空間中,把標準正交基{e1,e2,…,en}變到另一組標準正交基的線性變換A稱為洛倫茨變換,洛倫茨變換所成的群稱為洛倫茨群,記為O(n-1,1),參考於標準正交基,洛倫茨群的元素可用n×n陣A=(αij)表示,這裡αij是由
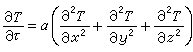
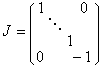 ,
,
A*JA=J。
這裡A*是A 的轉置,所以洛倫茨群O(n-1, 1)也指滿足A*JA=J 的n×n陣A的全體,一組標準正交基添上一個定點作為原點就構成R n-1,1的一個洛倫茨標架,參考於洛倫茨標架,可以得出R 中的點P 的坐標(x1,x2,…,xn),變換
中的點P 的坐標(x1,x2,…,xn),變換 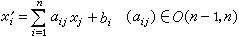
過一定點(
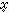 1,
1,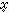 2,…,
2,…,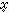 4)的光錐的方程是
4)的光錐的方程是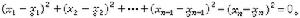 在任一非齊次的洛倫茨變換下,光錐仍變為光錐。
在任一非齊次的洛倫茨變換下,光錐仍變為光錐。 和歐氏空間En一樣,R
 有很豐富的幾何內容,由於O(n-1,1)比正交群O(n)複雜得多,R
有很豐富的幾何內容,由於O(n-1,1)比正交群O(n)複雜得多,R 的幾何學比En的幾何學複雜得多。
的幾何學比En的幾何學複雜得多。 在古典的時空觀念中,時間和空間是分立的,現實空間的模型是三維的歐幾里得空間,時間是一維的數軸,兩個事件的同時性是絕對的,也就是說,不論用什麼方式去測量,兩個事件的同時性是不可改變的,這種時空觀念和牛頓力學十分協調,但和J.C.麥克斯韋的電磁場理論卻不相協調,這因為,如令光速為常數,麥克斯韋方程是在洛倫茨變換下不變的,但洛倫茨變換會變更兩個不在同一地點發生的事件的同時性,米切爾森-莫里實驗指示了光速不因光源的運動速度而變化,使人們不得不去修正牛頓力學而導致了愛因斯坦狹義相對論的出現。
在狹義相對論中,採取四維的閔科夫斯基時空為現實時空的模型,對於一個固定的慣性測量系統(即洛倫茨標架)來說,(x1,x2,x3,x4)表示一個時空點,說明一個事件在何時何地發生:x1,x2,x3表示位置,x4=сt表示時間(這裡c為光速,是不變的正常數),在一點的光錐把以這點為始點的向量分為五類(見表
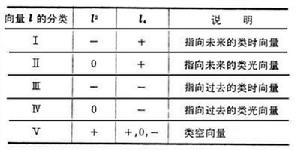 )。
)。 粒子的運動可由R3,1中的曲線表示,稱為世界線,它的切向量必須不是類空的,可規定它是指向未來的向量,如果它屬於第Ⅰ類,則它的速度小於光速,如果它屬於第Ⅱ類,它的速度等於光速。它不可能是屬於第Ⅴ類的,意義是:粒子運動的速度不能大於光速。另一面,如果P 與P1是R3,1中兩點,若向量捗屬於第Ⅰ或第Ⅱ類,則P1必為P 的未來。若捗屬於第Ⅲ、Ⅳ類,則P1必為P的過去。若
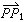 屬於第Ⅴ類,則必存在一個洛倫茨標架,使P 和P1具同時性。
屬於第Ⅴ類,則必存在一個洛倫茨標架,使P 和P1具同時性。 使Л4的符號不變的洛倫茨變換(非齊次)稱為正常的。狹義相對論要求物理定律在正常洛倫茨變換下為不變的,J.C.麥克斯韋的電磁場理論已適合這個要求,而I.牛頓的經典力學作了修正之後,也能符合這個要求。
由於運用了閔科夫斯基空間R3,1作為時空模型,愛因斯坦狹義相對論就有了很好的敘述方式,對於現代物理學的發展起了很大的作用。有了閔科夫斯基時空之後,愛因斯坦又進一步研究了引力場理論,即廣義相對論,從而引入洛倫茨流形的概念,閔科夫斯基時空是曲率張量為0的洛倫茨流形,因而閔科夫斯基時空與歐氏空間均為平坦空間,而不是彎曲的。