概述
實投影平面可以看作是一個具有額外點的歐氏平面,這些點稱之為無窮遠點,並被認為是位於一條新的線上(該線稱之為無窮遠線)。每一個無窮遠點對應至一個方向(由一條線之斜率給出),可非正式地定義為一個點自原點朝該方向移動之極限。在歐氏平面里的平行線可看成會在對應其共同方向之無窮遠點上相交。給定歐氏平面上的一點( x, y),對任意非零實數 Z,三元組( xZ, yZ, Z)即稱之為該點的齊次坐標。依據定義,將齊次坐標內的數值乘上同一個非零實數,可得到同一點的另一組齊次坐標。例如,笛卡兒坐標上的點 (1,2) 在齊次坐標中即可標示成 (1,2,1) 或 (2,4,2)。原來的笛卡兒坐標可透過將前兩個數值除以第三個數值取回。因此,與笛卡兒坐標不同,一個點可以有無限多個齊次坐標表示法。
一條通過原點(0, 0)的線之方程可寫作 nx+ my= 0,其中 n 及 m 不能同時為 0。以參數表示,則能寫成 x= mt, y= − nt。令 Z=1/t,則線上的點之笛卡兒坐標可寫作( m/ Z, − n/ Z)。在齊次坐標下,則寫成( m, − n, Z)。當 t 趨向無限大,亦即點遠離原點時,Z 會趨近於 0,而該點的齊次坐標則會變成( m, − n, 0)。因此,可定義( m, − n, 0)為對應 nx+ my= 0這條線之方向的無窮遠點之齊次坐標。因為歐氏平面上的每條線都會與透過原點的某一條線平行,且因為平行線會有相同的無窮遠點,歐氏平面每條線上的無窮遠點都有其齊次坐標。
概括來說:
•投影平面上的任何點都可以表示成一三元組(X,Y,Z),稱之為該點的'齊次坐標或投影坐標,其中 X、Y 及 Z 不全為 0。
•以齊次坐標表表示的點,若該坐標內的數值全乘上一相同非零實數,仍會表示該點。
•相反地,兩個齊次坐標表示同一點,若且唯若其中一個齊次坐標可由另一個齊次坐標乘上一相同非零常數得取得。
•當 Z 不為 0,則該點表示歐氏平面上的該(X/Z,Y/Z)。
•當 Z 為 0,則該點表示一無窮遠點。
注意,三元組(0, 0, 0)不表示任何點。原點表示為(0, 0, 1)。
符號
有些作者會使用不同的符號表示齊次坐標,以與笛卡兒坐標相區別,如以冒號代替逗號,以 (x:y:z) 代替( x, y, z),以強調該坐標有著比例的性質。亦有以方括弧代替括弧,以[ x, y, z]來強調有多個坐標表示同一個點。有些作者則會同時使用冒號與方括弧,如 [x:y:z]。
其他投影空間
齊次坐標的數值若為實數,則會得出一般實投影空間內的一個點。不過,該數值可以為任意的體,特別是在復投影空間裡,使用的數值為複數。例如,復投影線在齊次坐標中以兩個數值表示之,稱之為黎曼球面。其他的體,包括有限體,也都可以被使用。
用於投影空間的齊次坐標亦可使用除環來建立。不過,在此情況下,必須小心考慮其乘法可能是不可交換的。
重要性
《計算機圖形學(OpenGL版)》的作者F.S. Hill Jr.曾說過一句話:
“齊次坐標表示是計算機圖形學的重要手段之一,它既能夠用來明確區分向量和點,同時也更易用於進行仿射(線性)幾何變換。”
於是我們知道,其重要性,主要有二,其一是區分向量和點,其二是易於進行仿射變化(Affine Transformation) 。
套用
齊次坐標在電腦圖形內無處不在,因為該坐標允許平移、旋轉、縮放及透視投影等可表示為矩陣與向量相乘的一般向量運算。依據鏈式法則,任何此類運算的序列均可相乘為單一個矩陣,從而實現簡單且有效之處理。與此相反,若使用笛卡兒坐標,平移及透視投影不能表示成矩陣相乘,雖然其他的運算可以。現在的OpenGL及Direct3D圖形卡均利用齊次坐標的優點,以具4個暫存器的向量處理器來實作頂點著色引擎。
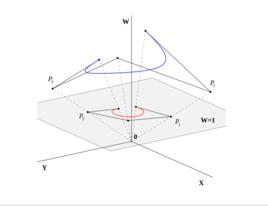
例如,在透視投影里,空間中的位置與該位置至稱為“投影中心”的固定點間的線相關聯。該點可透過找出平面與該線之相交點被映射至該平面上。這是三維物件如何呈現於眼上的一精確表示。在最簡單的情況下,投影中心會是圓點,而點會映射至平面 z= 1上,如同在笛卡兒坐標上時一樣。對空間內的一點( x, y, z),其線與平面相交的點為( x/ z, y/ z, 1)。刪掉現在顯得多餘的 z 坐標,即變成( x, y, z)。在齊次坐標里,點( x, y, z)表示為( xw, yw, zw, w),且該點映射至平面上的點表示為( xw, yw, zw),因此投影可以以矩陣形成表示為
 齊次坐標
齊次坐標表示其他幾何變轉的矩陣可與此一矩陣透過矩陣乘法結合。其結果是,任何空間的透視投影都能被表示為單一個矩陣 。
示例
例如,二維點(x,y)的齊次坐標表示為(hx,hy,h)。由此可以看出,一個向量的齊次表示是不唯一的,齊次坐標的h取不同的值都表示的是同一個點,比如齊次坐標(8,4,2)、(4,2,1)表示的都是二維點(4,2)。
給出點的齊次表達式[X Y H],就可求得其二維笛卡爾坐標,即
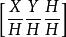 齊次坐標
齊次坐標[X Y H]→ = [x y 1], 這個過程稱為歸一化處理。
在幾何意義上,相當於把發生在三維空間的變換限制在H=1的平面內。
那么引進齊次坐標有什麼必要,它有什麼優點呢?
許多圖形套用涉及到幾何變換,主要包括平移、旋轉、縮放。以矩陣表達式來計算這些變換時,平移是矩陣相加,旋轉和縮放則是矩陣相乘,綜合起來可以表示為p' = m1*p+ m2(註:因為習慣的原因,實際使用時一般使用變化矩陣左乘向量)(m1旋轉縮放矩陣, m2為平移矩陣, p為原向量 ,p'為變換後的向量)。引入齊次坐標的目的主要是合併矩陣運算中的乘法和加法,表示為p' = p*M的形式。即它提供了用矩陣運算把二維、三維甚至高維空間中的一個點集從一個坐標系變換到另一個坐標系的有效方法。
其次,它可以表示無窮遠的點。n+1維的齊次坐標中如果h=0,實際上就表示了n維空間的一個無窮遠點。對於齊次坐標(a,b,h),保持a,b不變,| V|=(x1*x1,y1*y1,z1*z1)^1/2的過程就表示了標準坐標系中的一個點沿直線 ax-by=0 逐漸走向無窮遠處的過程。