定義
微分幾何學的一個分支。是在20世紀初期依據F.克萊因的思想開始發展起來的，研究的對象主要是曲線、曲面、共軛網等在射影變換群下的不變數、協變圖形及其性質。G.達布的有名的曲面論這部著作中，蘊含了它的萌芽。到20世紀的40年代為止，概括起來，大致有三種討論的方法，其內容也隨著這些方法的建立而趨於完善。
第一種是以G.富比尼為首的義大利學派的方法。試以曲面論為例進行說明。 設(x)=(x1,x4,x3,x4)是三維射影空間p3 的點的齊次坐標, x=x(u,υ)是一個曲面S的參數表示。用一種射影不變的方法確定x的比例因子,從而獲得 G.富比尼的規範坐標。 其次，按照規範坐標的表示x(u,υ)還可構造二次和三次的基本形式：
式中φ和普通曲面論中的第二基本形式只相差一個因子，於是φ＝0定義了曲面的兩系主切（或漸近）曲線,ψ和φ滿足配極關係，而且ψ＝0定義了曲面的三系達布曲線。這二個基本形式的係數必須滿足一系列的關係式，即所謂曲面的基本方程。同普通曲面論的場合一樣，可導出射影曲面論的基本定理，給定了兩個微分形式φ和ψ，並設它們的係數滿足上述的基本方程，那么，除了射影變換外，可以惟一地決定一個曲面，使它的兩個基本形式是φ和ψ。
第二種是É.嘉當繼承達布後創新的活動標架法。他重新建立起射影曲面論，這比起第一種來，既簡練，又富有廣泛性。所論的問題都被歸結為一個普法夫方程系統，它的可積分條件被寫成嘉當結構方程，而且許多結果就從此自然地被推導出來。
以n維射影空間pn (n≥3)的共軛網A0(u,υ)為例。設這網沿方向u的拉普拉斯變換是A-1,A-2,…,A-m，…,而且沿方向υ的是A1,A2,…,Am ,…,則有
式中假定αrbr≠0。如果用É.嘉當的外形式法來表達,上列方程組便可歸結為普法夫方程組
式中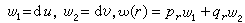
此時,É.嘉當結構方程除了從定義得到的
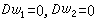(D表示外微分)之外，可還有寫成外積形式的方程：
近年來發展起來的高維射影空間共軛網理論，就是這樣根據É.嘉當的外形式法建立的。
最後第三種是中國學者在20世紀30年代末期開創而發展起來的所謂結構式射影微分幾何，主要是用幾何作圖法來建立射影協變的構圖和不變數，例如，用平面曲線在其某種奇異點的不變數以表達其他幾何不變數，就是一項具有代表性的顯著的成果。
影響
公式射影微分幾何學的研究對數學其他分支以及力學、物理學、工程學等的影響是不可估量的。如：偽球面上的幾何與非歐幾何有密切關係；測地線和力學、變分學、拓撲學等有著深刻的聯繫，是內容豐富的研究課題。這方面有以J.阿達馬、H.龐加萊等人為首的優異研究。極小曲面是和複變函數論、變分學、拓撲學關係極為深刻的研究領域，K.魏爾斯特拉斯、J.道格拉斯等人作出過卓越貢獻。
射影微分幾何學的研究工具大部分是微積分學。力學、物理學、天文學以及技術和工業的日益增長的要求則是微分幾何學發展的重要因素。儘管微分幾何學主要研究三維歐幾里得空間中的曲線、曲面的局部性質，但它形成了現代微分幾何學的基礎則是毋庸置疑的。因為依賴於圖形的直觀性及由它進行類推的方法，即使在今天也未失其重要性。
和分析學新的結合
射影微分幾何學的研究與發展離不開微分方程，達布的《曲面論》一書就包含了豐富的古典微分方程的內容。É.嘉當和凱勒所發展的外微分方程理論，對於解析函式領域的一大類局部微分幾何問題，給出了一般的有效的方法。
整體微分幾何的發展，需要運用更深入的，現代化的分析工具，特別是偏微分方程理論以及與之有關的非線性分析。
線上性理論中，一個突出的成果是阿蒂亞和辛格的指標定理，緊緻微分流形上的一個線性橢圓運算元的零空間的維數與象空間的維數都是有限數,其差稱為指標,這個定理指出，這種指標可以表示為和流形（或纖維叢）及橢圓運算元有關的拓撲不變數,而過去的黎曼-羅赫定理，希策布魯赫的指標定理等都是它的特殊情形。這個定理對於確定楊-米爾斯方程的解的存在性和其自由度,起了重要作用。此外，流形上的拉普拉斯運算元的特徵值的研究也是一個重要方面。
射影微分幾何學所遇到的偏微分方程大多是非線性的，調和函式的概念被推廣成黎曼流形間的調和映射，它聯繫於一個推廣的狄利克雷積分的變分問題，其歐拉方程是非線性的橢圓型方程組，J.伊爾斯等人用了多種分析的技巧證明了各種存在性和不存在性定理,近年來,R.舍恩和K.K.烏倫貝克又對廣義解的奇性作了深入的分析。極小曲面理論近年來得到更深入的發展，研究範圍日趨廣泛，而且對流形的拓撲以及廣義相對論中的數學問題均有重要套用。在調和映射、極小曲面，以及其他許多微分幾何問題上,大範圍變分方法成了重要工具,非線性泛函的極小元素或臨界元素的正則性和存在性起了很大作用。如果考慮洛倫茨流形到黎曼流形的調和映射，就歸結為雙曲型偏微分方程的整體解的存在性問題，這方面成果國際上較少，谷超豪證明了閔科夫斯基平面到完備黎曼流形的調和映射的柯西問題的整體存在性定理，某些調和映射在物理學中稱為非線性σ模型,是物理學家獨立地提出的。
有些射影微分幾何學問題還必須求解“真正”非線性偏微分方程，這是比擬線性方程的非線性程度更高的偏微分方程，其難度更大，突出的事項是丘成桐解決了由卡拉皮所提出的一個猜想,證明了某種愛因斯坦-凱勒流形的存在定理，這需要求解復的蒙日-安培方程,它的非線性程度更高，需要有高度的分析技巧。丘成桐還解決了一系列的其他的與非線性偏微分方程有關的幾何問題。
具有復結構的微分流形特別是凱勒流形在多元複變函數和代數幾何中起著重要的作用。
其它學科的聯繫
射影微分幾何學射影微分幾何學的產生和發展是和數學分析密切相連的。在這方面第一個做出貢獻的是瑞士數學家歐拉。1736年他首先引進了平面曲線的內在坐標這一概念，即以曲線弧長這以幾何量作為曲線上點的坐標，從而開始了曲線的內在幾何的研究。
十八世紀初，法國數學家蒙日首先把微積分套用到曲線和曲面的研究中去，並於1807年出版了它的《分析在幾何學上的套用》一書，這是微分幾何最早的一本著作。在這些研究中，可以看到力學、物理學與工業的日益增長的要求是促進微分幾何發展的因素。
高斯貢獻
1827年，高斯發表了《關於曲面的一般研究》的著作，這在微分幾何的歷史上有重大的意義，它的理論奠定了現代形式曲面論的基礎。微分幾何發展經歷了150年之後，高斯抓住了微分幾何中最重要的概念和帶根本性的內容，建立了曲面的內在幾何學。其主要思想是強調了曲面上只依賴於第一基本形式的一些性質，例如曲面上曲面的長度、兩條曲線的夾角、曲面上的一區域的面積、測地線、測地線曲率和總曲率等等。他的理論奠定了近代形式曲面論的基礎。
克萊因貢獻
射影微分幾何學1872年克萊因在德國埃爾朗根大學作就職演講時，闡述了《埃爾朗根綱領》，用變換群對已有的幾何學進行了分類。在《埃爾朗根綱領》發表後的半個世紀內，它成了幾何學的指導原理，推動了幾何學的發展，導致了射影微分幾何、仿射微分幾何、共形微分幾何的建立。特別是射影微分幾何起始於1878年阿爾方的學位論文，後來1906年起經以威爾辛斯基為代表的美國學派所發展，1916年起又經以富比尼為首的義大利學派所發展。
隨後，由於黎曼幾何的發展和愛因斯坦廣義相對論的建立，射影微分幾何學在黎曼幾何學和廣義相對論中的得到了廣泛的套用，逐漸在數學中成為獨具特色、套用廣泛的獨立學科。
參考書目
蘇步青著：《射影曲面概論》，上海科學技術出版社，上海，1964。
蘇步青著：《射影共軛網概論》，上海科學技術出版社，上海，1978。
