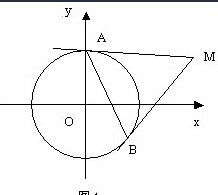
圓的切線方程
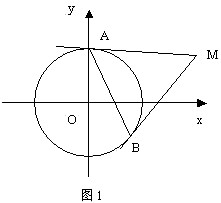過圓外一點的2條切線若點O(x0,y0)在圓x^2+y^2+Dx+Ey+F=0上,，
則過點P的切線方程為
x0 x + y0 y + D*(x+x0)/2 + E*(y+y0)/2 + F =0
或表述為：
若點O(x0,y0)在圓（x-a)^2+(y-b)^2=r^2上，
則過點P的切線方程為
(x-a)(x0-a)+(y-b)(y0-b)=r^2
證明：
（1）（向量法）
設圓上一點A為（x0,y0),則該點與圓心O的向量OA（x0-a,y0-b)
因為過該點的切線與該方向半徑垂直，則有切線方向上的單位向量與向量OA的點積為0.
設直線上任意點B為(x,y)
則對於直線方向上的向量AB（x-x0,y-y0)
有向量AB與OA的點積
AB●OA=(x-x0)(x0-a)+(y0-b)(y-y0)
=（x-a+a-x0)(x0-a)+(y0-b)(y-b+b-y0)
=(x-a)(x0-a)+(y-b)(y0-b)-(x0-a)^2-(y0-b)^2=0
故有(x-a)(x0-a)+(y-b)(y0-b)=(x0-a)^2+(y0-b)^2=r^2
（2）（分析-解析法）
設圓上一點A為（x0,y0),則有：(x0-a)^2+(y0-b)^2=r^2
對隱函式求導，則有：
2(x0-a)dx+2(y0-b)dy=0
dy/dx=(a-x0)/(y0-b)=k
（隱函式求導法亦可證明橢圓的切線方程，方法雷同）
或直接k1=(y0-b)/(x0-a); k*k1=-1;（k1為與切線垂直的半徑斜率。）
得k=(a-x0)/(y0-b) （以上處理是假設斜率存在，在後面討論斜率不存在的情況）
所以切線方程可寫為：y=(a-x0)/(y0-b)x+B
將點（x0,y0),可求出B=（x0-a)x0/(y0-b)+y0
所以:
y(y0-b)+(x0-a)x=(x0-a)x0+(y0-b)y0
(y0-b)(y-b+b-y0)+(x0-a)(x-a+a-x0)=0
(y0-b)(y-b)+(x0-a)(x-a)=(x0-a)^2+(y0-b)^2
(y0-b)(y-b)+(x0-a)(x-a)=R^2
當斜率不存在時，切點為與x軸平行的直線過圓心與圓的交點。
此類切點有2個，不妨設為M（a-r,b);N(a+r,b)
(y0-b)(y-b)+(x0-a)(x-a)=r^2
將2點帶入上式，亦成立。
故得證。
