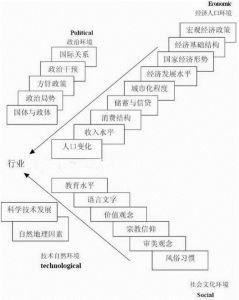
套用目的
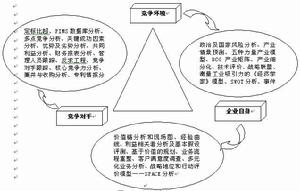 趨勢分析法
趨勢分析法運用方式
一重要財務指標的比較趨勢,預測其發展前景。這種方式在統計學上稱之為動態分析。它可以有兩種方法來進行。
1、定基動態比率:即用某一時期的數值作為固定的基期指標數值,將其他的各期數值與其對比來分析。其計算公式為:定基動態比率=分析期數值÷固定基期數值。例如:以2000年為固定基期,分析2001年、2002年利潤增長比率,假設某企業2000年的淨利潤為100萬元,2001年的淨利潤為120萬元,2002年的淨利潤為150萬元。則:
2001年的定基動態比率=120÷100=120%;2002年的定基動態比率=150÷100=150%
2、環比動態比率:它是以每一分析期的前期數值為基期數值而計算出來的動態比率,其計算公式為:環比動態比率=分析期數值÷前期數值。仍以上例資料舉例,則:2001年的環比動態比率=120÷100=120%;2002年的環比動態比率=150÷120=125%
二會計報表的比較
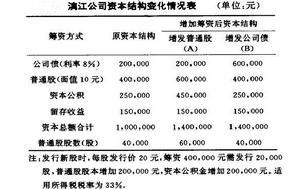 趨勢分析法
趨勢分析法會計報表的比較是將連續數期的會計報表金額並列起來,比較其相同指標的增減變動金額和幅度,據以判斷企業財務狀況和經營成果發展變化的一種方法。運用該方法進行比較分析時,最好是既計算有關指標增減變動的絕對值,又計算其增減變動的相對值。這樣可以有效地避免分析結果的片面性。例如:某企業利潤表中反映2000年的淨利潤為50萬元,2001年的淨利潤為100萬元,2002年的淨利潤為160萬元。
通過絕對值分析:2001年較2000年相比,淨利潤增長了100-50=50(萬元);2002年較2001年相比,淨利潤增長了160-100=60(萬元),說明2002年的效益增長好於2001年。而通過相對值分析:2001年較2000年相比淨利潤增長率為:(100-50)÷50×100%=100%;2002年較2001年相比淨利潤增長率為:(160-100)÷100×100%=60%。則說明2002年的效益增長明顯不及2001年。
三會計報表項目構成比較這種方式是在會計報表比較的基礎上發展而來的,它是以會計報表中的某個總體指標為100%,計算出其各組成項目占該總體指標的百分比,從而來比較各個項目百分比的增減變動,以此來判斷有關財務活動的變化趨勢。這種方式較前兩種更能準確地分析企業財務活動的發展趨勢。它既可用於同一企業不同時期財務狀況的縱向比較,又可用於不同企業之間的橫向比較。同時,這種方法還能消除不同時期(不同企業)之間業務規模差異的影響,有利於分析企業的耗費和盈利水平,但計算較為複雜。在採用趨勢分析法時,必須注意以下問題:1、用於進行對比的各個時期的指標,在計算口徑上必須一致;2、必須剔除偶發性項目的影響,使作為分析的數據能反映正常的經營狀況;3、套用例外原則,對某項有顯著變動的指標作重點分析,研究其生產的原因,以便採取對策,趨利避害。
總體分類
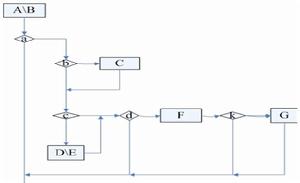 趨勢分析法
趨勢分析法趨勢分析
綜述
 趨勢分析法
趨勢分析法軌跡信號
Trigg's軌跡信號=修勻預測誤差(SFE)/平均絕對偏差(MAD)。與其有關的基本數學關係如下。通過指數修勻獲得的平均值估計值稱為修勻平均數(sm—mean)。在測定序列中每一次測定的sm—mean,由公式9—1進行計算:sm—mean=a×(新的一次控制測定值)+(1—a)×(前sm—mean)(9—1)式中a是修勻係數,由控制測定值個數(N)決定,a=2/(N+1),(0控制測定值由a加權,倒數第二個最近控制測定值由a(1—a)加權,倒數第三個最近控制測定值由。a(1—a)2加權,等等。若a為0.2,則最近的控制測定值的權數為0.2,按逆順序,前面的控制測定值的權數依次為0.16,0.128等等。
對於標準差可進行類似的計算,但其計算更加複雜,因為必須首先計算新的控制測定值與平均數估計值之間的差,而該差值則被稱為預測誤差。預測誤差=新的控制測定值一前sm—mean(9—2);修勻預測誤差(SFE)=a×(新的預測誤差)十(1—a)×(前修勻預測誤差)(9—3);預測誤差通過指數修勻計算處理得出精密度估計值,稱為平均絕對偏差(MAD,MeanAbsoluteDeviation)。MAD=a×(新的預測誤差)—(1—a)×(前MAD)(9—4)
最後可得:軌跡信號=修勻預測誤差(SFE)/平均絕對偏差(MAD))(9—5);一般把軌跡信號在95%和99%可信水平定為警告和失控的界限。不同N時軌跡信號的控制限
Na警告界限失控界限
50.330.710.82
100.200.610.80
150.100.410.54
200.100.410.54
平均數規則
 趨勢分析法
趨勢分析法此規則主要用於監測系統誤差,即是趨勢分析中“準確度趨勢分析”指示系統。在套用此規則時,最初開始計算修勻平均數(sm—mean)的“前sm—mean’,實際上即為質控物測定值的平均數(T—mean)。若最初質控物的標準差為Ts,則用此平均數規則評價質控狀態時,系由質控物的平均數檢驗修勻平均數的估計值,而以Z-值進行檢驗:Z=N(sm—mean—T—mean)/Ts(9—6)其中Z相當於標準差的個數,與統計檢驗“顯著性水平”有關。由Pfr確定的不同水平的Z值,即可根據公式9—6計算出Trigg's平均數規則中修勻平均數(sm—nlean)的控制限。
Na控制限
Pfr=0.01Pfr=0.002
50.331.25(Ts)1.38(Ts)
100.200.82(Ts)0.98(Ts)
150.100.67(Ts)0.79(Ts)
200.100.58(Ts)0.69(Ts)
方差卡方規則
 趨勢分析法
趨勢分析法此規則主要用於監測隨機誤差,即趨勢分析中“精密度趨勢分析”指示系統;其中最關鍵的統計量為修勻標準差sm—s,sm—s的數學表達式為:修勻標準差(9—7)式中的a和MAD在上面已定義。具體方法是:由卡方(X2)統計檢驗對修勻標準差(sm—s)估計值的顯著性變化進行檢驗,即將“真”方差(T2s)與修勻標準差的平方(sm2s)進行比較:X2=(sm2s/T2s)×(N-1)(9—8);由Pfr確定在不同水平的臨界卡方值(X2)並根據公式9—8計算的Trigg's方差卡方規則的控制限。
方差卡方規則的控制限
Na控制限
Pfr=0.05Pfr=0.01Pfr=0.002
50.331.54(Ts)1.82(Ts)2.15(Ts)
100.201.37(Ts)1.55(Ts)1.75(Ts)
150.101.30(Ts)1.44(Ts)1.61(Ts)
200.101.26(Ts)1.38(Ts)1.52(Ts)
銷售預測
算數平均法適用於每月銷售量波動不大的產品的銷售預測
加權平均法中的權數選取應該遵循“近大遠小”的原則
移動平均法適用於銷售量略有波動的產品預測
指數平滑法實質上是一種加權平均法
作用
通過趨勢分析可以知道企業財務經營的變化情況,為預測未來發展方向提供幫助。
經濟學大觀園
| 浩瀚無邊的書海中有著無窮無盡的精華,我們想要逐一去認知他們卻不是一件容易的事情。諸如經濟這種“高深莫測”的學科,更讓一般人望而生畏。 |