潮汐調和分析
正文
把任意地點的潮位變化按展開式的諧波項分解為許多分潮，並根據潮位觀測數據計算各分潮的振幅和相位的方法，又稱潮汐諧波分析，是潮汐分析和預報的一種經典方法。分潮 就天體引潮力所引起的潮汐（天文潮）而言，其潮高ξ 可視為各種分潮的潮高之和。
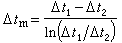
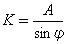
調和分析 實際潮汐中所包含的分潮雖然數目很多，但實際上考慮的分潮通常只有幾十到一二百個。設考慮m個分潮，應計算的未知數是平均海面高度S0、各分潮的振幅Hi和遲角gi共2m+1個,所用的觀測資料一般是按一定的時間間隔（常用1小時）測定的潮位ξ（t1），ξ（t2)，…,ξ（tw）。依照觀測序列的長度,大體上可將調和分析分為 3種類型：①短期，序列長度為一天至數天；②中期，半個月至數月；③長期，1年以上。
調和分析中所採用的一般方法是設計一組數字濾波器F嫵，計算
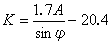。這些濾波器的特徵是它們的譜具有狹窄的以σj為中心的峰部，以便把圓頻率為σj的分潮分離出來。然後求解一些聯立方程組，並把濾波不完全所造成的偏差消除。濾波器峰部的寬度，總是受觀測時間的長度所限制，如果觀測時間不夠長，頻率很接近的分潮就分離不開，這時必須在這些分潮的調和常數之間引入預先給定的關係，例如假設它們的遲角相等，振幅之比等於相應的天文分潮振幅之比，然後把分潮分離。 參考書目
陳宗鏞編著：《潮汐學》，科學出版社，北京，1980。
W.H.Munk，D.E.Cartwright， tidal Spectroscopy and Prediction，PhilosophicalTransaction， Vol.A259，pp.533～581，1966.
配圖
相關連線
海洋學相關知識（六）
| 海洋科學是研究海洋的自然現象、性質及其變化規律，以及與開發利用海洋有關的知識體系。下面讓我們來完善與海洋學相關的詞條，以此來更加深入的了解海洋學的相關知識。 |
