正文
在日、月引潮力的作用下,固體地球產生的周期性形變的現象。月球和太陽對地球的引力不但可以引起地球表面流體的潮汐(如海潮和大氣潮),還能引起地球固體部分的周期性形變。由於其他天體距地球甚遠,對地球的引力甚微,在固體潮的研究中一般可略而不計。太陽的質量雖然是月球質量的2700萬倍,但月球同地球的距離只有太陽同地球距離的1/390,所以月球的引潮力為太陽引潮力的2.25倍。地球的固體部分並不是完全的剛體。地殼上層具有一定的剛性,地幔物質具有某種塑性,地核外層為液態(見地球內部的構造和物理性質)。固體潮使大地水準面的形狀發生周期性的變化,局部發生傾斜,面上的重力值也發生變化。引潮力使地球各部分發生形變,並引起地球密度的變化,由此產生附加的引力位。到目前為止,在引起固體地球形變的種種因素(例如冰雪和海水的負荷、大陸漂移、岩石層的構造運動,等等)中,還只有固體潮能從理論上預先計算出引起形變的作用力。由於對地球內部構造模式的改進,現在已有可能以相當高的精度估算出地麵點由於固體潮產生的形變數,從而可為精密大地測量工作提供地面變形的改正數據;在天文學中,可用於研究地球自轉、極移和歲差、章動等現象;在地球物理學中,可用於研究地球內部構造。
研究簡史 早在1876年,英國的開爾文(Kelvin)從地球形變的跡象中提出地球是彈性體而不是完全剛體的觀點。這種跡象主要表現為天文觀測中的一些偏差,但當時沒有觀測固體潮的手段,不能加以驗證。19世紀60年代,德國的策爾納 (J.K.F.Z╂llner)研製成功水平擺,並於80年代用於實際觀測。但由於受到當時觀測技術和理論研究水平的限制,其觀測數據仍不能用於驗證地球的彈性問題。一般認為最可能的驗證是利用海潮的觀測數據,但海潮是不遵守平衡潮規律的,所以,直到1883年英國的達爾文(G.H.Darwin)對海潮觀測中長周期分量的數據進行比較,發現它只有理論值的2/3,他認為所損失的1/3是由於地球的固體表面發生與海水類似的周期性漲落所致,從而驗證了固體潮的存在。20世紀50年代,隨著精密儀器的出現,特別是有了精密重力儀,固體潮的觀測和研究才有了實際的可能。1957年國際地球物理年期間,世界上開始了系統的固體潮觀測和研究工作。
理論 引潮力 作用在地球的單位質點上的日、月引力和地球繞地月(和地日)公共質心鏇轉所產生的慣性離心力的合力稱為引潮力。隨著作用點的位置不同和日、月相對於地球的位置變化,引潮力的大小和方向也發生改變。下圖表示在某一時刻地球上某一地點A所受到的月球引潮力的情況。圖中P為地球繞地月公共質心鏇轉的慣性離心力,F為月球的引力,G為月球的引潮力,在此影響下,A點移到A'的位置,整個地球由此引起的形變如圖中虛線所示。太陽對地球的引潮力也與此類似。 引潮力位 引潮力可以表示為一個標量函式的梯度,這個標量函式稱為引潮力位。由月球和太陽在地球內部形成的引潮力位既是隨時間變化的函式,也是作用點在地球內部位置的函式。和地球重力場的研究方法一樣,引潮力位也可以用球諧函式展開式來表示。若將坐標的原點放在地球的質心,則零階(或次)項對地球的形變不起作用,1階項等於零,3階項已很微小,只是在一些特殊問題上有時會用到,4階以上的項則因非常微小而忽略不計,一般討論只限於2階項。
如果把地球看作剛體,則引潮力引起的剛體地球表面上的重力變化,稱為重力固體潮的理論值。它是引潮力位對矢徑的導數,即: 式中塐為引潮力位。剛體地球表面上任一點的重力和某一瞬時的引潮力的合矢量方向隨時間不斷變化。這種變化表現為剛體地球表面的傾斜,這種傾斜稱為地傾斜固體潮的理論值。由於它具有方向性,通常用兩個分量來表示:南北分量ζ和東西分量η。它們分別由引潮力位對緯度嗘 和經度λ方向的導數求得,即:
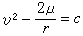
平衡潮 假設在剛體地球表面上覆蓋一層海水,海水是不可壓縮的,設其質量和運動的慣性力都可略而不計,於是海水面在每一瞬間都處於靜止平衡狀態。根據這種假定,海水面在重力和引潮力的作用下,其形狀相對於大地水準面將發生不斷的變化,稱為平衡潮。海水面沿徑向位移稱為平衡潮高ζ,它可以通過引潮力位求得,即:
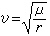
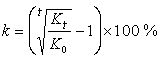 ,
,
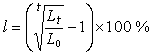 。
。
70年代中,美國史密斯(D.E.Smith)建立了鏇轉橢球的彈性地球模型,由於考慮到地球的扁率和科里奧利力,使問題變得複雜,但在理論上更加完善。1979年,他的學生瓦爾(J.Wahr)進一步完善了這一工作。瓦爾的貢獻在於提出了採用本徵函式求解的方法,並實際地解算了考慮到扁率和自轉的地球彈性形變方程,推出洛夫數h、k和l的理論值。
觀測 研究固體潮一方面必須在地面上進行大量的精密觀測,推算出洛夫數以及它們的分布規律,另一方面又可以根據已知的地球模型直接解算出洛夫數。通過實踐與理論的比較,可進一步闡明地球內部結構和物理性質。
數據推算 對於實際地球,固體潮所引起的變化除了剛體地球表面傾斜變化和重力變化的理論值外,還有地球彈性形變和附加引力位的影響。在兩者的聯合影響下所得觀測值與理論值之比稱為固體潮特徵數。重力觀測的特徵數以δ表示,它與洛夫數的關係為:
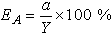 ,
,
γ=1+k-h ,
此特徵數永遠小於1,一般在0.6~0.7之間,故又稱為縮小特徵數。由此,地面上觀測到的固體潮引起的重力變化為:
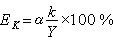 。
。
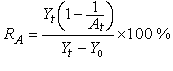
Λ=1+k-l。
固體潮引起地麵點的緯度和經度變化分別為: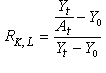
地面固體潮水平位移S嗗 和S懁可由下式表示:
 (南北分量),
(南北分量),
。
上述的觀測數據都可用精密的儀器進行測量。例如,重力變化可用高精度重力儀觀測。傾斜變化多用水平擺觀測。固體潮水平位移可用伸縮儀觀測。由於各種固體潮的數值甚微,且需要通過連續觀測才能獲得,所以觀測儀器必須具有很高的精度,能夠自動連續記錄觀測結果,同時還必須儘可能消除各種外界干擾因素。清除干擾 固體潮觀測所受到的最大的外界干擾因素來自海潮的影響,稱為間接效應。這種影響表現在3個方面:①海水質量所引起的引力變化;②在海潮的負荷作用下地殼產生的形變;③由於這種形變而產生的附加引力位。海潮和固體潮的產生都是由於日、月引力,其周期完全相同,因此採用一般的數學解算顯然無法把二者分開。如果準確知道海潮負荷的大小及其作用規律,則通過計算可把海潮影響從固體潮中扣除掉。為了解決這個問題,60年代以來,發展了負荷潮汐形變理論。它研究固體地球在地球表面負荷作用下的形變。朗曼(I.M.Longman)及隨後的法雷爾(W.E.Farrel,1972)認為,如果地球的表面負荷也同日、月引潮位一樣,用一組叫做負荷潮汐洛夫數k′、h′、l′的參數表示,可據此推導出全部計算公式。為此必須具有精確的海潮圖。海潮圖是一種繪有等潮線(即潮高相等的曲線)的圖,通常採用經驗方法或解算海潮拉普拉斯方程求得。但目前精度還較低,不同作者所假想的邊值條件不同,其結果也相差很大。1970年,美國的郭宗汾提出利用重力固體潮觀測反演海潮圖的方法。他的試驗是根據大陸和島嶼上進行的重力潮汐觀測加上海岸驗潮站的觀測,套用線性規劃求逆的方法,求出大洋的海潮圖,並把此圖與設在海底的驗潮站觀測結果相比較,以證明其方法有的效性。這一思想受到國際上的重視。郭宗汾對東北太平洋和北大西洋西部進行了試驗,收到了預期的效果。隨後比利時的梅爾基奧爾(P.Melchior)開始其環球的重力剖面測量,從歐洲開始,直到南太平洋,試圖以此來檢驗現有一些海潮圖在大西洋、北海、印度洋、南中國海和南太平洋的有效性。
數據處理 在固體潮的研究中,有兩方面的數據。一方面是實際觀測的數據,另一方面是理論計算的數據。它們都是引潮力位塐 的導數。引潮力位完全可根據公式精確地算出。所以,上述的理論數據也是可知的。實測數據(經過必要的修正)與相應的理論值之比,就是所要推求的特徵數δ或γ、或Λ等。引潮力位是月球和太陽的共同作用產生的,在理論值的計算中,常把月球和太陽分開來處理,並且將每個天體的計算公式分解成很多不同頻率的函式,所以任一時刻的引潮力位都可分解成很多不同頻率的分量之和。同樣,實際的觀測值也必須分解成不同頻率的分量,然後以相同頻率的實測值與理論值比較,由此求出特徵數。實測數據的分解,主要是套用調和分析方法,也就是套用濾波技術,將一段時間內的觀測數據序列按不同頻率的分量逐步地分離開來。
觀測值與理論值的差異有兩方面:一是振幅差,由此可求出特徵數δ、γ或Λ;另一是相位差,即所謂相位滯後。這些都是研究地球內部問題的重要數據。有了特徵數δ、γ或Λ,就可以求出洛夫數 k、h和l。顯然,這些洛夫數也是同頻率有關的。
研究成果的套用 由於受固體潮的影響,地面不停地變形,這就影響到各種測量數據的精確度。利用固體潮的理論則可以對這些精密測量結果加以改正。例如:
①絕對重力測量值是一種計量標準,精密的重複相對重力測量則是研究地殼形變的重要手段,現在重力觀測的精度已達到10~20微伽的量級,而重力潮汐變化影響的最大幅度可達±130微伽。因此,在精密的重力測量中須加以改正。
②雷射測距和測月技術的發展,已使測距精度達到幾至十幾厘米。而地面測站的垂直潮汐形變要達到30~40厘米的幅度,因此必須加以改正。對於雷射測月來說,除去地球表面測站外,月面上的反射鏡站也將因月潮產生形變,而且由於地球質量比月球質量大得多,這一形變數將遠超過地球表面。
③衛星大地測量的發展,已可能利用安置在衛星上的雷達測高儀,測定海洋上的大地水準面差距來反求海洋面上的重力異常,測高儀的精度可達0.1~0.5米。因此,在考慮測高瞬時海洋潮汐的影響時,也應顧及固體潮對海潮的影響。
④除地球引力場、日月引力及大氣阻力外,固體潮的變化對衛星的軌道也有攝動作用,所以在衛星的軌道設計中必須顧及這一影響。
長期以來,人們就知道地球的自轉是不斷減慢的。古生物學家對珊瑚年輪的研究表明,日長是不斷增加的,例如在距今約4.25億年的志留紀,每年有407天,即那時1天的長度只合現在的21.5小時,而在2.8億年前的二疊紀則為22.8小時,平均計算每10萬年日長增加2秒。從古代歷史的日食記載及近 200年日食觀測所推算的結果與此大致相同。
固體潮研究與日長的長期變化有密切關係。固體地球是一個滯彈性體,因此固體地球對引潮力的回響將有一個滯遲。例如,當天體(月球或太陽)在中天時刻,並不就是出現高潮的時刻。因為固體地球的粘滯性將使得它在受引潮力作用而起潮時受到潮汐摩擦,從而使潮汐的起落落後於引潮力的變化。由於固體潮汐摩擦所消耗的能量比率與地球的相位滯后角(可以從近代精密的重力潮汐觀測中求出)成正比,從而可推得地球自轉長期減慢的量級。據梅爾基奧爾從受海潮間接影響較小的潮波的觀測結果得出,滯后角約為1°左右,這樣就使每10萬年日長增加2秒。帕里斯基(П.Парийский)經過對最新海潮圖的改正得出的結果為每 10萬年日長增加3.8秒。
地球在引潮力作用下的彈性形變,造成地球內部質量的重新分布和地球主慣性矩的變化。這個變化量同代表附加位變化的洛夫數k有關,並且主要來自引潮力位中的長周期項,從而使地球自轉速度伴隨有周期性的變化。其中對於18.6年周期,幅度可達154.5毫秒;對於半年周期,幅度為4.6毫秒;而1年周期的幅度為1.5毫秒。這些數值在天文測時精度日益提高的今天,已經能夠觀測出來。因此,一方面在測時結果中應顧及和消去這種周期性影響,另一方面又可從長期的測時結果中反求出洛夫數k值。
固體潮和天文學之間的一個重要聯繫是關於地球自轉軸在慣性空間運動的問題,即歲差、章動現象。它和全日潮都是由同一個外力矩產生的。但因為章動是地球自轉軸在一慣性系統中的運動,固體潮則是在固定於地球上的測站上觀測的,地球以角速度ω=15.041度/小時鏇轉,所以,天文章動的頻率和全日潮頻率要差一個“恆星頻率”。據此,全日潮中頻率ω=15.041度/小時的K1波就相當於章動頻率為零的長期項,即天文上50.2″的歲差,頻率與K1波頻率相對稱的一對潮波,就產生天文章動項,其振幅完全可由引潮力位展開的振幅算出,這樣,固體潮中的全日潮波展開項和天文章動項可以一一對應起來。
從天體力學角度探索章動問題,主要分量有18.6年周期、幅度為9.22″的長期項,0.55″的半年項,以及0.09″的半月項等。按現代天文測量的精度,半月項就很難由觀測數據中分析出來,但與此相對應的潮波則有可能從重力儀和傾斜儀分辨出來。因為這些儀器都具有能連續觀測和高精度的優點。
近幾十年來,人們還企圖從固體潮方面來研究地球核的物理狀態問題。因為對於給定的一種地球內部模型,從理論上可算出地面上應觀測到的洛夫數k、h、l,不同的地球模型可以有不同的洛夫數。這種從理論模型推算出的值同實際地面觀測的值相比較,就可以鑑別所假設的地球模型是否符合實際。現在從固體潮研究中可以得出如下的結論,即由地核的μ=0或μ=0.6×10-12 所推得的洛夫數與實際較為接近,由此可見,地核完全有可能接近液態。
參考書目
方俊:《固體潮》,科學出版社,北京,1984。
