定義
設集合X上有一全序關係,如果我們把這種關係用 ≤ 表述,則下列陳述對於 X 中的所有 a, b 和 c 成立:
如果 a ≤ b 且 b ≤ a 則 a = b (反對稱性)
如果 a ≤ b 且 b ≤ c 則 a ≤ c (傳遞性)
a ≤ b 或 b ≤ a (完全性)
配對了在其上相關的全序的集合叫做 全序集合(totally ordered set)、 線序集合(linearly ordered set)、 簡單序集合(simply ordered set)或 鏈(chain)。 鏈還常用來描述某個偏序的全序子集,比如在佐恩引理中。
關係的完全性可以如下這樣描述:對於集合中的任何一對元素,在這個關係下都是 相互可比較的。
注意完全性條件蘊涵了自反性,也就是說, a ≤ a。因此全序也是偏序(自反的、反對稱的和傳遞的二元關係)。全序也可以定義為“全部”的偏序,就是滿足“完全性”條件的偏序。
可作為選擇的,可以定義全序集合為特殊種類的格,它對於集合中的所有 a, b 有如下性質:
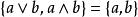 全序關係
全序關係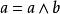 全序關係
全序關係我們規定 a ≤ b 若且唯若。可以證明全序集合是分配格。
全序集合形成了偏序集合的範疇的全子範疇,通過是關於這些次序的映射的態射,比如,映射 f 使得"如果 a ≤ b 則 f(a) ≤ f(b)"。
在兩個全序集合間的關於兩個次序的雙射是在這個範疇內的同構。
嚴格全序
對於每個(非嚴格)全序 ≤ 都有一個相關聯的非對稱(因此反自反)的叫做 嚴格全序的關係 <,它可以等價地以兩種方式定義:
•a < b 若且唯若 a ≤ b 且 a ≠ b
•a < b 若且唯若 ¬(b ≤ a) (就是說 > 是 ≤ 的補關係的逆關係)
性質:
•關係是傳遞的: a < b 且 b < c 蘊涵 a < c。
•關係是三分的: a < b, b < a 和 a = b 中有且只有一個是真的。
•關係是嚴格弱序,這裡關聯的等價是等同性。
我們可以其他方式工作,選擇 < 為三分的二元關係;則全序 ≤ 可等價地以兩種方式來定義:
•a ≤ b 若且唯若 a < b 或 a = b
•a ≤ b 若且唯若 ¬(b < a)
還有兩個關聯的次序是補關係 ≥ 和 >,它們構成了四元組 {<, >, ≤, ≥}。
我們可以通過這四個關係中的任何一個,定義或解釋集合全序的方式;由符號易知所談論的是非嚴格的,抑或是嚴格全序。
全序關係與偏序關係
偏序和全序是公里集合論中的概念。首先需要知道什麼是二元關係。比如實數中的“大小”關係,集合的集合中的“包含”關係就是兩種二元關係。所謂偏序,即偏序關係,是一種二元關係。所謂全序,即全序關係,自然也是一種二元關係。全序是指,集合中的任兩個元素之間都可以比較的關係。比如實數中的任兩個數都可以比較大小,那么“大小”就是實數集的一個全序關係。偏序是指,集合中只有部分元素之間可以比較的關係。比如複數集中並不是所有的數都可以比較大小,那么“大小”就是複數集的一個偏序關係。顯然,全序關係必是偏序關係。反之不成立。
例子
•字母表的字母按標準字典次序排序,比如 A < B < C 等等。
•把一個全序限制到其全序集合的一個子集上。
•所有的兩個元素都是可比較的任何偏序集合 X (就是說,如果 a,b 是 X 的成員,則 a≤b 或 b≤a 中的一個為真或二者都為真)。
•由基數或序數(實際上是良序)組成的任何集合。
•如果 X 是任何集合,而 f 是從 X 到一個全序集合的單射函式,則 f 誘導出 X 上的一個全序:規定 x < x 若且唯若 f(x) < f(x)。
•設有某個集族,其成員都是用序數為索引的全序集合,然後把這集族上取的笛卡爾積中的有序對按字典序排序,那麽,這字典序是一全序。例如,若有一個集合由一些詞語組成,按字母表把詞語排序的話會是一全序。舉個實例,我們規定"bird"先於"cat"。這可視為是向字母表加入空格符號""(定義""先於所有字母),得到集合A,然後對其自身取可數次笛卡爾積,得到A。"bird"可理解為A里的序對("b","i","r","d","","",...),"cat"則是("c","a","t","","","",...)。從而{"bird","cat"}成為A的一個子集,把A上的字典序限制到這字集,便得出"bird"<"cat"。
•實數集和自然數集、整數集、有理數集(作為實數集的子集),用平常的小於(<)或大於(>)關係排序都是(嚴格)全序的。它們都可以被證明是帶有特定性質的全序集合的唯一的(在同構意義下的)最小實例(一個全序 A 被稱為是帶有特定性質的最小全序,即意味著只要別的全序 B 有這個性質,就有從 A 到 B 的子集的一個序同構):
•自然數集是最小的沒有上界的全序集合。
•整數集是最小的沒有上界也沒有下界的全序集合。
•有理數集是最小的在實數集內稠密的全序集合,這裡的稠密性是指對於任意實數a, b,都存在有理數q使得a
•實數集是最小的無界連通(序拓撲的意義下)的全序集合。