性質
雙重非負性
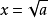算術平方根在
中a
1.a≥0（若小於0，則為虛數）
2.x≥0
與平方根的關係
正數的平方根有兩個，它們為相反數，其中正的平方根，就是這個數的算術平方根。
產生
根號（即算術平方根）的產生源於正方形的對角線長度“根號二”，這個 “根號二”的發現 一度引起了畢達哥拉斯學派的恐慌。因為按當時的權威解釋（也就是畢達哥拉斯學派的學說），萬物皆數（也就是說世界上所有的事物都可以用數來表示）
對於這個無理數“根號二”，最終人們選取了用根號來表示。
舉例
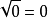算術平方根9的平方根為±3 ；9的算術平方根為3，正數的平方根都是前面加±，算術平方根全部都是非負數（0也在內，
）
辨析
算術平方根和平方根是大家學習實數接觸最多的概念，兩者密不可分。可對於初學者來說是對“孿生殺手”，很容易在解題過程中產生錯誤。算術平方根和平方根到底有哪些區別與聯繫呢？
區別
1、定義不同：
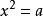算術平方根⑴絕大部分地，如果一個正數x的平方等於a，即
，那么這個正數x叫做a的算術平方根（arithmetic square root）。
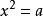算術平方根⑵一般地，如果一個數的平方等於a，那么這個數叫做a的平方根或二次方根（square root）。這就是說， 如果
，那么x叫做a的平方根。
2、表示方法不同：
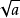算術平方根⑴a的算術平方根記為
，讀作“根號a”，a叫做被開方數（radicand）。
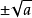算術平方根⑵a的平方根記為
，讀作“正負根號a”，其中a叫做被開方數。
3、個數不同：從形式上看，二者的符號主體相似，但是一個數的平方根要在其算術平方根的前面寫上“±”。這也正好說明了一個正數和零的算術平方根有且只有一個，而一個正數卻有兩個互為相反數的平方根。零隻有一個平方根。
聯繫
1、前提條件相同：算術平方根和平方根存在的前提條件都是“只有非負數才有算術平方根和平方根”。
2、存在包容關係：平方根包含了算術平方根，因為一個正數的算術平方根只是其兩個平方根中的一個。
3、0的算術平方根和平方根相同，都是0。
輸入方法
電腦上輸出方法
根號的打法有以下幾點：
比較通用：左手按住換檔鍵（Alt鍵）不放，接著依次按41420（鍵盤右方的數字鍵區）然後鬆開左手，根號“√”就出來了。
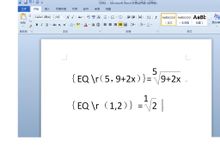在Word中輸入根號運用Word的域命令在Word中根號：首先按住Ctrl+F9，出現{}後，在{}內輸入EQ空格\r（開方次數，根號內的表達式），最後按住Shift+F9，就會生成你所要求的根式
。
1.平方根
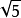算術平方根一個正數的平方根有兩個，它們互為相反數。比如 9 的平方根是3和-3。而5的平方根是
和
。規定，零的平方根是0。負數沒有實數平方根。
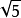算術平方根2.算術平方根是指一個正數的正的平方根。比如 9 的算術平方根是3。而5的算術平方根是
。規定,零的算術平方根是0。
算術平方根是定義在平方根基礎上，因此負數沒有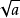算術平方根。
算術平方根3.實數a的算術平方根記作
，其中a≥0。根據以上定義有
。
