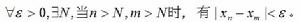總述
總述:
歷史車輪的轉離不開數學的發展。十七世紀,微積分這一銳利無比的數學工具為牛頓、萊布尼茨各自獨立發現,推動了科學技術的前進。然而,貝克萊對牛頓理論的攻擊,將無窮小量嘲笑為“消失的量的靈魂”,卻真正抓住了牛頓理論的缺陷。一方面,微積分在套用中大獲成功;一方面其自身卻存在著邏輯矛盾。至十九世紀,由十七、十八世紀積累下來的矛盾到了非解決不可的程度。
使分析基礎嚴密化的工作由法國著名數學家柯西邁出了第一大步。他給出了分析學一系列基本概念的嚴格定義。1823年,柯西給出了“柯西收斂定理”。而早在1817年,波爾察諾就確切地陳述了有界實數集的最小上界(即上確界)的定義。利用他的思想,魏爾斯特拉斯在19世紀60年代證明了“波爾察諾—魏爾斯特拉斯緊緻性定理”。海涅於1872年提出,波萊爾於1895年完善並證明了“有限覆蓋定理”。1872年,實數的三大派理論:戴德金“分劃”理論,康托的“基本序列”理論及魏爾斯特拉斯的“有界單調序列”理論,同時在德國出現了! 1892年,巴赫曼提出了建立實數理論的一個重要原理——區間套原理。由此,沿柯西開闢的道路建立起來的嚴謹的極限理論與實數理論,完成了分析學的邏輯奠基工作,從而使微積分學這座數學史上空前雄偉的大廈建在了牢固可靠的基礎之上。
主要內容
七個等價命題:
實數基本定理:對R的每一個分劃A|B,都存在唯一的實數r,使它大於或等於下類A中的每一個實數,小於或等於上類B中的每一個實數。
確界定理:在實數系R內,非空的有上(下)界的數集必有上(下)確界存在。
單調有界原理:若數列{Xn}單調上升有上界,則 {Xn}必有極限。
區間套定理:設{[a,b] }是一個區間套,則必存在唯一的實數r,使得r包含在所有的區間裡,即

有限覆蓋定理:實數閉區間[a,b]的任一覆蓋E,必存在有限的子覆蓋。
緊緻性定理:有界數列必有收斂子數列
柯西收斂定理:在實數系中,數列有極限存在的充分必要條件是: