歷史
在17世紀微積分學的初創時期,人們就注意到這門學科的基礎問題。I.牛頓和萊布尼茨都曾使用過無窮小,尤其是萊布尼茨及其跟隨者,在一階和高階無窮小的基礎上,發展了微積分理論;他們完全允許引進無窮小和無窮大,而且把它們看做是類似於虛數的理想元素,這些理想元素服從於普通實數的定律。他們所用的記號,在歐洲大陸上被廣泛採用。這些記號的優越性,促進了當時微積分理論在歐洲大陸上迅速發展。因此,魯賓孫把萊布尼茨視為非標準分析的真正先驅者。但是這個理論卻存在著顯著的內在矛盾──有時把無窮小看作非零而作除數,有時又把它看作是零而捨去。局限於當時的條件,這個矛盾一時還不能徹底解決,難免受到非難和攻擊。英國的主觀唯心主義哲學家B.貝克萊(1685~1753)主教在1734年著文攻擊無窮小為“消失了的量的幽靈”。直到19世紀,A.-L.柯西、B.波爾查諾和K.(T.W.)外爾斯特拉斯用極限理論為數學分析建立了邏輯上嚴謹的基礎,從而促進了數學分析的大發展。
此後,無窮小和無窮大在分析學中就再也沒有地位,只剩下了諸如“某變數趨於無窮大”這一類的說法而已。極限理論雖然使得數學分析獲得了邏輯的嚴謹性,但是卻失去了無窮小方法的簡明性和直觀性。正因為無窮小方法便於縮短論證,“更合於發明家的藝術”。許多物理學家、經濟學家和工程師仍習慣於運用無窮小方法。然而,數學家們卻認為在數學分析中作為數的無窮小是不存在的。直到20世紀60年代,魯賓孫運用數理邏輯嚴謹地論證了無窮小的存在性,圓滿地解決了萊布尼茨的“無窮小的矛盾”的問題,開創了非標準分析。接著W.盧森堡用超冪方法構造了非標準模型,以後又構造了多飽和模型。此後,非標準分析發展很快,現已成功地套用到許多方面,如點集、拓撲學、測度論、函式空間、機率論、微分方程、代數數論、流體力學、量子力學、理論物理和數理經濟等。非標準分析為具有眾多的小額貿易的商業市場提供了一個很好的模型。還有,它對模擬一個在邊界為無窮大的容器中的壓力下進行氣體的熱力學過程是很有成效的。非標準分析對某些學科中出現的一些困難問題已經作出有益的貢獻。例如,用非標準分析方法首先解決了幾十年未解決的希爾伯特空間上的多項式緊運算元的不變子空間的存在問題;又如,中國數學家用非標準分析方法給出了解決廣義函式的乘法問題的一個富有成效的方法;再如,法國數學家對常微分方程的奇異攝動已做出了大量很有意義的成果。還須指出,除非標準分析外,使得無窮小與無窮大能在分析學中使用的還有種種嘗試。在這方面最有成效的有D.勞格維茨的無窮小數和中國學者提出的廣義數的研究 。
定義
 超實數
超實數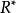 超實數
超實數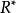 超實數
超實數 超實數
超實數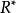 超實數
超實數 超實數
超實數 超實數
超實數 超實數
超實數 超實數
超實數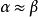 超實數
超實數 超實數
超實數 超實數
超實數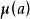 超實數
超實數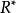 超實數
超實數 超實數
超實數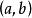 超實數
超實數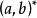 超實數
超實數 超實數
超實數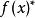 超實數
超實數 超實數
超實數 超實數
超實數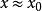 超實數
超實數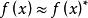 超實數
超實數 超實數
超實數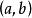 超實數
超實數 超實數
超實數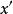 超實數
超實數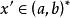 超實數
超實數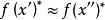 超實數
超實數美國數理邏輯學家A.魯賓遜於1960年創立。魯賓遜證明,實數結構 可擴張為包含無窮小數和無窮大數的結構 ,在一定意義下 與 有相同的性質。稱 中的數為超實數,形象地說,是在普通實數中又加進了無窮小數(其絕對值小於任何實數)及無窮大數(其絕對值大於任何實數)。當兩個超實數 與 相差為無窮小時,就稱 無限接近於 ,記為 ,這是一個等價關係。每個關於這個等價關係的等價類包含唯一的標準實數 。稱 所在的等價類 為一個單子,單子不是 中的數,而相當於 中的數,超實數可以進行四則運算,滿足通常的運算規律,也可以有大小順序。由此標準分析里的許多概念、定理等可以自然地擴張到非標準分析中。如區間 擴張為 , 中的函式擴張為 ,函式 在標準點 連續可定義為 時, ;函式 在 上一致連續可定義為當 , , 時 。
簡介
 超實數
超實數超實數系統是為了嚴格處理無窮量(無窮大量和無窮小量)而提出的。自從微積分的發明以來,數學家、科學家和工程師等(包括牛頓和萊布尼茲在內)就一直廣泛地用無窮小量等概念。超實數集,或稱為 非標準實數集,記為 ,是實數集 ℝ 的一個擴張;其中含有一種數,它們大於所有如下形式的數:
 超實數
超實數這可以解釋為 無窮大;而它們的倒數就作為 無窮小量。ℝ 滿足如下性質:任何關於 ℝ 的一階命題如果成立,則對 ℝ 也成立。這種性質稱為傳達原理。舉例來說,實數集的加法交換律
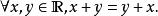 超實數
超實數是關於 ℝ 的一階命題。因此以下命題同樣成立:
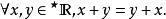 超實數
超實數也就是說超實數集同樣滿足加法交換律。
無窮小量的概念是否嚴格呢?此問題可以追溯到古希臘數學:數學家們如歐幾里得、阿基米德等,為了在一些證明里繞開無窮小量的爭議以保證嚴格性,而採用了窮竭法等其它說明方式。而亞伯拉罕·魯濱遜在1960年代證明了,
超實數系統是相容的,若且唯若實數系統是相容的 。
換句話說,如果對實數的使用沒有懷疑,那也可以放心使用超實數。在處理數學分析的問題時對超實數、尤其是傳達原理的使用,通稱為非標準分析。
