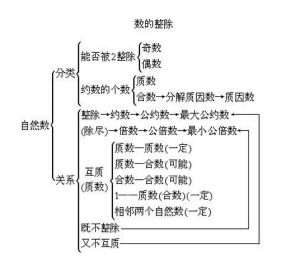
概述
自然數是指表示物體個數的數,即由0開始,0,1,2,3,4,……一個接一個,組成一個無窮的集體,即指非負整數。
數學術語
自然數集是全體非負整數組成的集合,常用N來表示。自然數有無窮無盡的個數。
【拼音】zì rán shù
【英譯】natural number
一般概念
自然數是一切等價有限集合共同特徵的標記。
註:整數包括自然數,所以自然數一定是整數,且一定是非負整數。
但相減和相除的結果未必都是自然數,所以減法和除法運算在自然數集中並不總是成立的。用以計量事物的件數或表示事物次序的數。即用數碼0,1,2,3,4,……所表示的數。表示物體個數的數叫自然數,自然數一個接一個,組成一個無窮集體。自然數集有加法和乘法運算,兩個自然數相加或相乘的結果仍為自然數,也可以作減法或除法,但相減和相除的結果未必都是自然數,所以減法和除法運算在自然數集中並不是總能成立的。自然數是人們認識的所有數中最基本的一類,為了使數的系統有嚴密的邏輯基礎,19世紀的數學家建立了自然數的兩種等價的理論:自然數的序數理論和基數理論,使自然數的概念、運算和有關性質得到嚴格的論述。
(序數理論是義大利數學家G.皮亞諾提出來的。他總結了自然數的性質,用公理法給出自然數的如下定義)
自然數集N是指滿足以下條件的集合:
①N中有一個元素,記作1。
②N中每一個元素都能在N中找到一個元素作為它的後繼者。
③1是0的後繼者。
④0不是任何元素的後繼者。
⑤不同元素有不同的後繼者。
⑥(歸納公理)N的任一子集M,如果1∈M,並且只要x在M中就能推出x的後繼者也在M中,那么M=N。
基數理論則把自然數定義為有限集的基數,這種理論提出,兩個可以在元素之間建立一一對應關係的有限集具有共同的數量特徵,這一特徵叫做基數。這樣,所有單元素集{x},{y},{a},{b}等具有同一基數,記作1。類似,凡能與兩個手指頭建立一一對應的集合,它們的基數相同,記作2,等等。自然數的加法、乘法運算可以在序數或基數理論中給出定義,並且兩種理論下的運算是一致的。
自然數在日常生活中起了很大的作用,人們廣泛使用自然數。自然數是人類歷史上最早出現的數,自然數在計數和測量中有著廣泛的套用。人們還常常用自然數來給事物標號或排序,如城市的公共汽車路線,門牌號碼,郵政編碼等。
自然數是整數(自然數包括正整數和零),但整數不全是自然數,例如:-1-2-3......是整數而不是自然數。自然數是無限的。
 自然數
自然數全體非負整數組成的集合稱為非負整數集,即自然數集。
在數物體的時候,數出的1.2.3.4.5.6.7.8.9……叫自然數。自然數有數量、次序兩層含義,分為基數、序數。
基本單位:計數單位:個、十、百、千、萬、十萬......
總之,自然數就是指大於等於0的整數。當然,負數、小數、分數等就不算在其內了。
嚴格定義
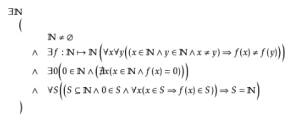 自然數
自然數右圖這個命題被稱為皮亞諾算術公理,該公理聲明了自然數集IN的存在性。
其中,第二條中聲明的單射f被稱為後繼映射,是我們生活中所習慣的“+1”。
第三條則聲稱,存在一個數是自然數的起始點,它不是任何數的後繼。
第四條則是我們所熟知的歸納假設,它使得在自然數集中數學歸納法的成立,也是對自然數集形態的一種限定。因為即使是有限集,也存在環形映射滿足第二條(自單射),任何無限集都滿足第二和第三條,而只有自然數集才能滿足所有這四條的限定。
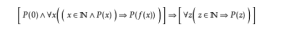 自然數
自然數由第四條,我們就可以使用數學歸納法如右圖,來證明自然數集中有關的命題。
性質
1、對自然數可以定義加法和乘法。其中,加法運算“+”定義為:
a+0=a;
a+S(x)=S(a+x),其中,S(x)表示x的後繼者。
如果我們將S(0)定義為符號“1”,那么b+1=b+S(0)=S(b+0)=S(b),即,“+1”運算可求得任意自然數的後繼者。
同理,乘法運算“×”定義為:
a×0=0;
a×S(b)=a×b+a
自然數的減法和除法可以由類似加法和乘法的逆的方式定義。
2、有序性。自然數的有序性是指,自然數可以從0開始,不重複也不遺漏地排成一個數列:0,1,2,3,…這個數列叫自然數列。一個集合的元素如果能與自然數列或者自然數列的一部分建立一一對應,我們就說這個集合是可數的,否則就說它是不可數的。
3、無限性。自然數集是一個無窮集合,自然數列可以無止境地寫下去。
對於無限集合來說“,元素個數”的概念已經不適用,用數個數的方法比較集合元素的多少只適用於有限集合。為了比較兩個無限集合的元素的多少,集合論的創立者德國數學家康托爾引入了一一對應的方法。這一方法對於有限集合顯然是適用的,21世紀把它推廣到無限集合,即如果兩個無限集合的元素之間能建立一個一一對應,我們就認為這兩個集合的元素是同樣多的。對於無限集合,我們不再說它們的元素個數相同,而說這兩個集合的基數相同,或者說,這兩個集合等勢。與有限集對比,無限集有一些特殊的性質,其一是它可以與自己的真子集建立一一對應,例如:
0,1,2,3,4…
1,3,5,7,9…
這就是說,這兩個集合有同樣多的元素,或者說,它們是等勢的。大數學家希爾伯特曾用一個有趣的例子來說明自然數的無限性:如果一個旅館只有有限個房間,當它的房間都住滿了時,再來一個旅客,經理就無法讓他入住了。但如果這個旅館有無數個房間,也都住滿了,經理卻仍可以安排這位旅客:他把1號房間的旅客換到2號房間,把2號房間的旅客換到3號房間,……如此繼續下去,就把1號房間騰出來了。
4、傳遞性:設n1,n2,n3都是自然數,若n1>n2,n2>n3,那么n1>n3。
5、三岐性:對於任意兩個自然數n1,n2,有且只有下列三種關係之一:n1>n2,n1=n2或n1<n2。
6、最小數原理:自然數集合的任一非空子集中必有最小的數。具備性質3、4的數集稱為線性序集。容易看出,有理數集、實數集都是線性序集。但是這兩個數集都不具備性質5,例如所有形如nm(m>n,m,n都是自然數)的數組成的集合是有理數集的非空子集,這個集合就沒有最小數;開區間(0,1)是實數集合的非空子集,它也沒有最小數。
具備性質5的集合稱為良序集,自然數集合就是一種良序集。容易看出,加入0之後的自然數集仍然具備上述性質3、4、5,就是說,仍然是線性序集和良序集。
分類
按是否是偶數分
可分為奇數和偶數。
1、奇數:不能被2整除的數叫奇數。
2、偶數:能被2整除的數叫偶數。也就是說,除了奇數,就是偶數。
註:0是偶數。(2002年國際數學協會規定,零為偶數。我國2004年也規定零為偶數。偶數可以被2整除,0照樣可以,只不過得數依然是0而已)。
按因數個數分
可分為質數、合數、1和0。
1、質數:只有1和它本身這兩個因數的自然數叫做質數。也稱作素數。
2、合數:除了1和它本身還有其它的因數的自然數叫做合數。
3、1:只有1個因數。它既不是質數也不是合數。
4、當然0不能計算因數,和1一樣,也不是質數也不是合數。
備註:這裡是因數不是約數。
數列
數列0,1,2,3,4,5,6,7,8,9,10,11,12,……n,稱為自然數列。
自然數列的通項公式an=n。
自然數列的前n項和Sn=n(n+1)/2。Sn=na1+n(n-1)/2。
自然數列本質上是一個等差數列,首項a1=1,公差d=1。
關於0
0的爭議
對於“0”,它是否包括在自然數之記憶體在爭議,有人認為自然數為正整數,即從1開始算起;而也有人認為自然數為非負整數,即從0開始算起。到21世紀關於這個問題也尚無一致意見。
在國外,有些國家的教科書是把0也算作自然數的。這本是一種人為的規定,我國為了推行國際標準化組織(ISO)制定的國際標準,定義自然數集包含元素0,也是為了早日和國際接軌。
現行九年義務教育教科書和高級中學教科書(試驗修訂本)都把非負整數集叫做自然數集,記作N,而正整數集記作N+或N*。這就一改以往0不是自然數的說法,明確指出0也是自然數集的一個元素。0同時也是有理數,也是非負數和非正數。
0的來由
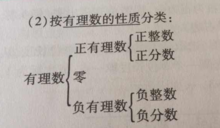 自然數
自然數直至約公元15,16世紀0和負數才逐漸給西方人所認同,才使西方數學有快速發展。0的另一個歷史:0的發現始於印度。公元左右,印度最古老的文獻《吠陀》已有“0”這個符號的套用,當時的0在印度表示無(空)的位置。約在6世紀初,印度開始使用命位記數法。7世紀初印度大數學家葛拉夫.瑪格蒲達首先說明了0的0是0,任何數加上0或減去0得任何數。遺憾的是,他並沒有提到以命位記數法來進行計算的實例。也有的學者認為,0的概念之所以在印度產生並得以發展,是因為印度佛教中存在著“絕對無”這一哲學思想。公元733年,印度一位天文學家在訪問現伊拉克首都巴格達期間,將印度的這種記數法介紹給了阿拉伯人,因為這種方法簡便易行,不久就取代了在此之前的阿拉伯數字。這套記數法後來又傳入西歐。
0的性質
0既不是正數也不是負數,而是正數和負數之間的一個數。當某個數X大於0(即X>0)時,稱為正數;反之,當X小於0(即X<0)時,稱為負數;而這個數X等於0時,這個數就是0。
0既不是正數也不是負數,而是介於-1和+1之間的整數。
0是偶數。
0是最小的完全平方數。
0的相反數是0,即,-0=0。
0的絕對值是其本身,即,∣0∣=0。
0乘任何實數都等於0,除以任何非零實數都等於0,任何實數加上0等於其本身。
0沒有倒數和負倒數,一個非0的數除以0在實數範圍內無意義。
0的正數次方等於0,0的負數次方無意義,因為0沒有倒數。
除0外,任何數的的0次方等於1。
0的0次方是懸而未決的,在某些領域定義為1,某些領域未定義。不定義的理由是以連續性為考量,不定義不連續點。
0不能做對數的底數和真數。
0也不能做除數、分數的分母、比的後項。
0在多位數中起占位作用,如108中的0表示十位上沒有,切不可寫作18。
0不可作為多位數的最高位。
當0不位於其他數字之前時表示一個有效數字。
0的階乘等於1。
0始終是直角坐標系的原點。
0是正數和負數的分界點。
任何數乘0都得0。
0是最小的自然數。
分式中分母為0無意義。
在複數集中,0是模最小的數,而且是唯一一個無輻角定義的元素。
低階無窮小與高階無窮小的比值是0。
定積分中,積分上限和下限相等時,積分值始終為0。
機率論中,用0表示不可能事件,或者在連續機率分布中位於某一特定自變數這一事件的機率。
套用
1、自然數列在“數列”,有著最廣泛的運用,因為所有的數列中,各項的序號都組成自然數列。
任何數列的通項公式都可以看作:數列各項的數與它的序號之間固定的數量關係。
2、求n條射線可以組成多少個角時,套用了自然數列的前n項和公式。
第1條射線和其它射線組成(n-1)個角,第2條射線跟餘下的其它射線組成(n-2)個角,依此類推得到式子:
1+2+3+4+……+n-1=n(n-1)/2
3、求直線上有n個點,組成多少條線段時,也套用了自然數列的前n項和公式。
第1個點和其它點組成(n-1)條線段,第2個點跟餘下的其它點組成(n-2)條線段,依此類推同樣可以得到式子:
1+2+3+4+……+n-1=n(n-1)/2
任何一自然數,可代入下公式,等式始終成立:
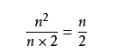 自然數
自然數