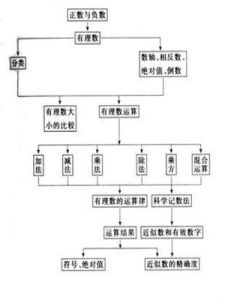
基本概況
整數和分數的統稱。正整數和正分數合稱為正有理數，負整數和負分數合稱為負有理數。因而有理數集的數可分為正有理數、負有理數和零3種數。由於任何一個整數或分
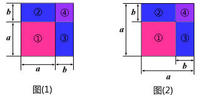有理數數形結合數都可以化為十進循環小數，反之，每一個十進循環小數也能化為整數或分數，因此，有理數也可以定義為十進循環小數。有理數集是整數集的擴張。在有理數集內，加法、減法、乘法、除法（除數不為零）4種運算通行無阻。有理數的大小順序的規定：如果a-b是正有理數，就稱a大於b或b小於a，記作a＞b或b＜a。任何兩個不相等的有理數都可以比較大小。有理數集與整數集的一個重要區別是，有理數集是稠密的，而整數集不是稠密的。將有理數依大小順序排定後，任何兩個有理數之間必定還存在其他的有理數，這就是稠密性，整數集沒有這一特性，因為兩個相鄰的整數之間就沒有其他的整數了。
基本含義
有理數可分為整數和分數也可分為正有理數，0，負有理數。除了無限不循環小數以外的數統稱有理數。有理數（rationalnumber) 讀音:(yǒulǐshù)整數和分數統稱為有理數，任何一個有理數都可以寫成分數m/n（m，n都是整數，且n≠0）的形式。任何一個有理數都可以在數軸上表示。其中包括整數和通常所說的分數，此分數亦可表示為有限小數或無限循環小數。這一定義在數的十進制和其他進位制（如二進制）下都適用。數學上，有理數是一個整數a和一個非零整數b的比(ratio)，通常寫作a/b，故又稱作分數。希臘文稱為λογο?，原意為“成比例的數”(rationalnumber)，但中文翻譯不恰當，逐漸變成“有道理的數”。無限不循環小數稱之為無理數（例如：圓周率π）有理數和無理數統稱為實數。所有有理數的集合表示為Q。
包括內容
(1)自然數：數0，1，2，3，……叫做自然數.(2)正整數：＋1，＋2，＋3，……叫做正整數。(3）負整數：－1，－2，－3，……叫做負整數。(4）整數：正整數、0、
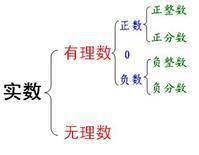有理數負整數統稱為整數。(5）分數：正分數、負分數統稱為分數。(6）奇數：不能被2整除的整數叫做奇數。如-3，-1，1，5等。所有的奇數都可用2n-1或2n+1表示，n為整數。(7）偶數：能被2整除的整數叫做偶數。如-2，0，4，8等。所有的偶數都可用2n表示，n為整數。(8）質數：如果一個大於1的整數，除了1和它本身外，沒有其他因數，這個數就稱為質數，又稱素數，如2，3，11，13等。2是最小的質數。(9）合數：如果一個大於1的整數，除了1和它本身外，還有其他因數，這個數就稱為合數，如4，6，9，15等。4是最小的合數。一個合數至少有3個因數。(10）互質數：如果兩個正整數，除了1以外沒有其他公因數，這兩個整數稱為互質數，如2和5，7和13等。……如3，-98.11，5.72727272……，7/22都是有理數。全體有理數構成一個集合，即有理數集，用粗體字母Q表示，較現代的一些數學書則用空心字母Q表示。有理數集是實數集的子集，即Q?R。相關的內容見數系的擴張。
運算定律
有理數集是一個域，即在其中可進行四則運算（0作除數除外），而且對於這些運算，以下的運算律成立（a、b、c等都表示任意的有理數）.①加法的交換律a+b=b+a；②加法的結合律a+(b+c)=(a+b)+c；③存在數0，使0+a=a+0=a；④乘法的交換律ab=ba；⑤乘法的結合律a(bc)=(ab)c；⑥乘法的分配律a(b+c)=ab+ac。0a＝0文字解釋：一個數乘0還等於0。此外，有理數是一個序域，即在其上存在一個次序關係≤。0的絕對值還是0.有理數還是一個阿基米德域，即對有理數a和b，a≥0，b>0，必可找到一個自然數n，使nb>a。由此不難推知，不存在最大的有理數。值得一提的是有理數的名稱。“有理數”這一名稱不免叫人費解，有理數並不比別的數更“有道理”。
產生
古埃及人約於公元前17世紀初已使用分數，中國《九章算術》中也載有分數的各種運算。分數的使用是由於除法運算的需要。除法運算可以看作求解方程px=q（p≠0），如果p，q是整數，則方程不一定有整數解。為了使它恆有解，就必須把整數系擴大成為有理系。事實上，這似乎是一個翻譯上的失誤。有理數一詞是從西方傳來，在英語中是（rationalnumber），而（rational）通常的意義是“理性的”。中國在近代翻譯西方科學著作，依據日語中的翻譯方法，以訛傳訛，把它譯成了“有理數”。但是，這個詞來源於古希臘，其英文詞根為（ratio），就是比率的意思（這裡的詞根是英語中的，希臘語意義與之相同）。所以這個詞的意義也很顯豁，就是整數的“比”。與之相對，而“無理數”就是不能精確表示為兩個整數之比的數，而並非沒有道理（無理數就是無限不循環小數，π也是其中一個無理數）。
運算
有理數加減混合運算。1.理數加減統一成加法的意義；對於加減混合運算中的減法，我們可以根據有理數減法法則將減法轉化為加法，這樣就可將混合運算統一為加法運算，統一後的算式是幾個正數或負數的和的形式，我們把這樣的式子叫做代數和。2.有理數加減混合運算的方法和步驟：（1）運用減法法則將有理數混合運算中的減法方程轉化為加法。（2）運用加法法則，加法交換律，加法結合律簡便運算。一般情況下，有理數是這樣分類的：整數、分數；正數、負數和零；負有理數，非負有理數。整數和分數統稱有理數,有理數可以用a/b的形式表達，其中a、b都是整數，且互質。我們日常經常使用有理數的。比如多少錢，多少斤等。凡是不能用a/b形式表達的實數就是無理數，又叫無限不循環小數。在有理數中，小數就是分數。
