拓撲群
正文
又名連續群,是具有拓撲空間結構的群。設G是拓撲空間，又是一個群，而且群的乘積運算與求逆按此拓撲是連續的，即從拓撲空間G×G到拓撲空間G上的映射m∶(x,y)→x·y及從G到G上的映射ƒ:x→x-1 都是連續映射，則稱G為拓撲群。如果G作為拓撲空間是局部緊(或緊、連通、單連通)的,則稱G為局部緊(或緊、連通、單連通)拓撲群。例如,n維歐氏空間中所有向量所成的加群，再加上通常的拓撲，就是一個交換拓撲群；實數域R上所有n階非奇異方陣所成的乘法群GL(n,R),再加上通常的拓撲，是一個局部緊拓撲群;而所有行列式為1的正交矩陣所成的群SO(n,R)是一個緊連通拓撲群。從拓撲群G到拓撲群H內的映射ƒ:G→H,如果作為群結構它是群同態，作為拓撲空間的映射它是連續的，那么ƒ稱為從拓撲群G到拓撲群H的同態，簡稱同態。如果同態ƒ是雙射, 而且逆映射ƒ-1也是連續的，那么ƒ稱為拓撲群G到拓撲群H上的同構映射，簡稱同構。拓撲群全體帶上拓撲群間的同態，構成一個範疇。這個範疇就是拓撲群論研究的對象。
在數學中，拓撲群概念最初是由連續變換群的研究所引起，人們發現在處理許多連續變換群的問題中所出現的群，往往不必考慮作變換群，而只需研究這些群本身，於是產生了連續群的概念。M.S.李是最初對連續群進行系統研究而卓有成就的人。李群就是因他得名。
拓撲群的結構是比較均勻的，一點鄰近的性質可以反映其他點鄰近的性質。設G為群,
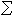
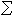
為G的某些子集構成的集合。如果 適合下列五個條件：①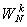
，其中e為G的單位元素；②對U、V∈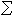,存在W ∈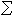使W嶅U ∩V;③對每個U ∈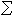,存在V∈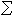使VV-1嶅U;④對每個U∈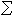及α∈U，存在V∈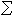使Vα嶅U；⑤對每個U∈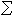及α∈G,存在V∈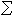使α-1Vα嶅U,那么在G中可以引進惟一的拓撲,以{Uα｜U∈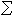,α∈G},為拓撲空間的完全鄰域組，使G成為拓撲群，亦即拓撲群G的拓撲結構完全決定於單位的完全鄰域組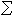,只要拓撲群中有一點是閉集,那么每一點都是閉集,從而是豪斯多夫空間，並且這樣的拓撲群的拓撲空間是正則的。連通拓撲群作為抽象群都可以由它的單位的一個鄰域來生成。 如果拓撲群G的子集H是群G的子群,那么H加上由G的拓撲繼承下來的拓撲也構成拓撲群，就稱H為拓撲群G的拓撲子群；如果H 又是G 的閉（開）子集，那么H 稱為G 的閉(開)子群。開子群一定是閉子群。拓撲群G 的子群H 的閉包啛 也是拓撲子群。拓撲群G 的中心與換位子群都是G 的閉正規子群。給出拓撲群G 的子群H,就可以有左陪集的集合G/H ={αH丨α∈G},有從G 到G/H上的自然映射π∶G→G/H,π(α)=αH,對α∈G,G/H上使π連續的最強拓撲，使G/H成拓撲空間，稱為G關於子群H 的左陪集空間。同樣有右陪集空間H\G。於是, G/H是豪斯多夫空間若且唯若H是閉子群。G/H是離散的,若且唯若H是開子群。如果H是拓撲群G 的正規子群，那么商群G/H再加上上述陪集空間拓撲，使G/H成拓撲群，稱為拓撲群G按正規子群H所做得的商群。這時，從拓撲群G到拓撲群G/H的自然映射 π是拓撲群間的開同態（作為拓撲空間的映射把開集映到開集）。還有類似於群同態基本定理的同態定理：如果ƒ是從拓撲群G到拓撲群G1上的開同態映射，N為ƒ的核,那么N是G的閉正規子群，而且由ƒ導出G/N到G1上的映射是拓撲群間的同構映射。
在研究拓撲群的結構及討論拓撲群上函式的性質時，一個非常重要的有力工具是,在局部緊拓撲群G上可以建立起不變測度與不變積分，即G 有一個適當廣的可測子集類（博雷爾子集類）,在這個類集上可以有一個測度μ，使得對G中的任一元素α，可測集M的測度μ(M)與集合Mα的測度μ(Mα)相等。這種測度稱為局部緊群G上的哈爾測度。它是A.哈爾於1933年首先建立起來的理論。 可以證明, 除了一個常數因子外，局部緊群上的哈爾測度是惟一確定的。緊子集上的哈爾測度是有限的，因此, 在緊群G上哈爾測度總可以標準化為μ(G)=1。有了測度就可以在局部緊拓撲群上建立起不變積分的理論。1934年J.馮·諾伊曼用比A.哈爾簡單得多的方法，在緊群上直接建立起不變積分的理論。早在1927年,F.彼得與（C.H.）H.外爾已經在討論緊李群的線性表示時用到了不變積分。
拓撲群的表示理論也是研究拓撲群的一個重要方面。從拓撲群G到所有n階非奇異方陣所成的拓撲群GL(n,C)中的同態,稱為G的一個線性表示。與有限群的線性表示理論相似，緊拓撲群的線性表示也具有完全可約性、正交性、完備性。所謂完全可約性，是指緊拓撲群的任一線性表示都是不可約表示的直和。所謂正交性，是指緊群G 的任意兩個維數各為m與n的不等價的不可約表示ρ 與σ,ρ:x→ρ(x)=(gij(x)),x∈G,i,j=1,2,…,m;σ:x→σ(x)＝(hkl(x))，x∈G，k，l＝1,2,…, n，有關係式
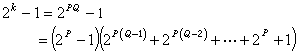
，當i≠s或j≠t時;式中積分是群G上的不變積分, 抧ij(x)、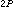
(x)分別是gij(x)、
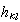(x)的共軛。 所謂完備性,是指如果Ω表示緊群G的所有不可約表示中所出現的連續函式gij(x)全體，那么G上任一連續函式都可用Ω中函式的線性組合來逼近。這就是著名的彼得－外爾定理。
在拓撲群中研究得最多的是局部歐氏群。當拓撲群G的某一點有鄰域同胚於歐氏空間的開集，則G稱為局部歐氏群。許多數學家在研究希爾伯特第 5問題即是否每一個局部歐氏群都是李群時作出了貢獻。Л.C.龐特里亞金於1934年解決了交換群的情況，馮·諾伊曼解決了緊群的情況，D.蒙哥馬利和L.齊平證明了任一局部連通的有限維的局部緊群是李群，從而肯定了D.希爾伯特的猜測。
拓撲群的理論是李群的基礎。李群在數學的許多方面有廣泛的聯繫，在物理學中有大量的套用。
