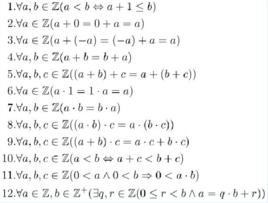概述
實數公理是在集合論發展的基礎上,由希爾伯特於1899年首次提出的。後來他所提的公理系統在相容性與獨立性方面得到了進一步改進,逐步演變為現在的公理系統。 實數公理來源於實數理論的研究,實數理論包括對實數的結構,運算法則和拓撲性質等方面問題的研究。
實數集有多重結構,例如:
代數結構:從代數上看實數集是一個域。
序結構:實數集是一個有序集。
拓撲結構:實數集是一個拓撲空間,並且有諸如完備性,可分性,和列緊性等一些非常好的性質。
實數理論包含了深刻而豐富的信息,實數理論是極限論的基礎,也是近代分析數學的最重要基礎之一。
實數系的公理系統
設 R是一個集合,若它滿足下列三組公理,則稱為 實數系,它的元素稱為 實數:
(I) 域公理
對任意a,b∈R,有R中惟一的元素a+b與惟一的元素a·b分別與之對應,依次稱為a,b的 和與 積,滿足:
1.(交換律) 對任意a,b∈R,有
a+b=b+a,a·b=b·a。
2.(結合律) 對任意a,b,c∈R,有
a+(b+c)=(a+b)+c,a·(b·c)=(a·b)·c。
3.(分配律) 對任意a,b,c∈R,有
(a+b)·c=a·c+b·c。
4.(單位元) 存在R中兩個不同的元素,記為0,1分別稱為 加法單位元與 乘法單位元,使對所有的a∈R,有
a+0= a,a·1=a。
5.(逆元) 對每個a∈R,存在R中惟一的元素,記為-a,稱為 加法逆元;對每個a∈R\{0},存在R中惟一的元素,記為a^(-1),稱為 乘法 逆元,使
a+(-a)=0。a·a^(-1)=1。
(II) 序公理
(a)
在任意兩個元素a,b∈R之間存在一種關係,記為“>”,使對任意a,b,c∈R,滿足:
1.(三歧性) a>b,b>a,a=b三種關係中必有一個且僅有一個成立。
2.(傳遞性) 若a>b且b>c則a>c。
3.(與運算的相容性) 若a>b,則a+c>b+c;若a>b,c>0則ac>bc。
(b)
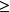 實數公理
實數公理在任意兩個元素a,b∈R之間存在一種關係,記為“”,使對任意a,b,c∈R,滿足:
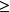 實數公理
實數公理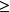 實數公理
實數公理1.(反對稱性) 若ab且,ba那么a=b。
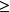 實數公理
實數公理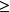 實數公理
實數公理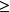 實數公理
實數公理2.(傳遞性) 若ab且bc則ac。
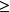 實數公理
實數公理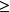 實數公理
實數公理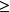 實數公理
實數公理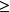 實數公理
實數公理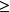 實數公理
實數公理3.(與運算的相容性) 若ab,則a+cb+c;若a0且b0,則ab0。
註:對於序公理a,b這兩種描述是等價的。因為我們可以通過其中一個符號及其性質來定義另一個符號。
(III)(1) 阿基米德公理(也稱阿基米德性質,它並不是嚴格意義上的公理,可以由連續性公理證明。在歐幾里得的幾何書中,它僅被描述為一個命題 )。
阿基米德公理:對任意a,b∈R,a>0 存在正整數n,使na>b。
(III)(2)完備性公理
R中的任何基本列都在R中收斂。
稱滿足公理組 I的集為 域;滿足公理組 I與 II的集為 有序域;滿足公理組 I, II與(III)(1)的集為 阿基米德有序域;滿足公理組 I~ III的集為 完備阿基米德有序域或 完備有序域。這樣,實數系就是完備阿基米德有序域。所有有理數的集合Q就是阿基米德有序域,但它不滿足完備性公理。根據域公理,可以定義實數的減法和除法,並證明四則運算的所有性質。序公理的1與2表明關係“>”是R的全序。
用域公理和序公理可以定義正數、負數、不等式、絕對值,並證明它們具有通常的運算性質。加上阿基米德公理與完備性公理,可以證明實數的其他性質以及冪、方根、對數等的存在性。實數公理有多種不同的提法,常見的另一種提法是把公理組 III換成
(III)’連續性公理(戴德金公理)
若A,B是R的非空子集且 A∪B=R ,又對任意的x∈A 及任意的 y∈B 恆有x<y,則A有最大元或B有最小元,即存在 c∈R,使 x<c<y。
這裡把戴德金定理用作連續性公理。另一個常用作連續性公理的確界原理。公理組 I~ III與公理組 I+ II+ (III)’是等價的,(注意不是 III<=>(III)’)。完備性公理可以換成閉區間套定理的形式。類似地,單調收斂定理,聚點原理等也可用作連續性公理。公理組 II也有其他提法。用公理定義了實數系 R後,可以繼續定義R的特殊元素正整數、整數等。例如,由數1生成的子加群 Z={0,±1,±2,…}的元素稱為 整數;由數1生成的子域 Q={p/q|p,q∈Z,q≠0}的元素稱為 有理數。
但這裡有一個很微妙的問題,即與連續性公理等價的7個實數系的基本定理(確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和柯西收斂準則)中,並不是每一個都能推出阿基米德公理的。具體來說,柯西收斂準則和閉區間套定理就是如此,其他5個基本定理則可以推出阿基米德公理。因此,以連續性公理作為實數公理之一時,阿基米德公理可以去掉,這時連續性和完備性是統一的,所以連續性公理也可以稱為完備性公理;而以柯西收斂準則或閉區間套定理代替連續性公理時,連續性和完備性是分離的,必須補充阿基米德公理,這時柯西收斂準則或比區間套定理就只能稱為完備性公理,是為了公理的完備而存在的。
滿足這些公理的任何集合R,都可被認為是實數集的具體實現,或稱為 實數模型。 需要說明的是,實數公理下的系統是相容的,範疇的。
從另外一個角度來想,希爾伯特實數公理是自上而下建立數系的,用公理規定實數,然後再定義整數、正整數直至自然數。那么反過來行不行呢,實數的這些公理能不能從其他的假設中推出來呢,事實上,這就是實數的構造理論所做的事了,在菲赫金哥爾茨的《微積分學教程》的緒論中,就展示了用戴德金分割的方法從有理數定義無理數的過程,從而建立了實數,而有理數是依賴於先建立整數的,整數又是依賴於先建立自然數的,當集合論發展起來之後,自然數又依靠集合來定義了(即皮亞諾公理),集合是最原始的概念,無法再定義的概念,整個自下而上的過程可以參見蘭道的《分析基礎》,從此,整個數學的基礎就建立在了集合論之上,數學再也不能排除掉集合這一現代概念了,當英國數學家羅素髮現了集合中的羅素悖論之後,引發了第三次數學危機,促使集合論又不得不加以改進,致使樸素集合論發展為近代集合論,現代的數學基礎終於建立在了公理集合論的基礎之上(ZFC公理系統)。
實數模型
一、戴德金分割(分劃)模型
二、柯西數列模型
三、魏爾斯特拉斯十進制小數模型
四、康托爾閉區間套模型(可歸入第三個模型)
實數的基本定理
實數系的基本定理也稱實數系的完備性定理、實數系的連續性定理,這些定理分別是確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和柯西收斂準則,共7個定理,它們彼此等價,以不同的形式刻畫了實數的連續性,它們同時也是解決數學分析中一些理論問題的重要工具,在微積分學的各個定理中處於基礎的地位。7個基本定理的相互等價不能說明它們都成立,只能說明它們同時成立或同時不成立,這就需要有更基本的定理來證明其中之一成立,從而說明它們同時都成立,引進方式主要是承認戴德金公理,然後證明這7個基本定理與之等價,以此為出發點開始建立微積分學的一系列概念和定理。在一些論文中也有一些新的等價定理出現,但這7個定理是教學中常見的基本定理。
一、上(下)確界原理
非空有上(下)界數集必有上(下)確界。
二、單調有界定理
單調有界數列必有極限。具體來說:
單調增(減)有上(下)界數列必收斂。
三、閉區間套定理(柯西-康托爾定理)
對於任何閉區間套,必存在屬於所有閉區間的公共點。若區間長度趨於零,則該點是唯一公共點。
四、有限覆蓋定理(博雷爾-勒貝格定理,海涅-波雷爾定理)
閉區間上的任意開覆蓋,必有有限子覆蓋。或者說:閉區間上的任意一個開覆蓋,必可從中取出有限個開區間來覆蓋這個閉區間。
五、極限點定理(波爾查諾-魏爾斯特拉斯定理、聚點定理)
有界無限點集必有聚點。或者說:每個無窮有界集至少有一個極限點。
六、有界閉區間的序列緊性(緻密性定理)
有界數列必有收斂子列。
七、完備性(柯西收斂準則)
數列收斂的充要條件是其為柯西列。或者說:柯西列必收斂,收斂數列必為柯西列。
註:只有充要條件的命題才能稱之為“準則”,否則不能稱為“準則”。
以上7個命題稱為 實數系的基本定理。實數系的7個基本定理以不同形式刻畫了實數的連續性,它們彼此等價。在證明中,可採用單循環證明的方式證明它們的等價性。它們之間等價性的證明可以參看《數學分析札記》。
在閉區間上連續函式的性質的證明中,實數系的基本定理是非常重要的工具,但是它們之間的等價性不能說明它們都成立,必須要有更基本的定理來證明其中之一成立,從而以上的命題都成立,進過反覆仔細琢磨,問題就歸結為實數的引入問題了。如在菲赫金哥爾茨的《微積分學教程》 中,可以用實數的連續性來推出確界定理,在華東師範大學數學系編的《數學分析(上冊)》(第四版)中就通過實數十進制小數形式推出確界定理,這也說明了建立實數系的嚴格定義的重要性。從邏輯上,應該是先建立了實數,有了實數的定義之後,再得出實數系的基本定理,從而能夠在實數域上建立起嚴格的極限理論,最後得到嚴格的微積分理論,但數學歷史的發展恰恰相反,最先產生的是微積分理論,而嚴格的極限理論是在19世紀初才開始建立的,實數系的基本定理已經基本形成了之後,19世紀末實數理論才誕生,這時分析的算數化運動才大致完成。