簡介
完全數（Perfectnumber），又稱完美數或完備數，是一些特殊的自然數。它所有的真因子（即除了自身以外的約數）的和（即因子函式），恰好等於它本身。概述
概念定義各個真約數的和等於它本身的自然數叫做數完全（Perfectnumber），又稱完美數或完備數。（列出某數的約數，去掉該數本身，剩下的就是它的真約數）
舉例
例如：第一個完全數是6，它有約數1、2、3、6，除去它本身6外，其餘3個數相加，1+2+3=6。第二個完全數是28，它有約數1、2、4、7、14、28，除去它本身28外，其餘5個數相加，1+2+4+7+14=28。後面的完全數還有496、8128等等。
相關概念
對於“4”這個數，它的真約數有1、2，其和是3，比4本身小，像這樣的自然數叫做虧數。對於“12”這個數，它的真約數有1、2、3、4、6，其和是16，比12本身大，像這樣的自然數叫做盈數。所以，完全數就是既不盈餘，也不虧欠的自然數。
性質
完全數有許多有趣的性質：1、它們都能寫成連續自然數之和（三角形數） 例如：6=1+2+3
28=1+2+3+4+5+6+7
496=1+2+3+……+30+312、每個都是調和數
它們的全部因數的倒數之和都是2，因此每個完全數都是調和數。例如：
1/1+1/2+1/3+1/6=2
1/1+1/2+1/4+1/7+1/14+1/28=23、可以表示成連續奇立方數之和
除6以外的完全數，還可以表示成連續奇立方數之和。例如：
28=1^3+3^3
496=1^3+3^3+5^3+7^3
8128=1^3+3^3+5^3+……+15^3
33550336=1^3+3^3+5^3+……+125^3+127^34、都可以表達為2的一些連續正整數次冪之和
例如：
6=2^1+2^2
28=2^2+2^3+2^4
8128=2^6+2^7+2^8+2^9+2^10+2^11+2^12
33550336=2^12+2^13+……+2^245、完全數都是以6或8結尾
如果以8結尾，那么就肯定是以28結尾。6、各位數字相加直到變成個位數則一定是1
除6以外的完全數，把它的各位數字相加，直到變成個位數，那么這個個位數一定是1。（亦即：除6以外的完全數，被9除都餘1）
28：2+8=10，1+0=1
496：4+9+6=19，1+9=10，1+0=1
發現
古希臘數學家歐幾里得是通過2n−1(2n−1)的表達式發現頭四個完全數的。當n=2:21(22−1)=6當n=3:22(23−1)=28當n=5:24(25−1)=496
當n=7:26(27−1)=8128
一個偶數是完美數，若且唯若它具有如下形式：2n−1(2n−1)，此事實的充分性由歐幾里得證明，而必要性則由歐拉所證明。
其中2n−1是素數，上面的6和28對應著n=2和3的情況。我們只要找到了一個形如2n−1的素數（即梅森素數），也就知道了一個偶完美數。
儘管沒有發現奇完全數，但是當代數學家奧斯丁·歐爾證明，若有奇完全數，則其形式必然是12p+1或36p+9的形式，其中p是素數。在1018以下的自然數中奇完全數是不存在的。
首十個完全數是：
628496812833550336(8位)8589869056(10位)137438691328(12位)2305843008139952128(19位)2658455991569831744654692615953842176(38位)191561942608236107294793378084303638130997321548169216(55位)
歷史
畢達哥拉斯完全誕生後，吸引著眾多數學家與業餘愛好者像淘金一樣去尋找。它很久以來就一直對數學家和業餘愛好者有著一種特別的吸引力，他們沒完沒了地找尋這一類數字。接下去的兩個完數看來是公元1世紀，畢達哥拉斯學派成員尼克馬修斯發現的，他在其《數論》一書中有一段話如下：也許是這樣，正如美的、卓絕的東西是罕有的，是容易計數的，而醜的數論、壞的東西卻滋蔓不已；是以盈數和虧數非常之多，雜亂無章，它們的發現也毫無系統。但是完全數則易於計數，而且又順理成章：因為在個位數里只有一個6；十位數里也只有一個28；第三個在百位數的深處，是496；第四個卻在千位數的尾巴上，接近一萬，是8128。它們具有一致的特性：尾數都是6或8，而且永遠是偶數。第五個完全數要大得多，是33550336，它的尋求之路也艱難得多，直到十五世紀才由一位無名氏給出。這一尋找完全數的努力從來沒有停止。電子計算機問世後，人們藉助這一有力的工具繼續探索。笛卡爾曾公開預言：“能找出完全數是不會多的，好比人類一樣，要找一個完美人亦非易事。”時至今日，人們一直沒有發現有奇完全數的存在。於是是否存在奇完全數成為數論中的一大難題。目前，只知道即便有，這個數也是非常之大，並且需要滿足一系列苛刻的條件。
梅森素數
古希臘數學家歐幾里得在名著《幾何原本》中證明了素數有無窮多個，並論述完全數時提出：如果2^P-1是素數(其中指數P也是素數)，則2^(P-1)(2^P-1)是完全數。瑞士數學家和物理學家歐拉證明所有的偶完全數都有這種形式。因此，人們只要找到2^P-1型素數，就可以發現偶完全數了。數學界將2^P-1型素數稱為“梅森素數”(Mersenneprime)，因為法國數學家和法蘭西科學院奠基人梅森在這方面的研究成果較為卓著。梅森素數貌似簡單，但探究難度卻極大。它不僅需要高深的理論和純熟的技巧，而且還需要進行艱巨的計算。到2013年2月6日為止，人類僅發現48個梅森素數。值得提出的是：在梅森素數的基礎研究方面，法國數學家魯卡斯和美國數學家雷默都做出了重要貢獻；以他們命名的“魯卡斯-雷默方法”是目前已知的檢測梅森素數素性的最佳方法。此外，中國數學家和語言學家周海中給出了梅森素數分布的精確表達式，為人們尋找梅森素數提供了方便；這一研究成果被國際上命名為“周氏猜測”。
其他介紹
一個正整數n,其全部因數的和等於2n。例如6的因數的和是1+2+3+6=12，28的因數的和是1+2+4+7+14+28=56，所以6與28都是完全數(也稱完美數)。公元前6世紀，古希臘數學家畢達哥拉斯,就首先觸及完全數問題。古希臘數學家歐幾里得證明了p和2 -1均為素數時，2 (2 -1)是一個完全數,為此而初步建立了整數的可除性理論。約二千年之後,L.歐拉證明了每一個偶完全數n都具有歐幾里得指出的形狀,即n=2 (2 -1)，這裡p和2 -1均為素數。1911年,L.E.迪克森給出上述結果一個簡短的證明。由此可見，偶完全數與梅森數2 -1有密切關係。完全數非常稀少，至今人們只發現47個，而且都是偶完全數。前5個完美數分別是：6，28，496，8128，33550336。
否有無窮多個偶完全數的問題，歸結為是否有無窮多個素數p使2 -1是素數,這是數論中尚未解決的著名問題。是否存在奇完全數，是完全數中另一個著名難題，儘管有許多數學家進行了大量的工作，但至今仍未解決。L.歐拉曾經證明，奇完全數n如果存在，則n的分解式為
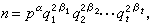(*)式中p,q1,q2,…，qt是不同的素數，α 呏p 呏1(mod4)。1888年，J.J.西爾維斯特證明了t≥4,他還指出了t=4不可能。1970年，W. 麥克丹尼爾證明了（*）中2βj+1呏0(mod3)(j=1,2,…,t)。1973年,P.哈吉斯證明了如果n是奇完全數，那么n>10 。1978年，有人證明了若n為奇完全數，則
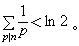1980年，哈吉斯還證明了如果存在奇完全數n，則n至少有8個不同的素因子。相關內容
一、偶完全數定理：若p=2n-1為素數，則
p(p+1)=2的n次冪×(2的n次冪-1) 是一個偶完全數
1.因為p(p+1) 是二個連續數必有一個是偶數，所以它是一個偶完全數定理。
2.華羅庚《數論導引》中說明了此公式與梅森數的關係：有一個梅森數就有一個偶完全數。並有證明在二個連續的梅森數之間不存在偶完全數。
3.古希臘數學家歐幾里得在名著《幾何原本》中證明了素數有無窮多個，並論述完全數時提出：如果2^P-1是素數(其中指數P也是素數)，則2^(P-1)(2^P-1)是完全數。瑞士數學家和物理學家歐拉證明所有的偶完全數都有這種形式。因此，人們只要找到2^P-1型素數，就可以發現偶完全數了。數學界將2^P-1型素數稱為“梅森素數”(Mersenneprime)，因為法國數學家和法蘭西科學院奠基人梅森在這方面的研究成果較為卓著。梅森素數貌似簡單，但探究難度卻極大。它不僅需要高深的理論和純熟的技巧，而且還需要進行艱巨的計算。迄今為止，人類僅發現47個梅森素數。
值得提出的是：在梅森素數的基礎研究方面，法國數學家魯卡斯和美國數學家雷默都做出了重要貢獻；以他們命名的“魯卡斯-雷默方法”是目前已知的檢測梅森素數素性的最佳方法。此外，中國數學家和語言學家周海中給出了梅森素數分布的精確表達式，為人們尋找梅森素數提供了方便；這一研究成果被國際上命名為“周氏猜測”。
二、奇完全數推導
命題一：奇完全數必含奇次方的素因數。
證明：由2n=因數和，可知n=真因數和。(真因數和是指不含n的因數）
例如:2ab=1+a+b+ab(因數和) ,
ab=1+a+b(真因數和)
設a,b為奇素數
（1）n=aabb型含有因數
a
aa
b ab aab
bb abb
aabb=a+aa+b+bb+ab+abb+aab
∵1+7個奇數=偶數，而aabb=奇數，∴無奇完全數。
（2）n=aaaabb型含有因數
a
aa
aaa
aaaa
b ab aab aaab aaaab
bb abb aabb aaabb
∵1+13個奇數=偶數，∴無奇完全數
由此可見，a的偶次方乘b的偶次方無奇完全數.
（3）aaBBCC 型無奇完全數
abbcc bbcc aABCC aacc aabbc aabb
a abcc acc abbc
aa bcc bbc
b ab aab AABC
bb abb bc
c ac aac
cc abc
∵1+25個奇數=偶數，∴無奇完全數。
因此奇完全數必含有奇次方的因子。
命題2.若存在奇完全數，則必有（pi的a+1次方-1）/（pi-1)/2=奇數或非整數的奇素數組成。
證明：定理：σ(n)=∏（pi的ai+1-1）/（pi-1）
又∵有奇完全數定義知：σ(n)=2n ，n為奇素數之積。
∴σ(n)/2=n=奇數積
又∵偶數×奇數=偶數
∴（pi的a+1次方-1）/（pi-1）/2=奇數或非整數。
三。不存在一次方的奇完全數。
證明：
（1）σ(pq）=1+p+q+pq=(p+1)(q+1)
∵p,q為奇素數,∴（p+1),(q+1)均為偶數。（p+1)(q+1)=2²（p+1)/2×(q+1)/2
∵σ(n)=2n=2×奇數≠2×偶數。∴不存在二個因數一次方的奇完全數。
（2）σ(pqr)=1+p+q+r+pq+pr+qr+pqr=(p+1)(q+1)(r+1)=2³(p+1)/2×(q+1)/2×(r+1)/2
所以三個因數同樣沒有一次方的奇完全數。
(3)σ（p1p2.....pn)=(p1+1)(p2+1)....(pn+1)=2的n次方（p1+1)/2×(p2+1)/2×.....×(pn+1)/2
故不存在n個因數一次方的奇完全數。
四。不存在純奇次的奇完全數。
∵當a 為奇數時，[p的(a+1)次方-1]/(p-1)=偶數。故與三。有相同的結果。
五。綜上所述，若存在奇完全數n則
n=p的α次方×q1的2β次方×q2的2γ次方×....×qn的2θ次方
注1：.p的a次方必須是（p的α+1次方-1)/(p-1)=2×奇數，
故：a≠3
當a=1,5時，p≠3,7,11,19,23,31,43,47,59,...
p可以是5,13,17,29,37,41,53,....
注2：q1,q2,..qn為不同的奇素數。且(q的2m+1次方-1)/(q-1)為奇數。推畢。
趣味數學
| 趣味數學以帶有強烈的遊戲色彩知名於世。歐拉就是通過對bridge-crossing之謎的分析打下了拓撲學的基礎。萊布尼茨也寫到過他在獨自玩插棍遊戲時分析問題的樂趣。希爾伯特證明了切割幾何圖形中的許多重要定理。馮·紐曼奠基了博弈論。最受大眾歡迎的計算機遊戲—生命是英國著名數學家康威發明的。愛因斯坦也收藏了整整一書架關於數學遊戲和數學謎的書。 |
